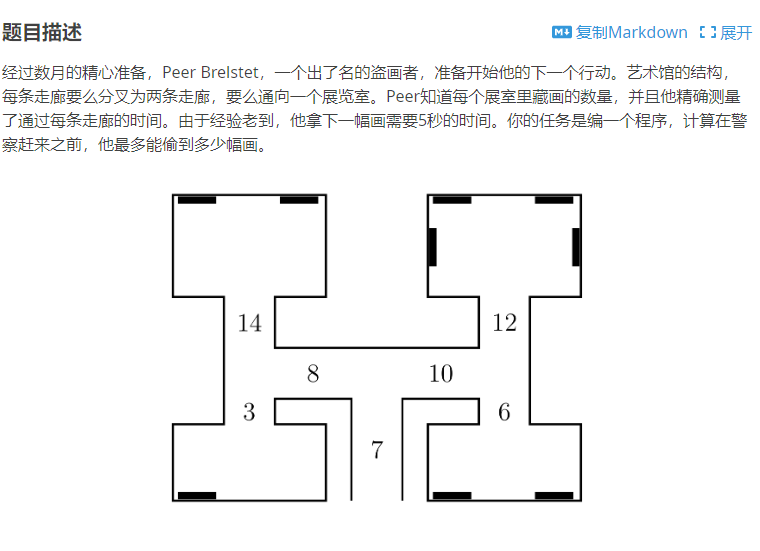
题意
注意:
- 要预留一秒的时间!!!不然你就 80 pts 分了。
- 小偷要回到大门。
思路
定义 \(f_{i, j}\) 表示到在 \(i\) 的子树内拿 \(j\) 幅画。
那么我们可以枚举 \(f_{to, k}\) 表示在儿子结点拿 \(k\),那么总共为 \(f_{u, j + k} = min(f_{u, j + k}, f_{u, j} + f_{to, k} + 2w)\)。
我们为了防止 \(f\) 被反复利用,变成了左脚踩右脚上天,所以我们每次转移的时候定义临时数组,然后后面再 copy 回来。
代码
#include <bits/stdc++.h>using namespace std;const int N = 810, M = 2010, INF = 0x3f3f3f3f;struct edge {int to, next, w;
} e[N];int head[N], idx = 1;void add(int u, int v, int w) {idx++, e[idx].to = v, e[idx].w = w, e[idx].next = head[u], head[u] = idx;
}int atime, n, cnt[N], sum;void input(int u) {int w, c;cin >> w >> c;add(u, ++n, w);int rt = n;if (!c) {input(rt);input(rt);}else {cnt[n] = c;sum += c;}
}int f[N][M], g[M];void dfs(int u, int fa) {if (cnt[u]) {for (int j = 0; j <= cnt[u]; j++) {f[u][j] = j * 5;}return;}f[u][0] = 0;for (int i = head[u]; i; i = e[i].next) {int to = e[i].to;if (to == fa) continue;dfs(to, u);memcpy(g, f[u], sizeof(g));for (int j = 0; j <= sum; j++) {for (int k = 1; j + k <= sum; k++) {g[j + k] = min(g[j + k], f[u][j] + f[to][k] + 2 * e[i].w);}}memcpy(f[u], g, sizeof(g));}
}int main() { ios::sync_with_stdio(false);cin.tie(nullptr);cin >> atime;input(++n);memset(f, 0x3f, sizeof(f));dfs(1, 0);int lst = 0;for (int i = 0; i <= sum; i++) {if (f[1][i] < atime) {lst = i;}}cout << lst << '\n';return 0;
}