EPIC Institute of Technology Round August 2024 (Div. 1 + Div. 2) 补题记录（A~D1，E）

A

容易发现答案为 \(\min(n,k)\min(m,k)\)。

#include<bits/stdc++.h>
#define int long long
#define pb push_back
using namespace std;
const int N=1000100;
int a[N];
signed main(){int T;cin>>T;while(T--){int n,m,k;cin>>n>>m>>k;n=min(n,k),m=min(m,k);cout<<n*m<<'\n';}return 0;
} // main

B

容易发现 Alice 如果想要赢必然一直从左或者右端口开始删除元素。若对于 Alice 两种选择方案 Bob 都能够获胜那么 Bob 就必胜，反之 Bob 必败。用一个双端队列维护 Bob 当前所有的元素即可，时间复杂度为 \(O(n)\)。

#include<bits/stdc++.h>
#define int long long
#define pb push_back
using namespace std;
const int N=1000100;
int a[N],b[N];
signed main(){int T;cin>>T;while(T--){int n;cin>>n;for(int i=1;i<=n;++i)cin>>a[i];for(int i=1;i<=n;++i)cin>>b[i];deque<int>t;for(int i=1;i<=n;++i)t.push_back(b[i]);int ok=1;for(int i=1;i<=n;++i){if(a[i]==t.front())t.pop_front();else if(a[i]==t.back())t.pop_back();else{ok=0;break;}}reverse(a+1,a+n+1);for(int i=1;i<=n;++i)t.push_back(b[i]);for(int i=1;i<=n;++i){if(a[i]==t.front())t.pop_front();else if(a[i]==t.back())t.pop_back();else{ok=0;break;}}if(!ok)cout<<"Alice\n";else cout<<"Bob\n";}return 0;
} // main

C

谢谢你 C。考虑对于经过两点的直线 \(L\) 经过 \((x_1,y_1)\) 和 \((x_2,y_2)\)，对于一个圆心为 \((x_0,y_0)\) 的圆，若在某一个时刻 \(r\) 满足半径为 \(r\) 的圆和直线 \(L\) 距离 \((x_1,y_1)\) \(r\) 个单位长度的地方相交，则不可以经过。问题是如何判定这一点。

容易发现若 C –> D 的路径上 B 点和 A 点所对应的圆产生交点，则连接 \(AC\) 之后根据三角形三边关系得到 \(AD<CD\)，也就是从 \(C\) 走到 \(D\) 要花费的时间比圆半径从 \(A\) 扩展到 \(D\) 所需要的时间要长。

于是问题就十分简单了，只需要判断到达终点的时候是否有一个圆已经将终点覆盖即可。时间复杂度为 \(O(n)\)。

#include<bits/stdc++.h>
#define int long long
#define pb push_back
using namespace std;
const int N=331080;
int x[N],y[N];
int get(int a,int b,int c,int d){return (c-a)*(c-a)+(d-b)*(d-b);
}
signed main(){ios_base::sync_with_stdio(0);cin.tie(0);int T;cin>>T;while(T--){int n;cin>>n;for(int i=1;i<=n;++i)cin>>x[i]>>y[i];int xs,ys,xt,yt;cin>>xs>>ys>>xt>>yt;int ok=1;int len=get(xs,ys,xt,yt);for(int i=1;i<=n;++i){int len1=get(x[i],y[i],xt,yt);;if(len1<=len){ok=0;break;}}if(ok)cout<<"Yes\n";else cout<<"No\n";}return 0;
} // main
/*
1
1
999999998 1000000000
999999999 999999999 1 1
*/

D1

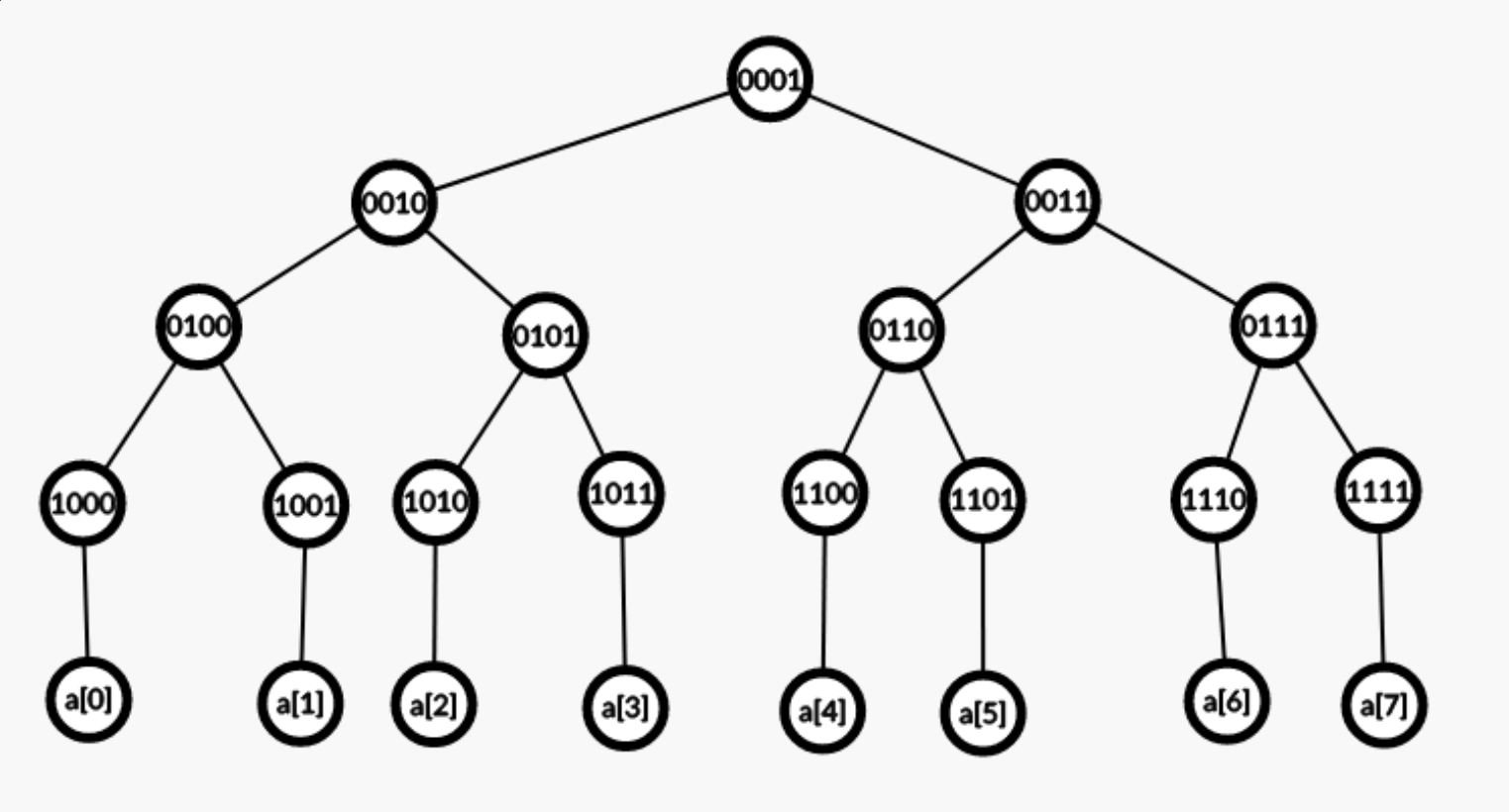
考虑维护 \(2\)、\(3\) 两个结点所对应的子树的结点编号的和，以及每一层树上结点编号的和，将其和真正的答案对比若相同就合法否则就不合法。时间复杂度为 \(O(n\log n)\)，需要使用 ds 维护。正确性显然。代码还没调出来。

E

这题还挺有意思的。考虑挖掘题目所求答案的性质，可以发现对于两个相邻的位置 \(i\)，\(i+1\) 所对应的连续二元组，若两个连续二元组所对应的值不同且第一个二元组的元素个数 \(\le\) 第二个二元组的元素个数那么第一个二元组的元素一定会被第二个二元组全部消除，随后第二个二元组的元素数量减去第一个二元组的元素数量。因此发现这个东西十分类似于单调栈。直接用单调栈维护一下当前的递减个数二元组即可。当前所需要花费的最长时间即为栈底元素最多的二元组的元素个数。

时间复杂度为 \(O(n)\)。感觉这个题比 C 和 D 都要简单啊。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=500100;
int a[N],b[N],res[N];
signed main(){int T;cin>>T;while(T--){int n;cin>>n;for(int i=1;i<=n;++i)cin>>a[i]>>b[i];deque<int> stk;int remain=0;for(int i=1;i<=n;++i){while(stk.size()){if(b[i]!=b[stk.back()]){if(a[i]>a[stk.back()])remain=a[stk.back()],stk.pop_back();else break;}else{a[i]+=a[stk.back()]-remain;stk.pop_back();remain=0;}}stk.push_back(i);cout<<a[stk.front()]<<' ';}cout<<'\n';}return 0;
}