第一眼是想写 \(kd-tree\) 的。
然后发现这就是一道三维前缀和的板子题。
三维前缀和
要想学习三维前缀和,我们首先得了解前缀和的概念,并且学会一维、二维前缀和。
什么是前缀和
前缀和是容斥原理的典型应用。这种优化方式可以使求和操作的时间复杂度降低到 \(O(1)\)(但是需要提前预处理)。
一维前缀和 & 二维前缀和
对于一维的一个序列 \(a_i\),如果我们有很多询问,每次询问让你求一个区间 \([l,r]\) 的和,我们就可以使用一维前缀和来优化。
具体地,我们设前缀序列 \(g_i = g_{i-1} + a_i\),那么不难发现,区间 \([l, r]\) 的和就是 \(g_r - g_{l - 1}\)。
对于一个二维的序列同理,我们设 \(g_{i,j} = g_{i-1,j} + g_{i,j-1} - g_{i-1,j-1} + a_{i,j}\),就可以求出任意部分的和。
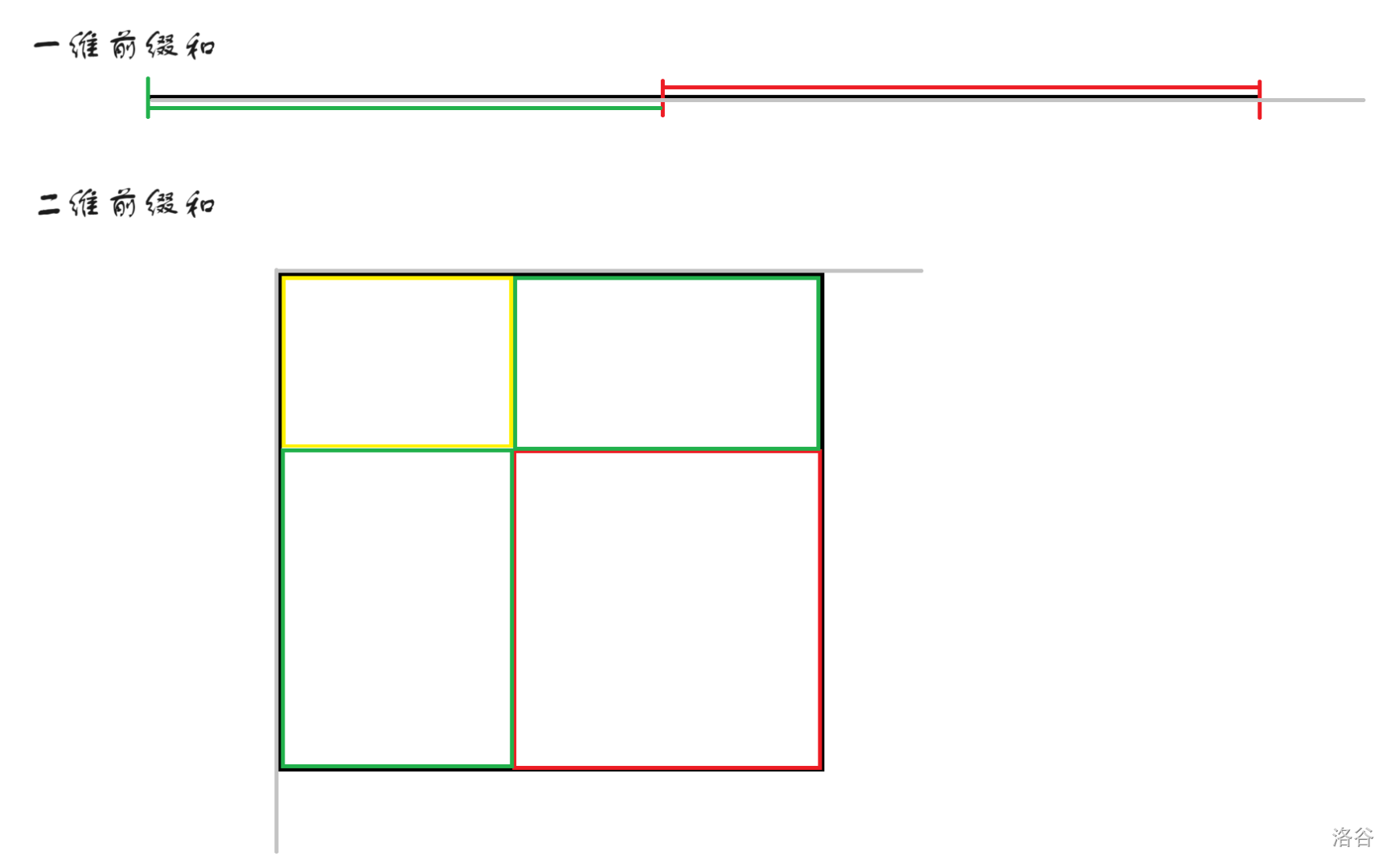
在一维序列中,红色部分的和就是黑色部分的和减掉绿色部分的和。那么前缀和的公式就是
在二维序列中,红色部分的和就是黑色部分的和减掉绿色部分的和,然后再加上黄色部分的和(因为黄色部分被减了 \(2\) 次)。
三维前缀和
三维前缀和同理,那么下面给出三维前缀和的图。
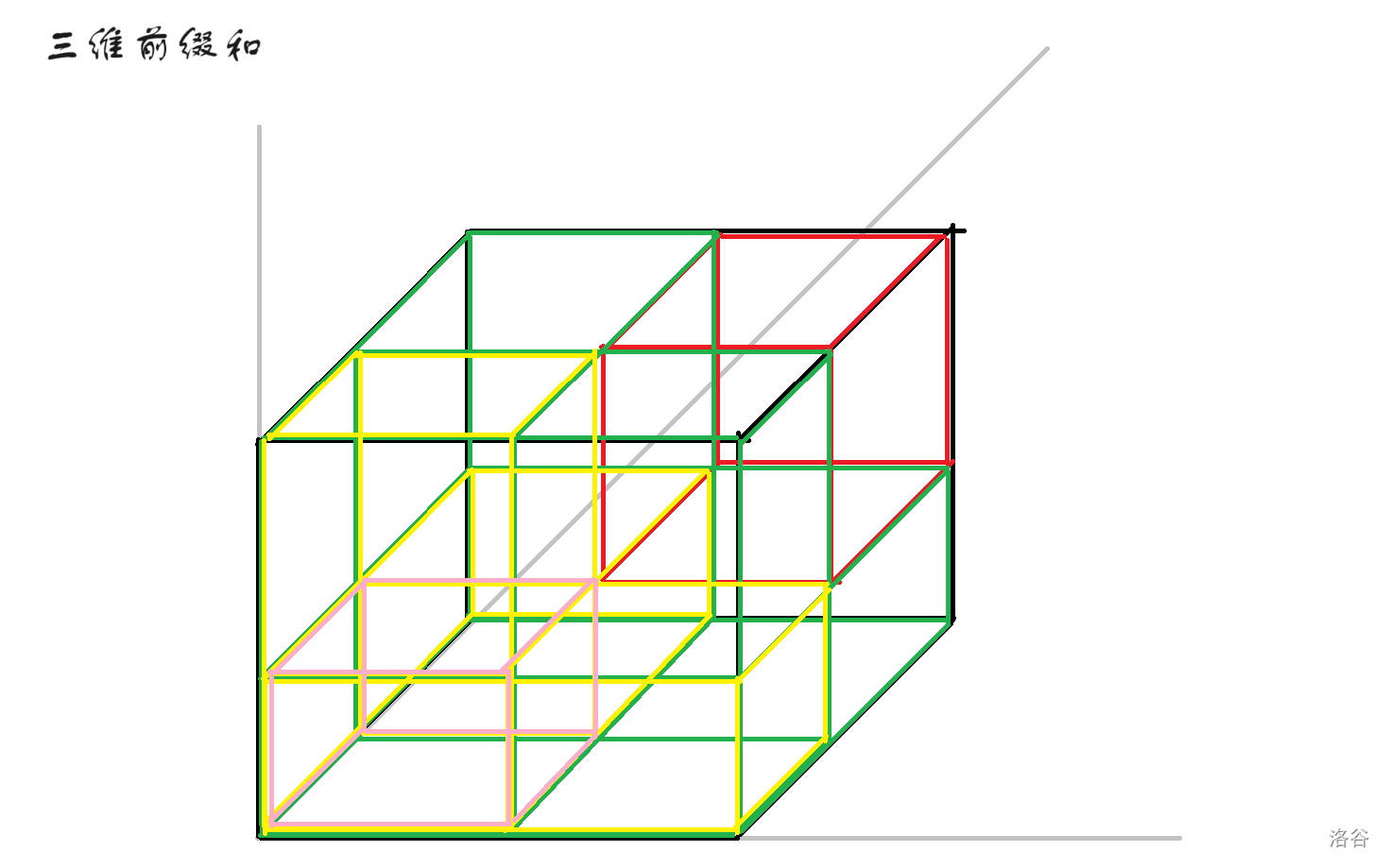
可以发现...这完全看不懂啊!
没关系,我们将它拆开研究。
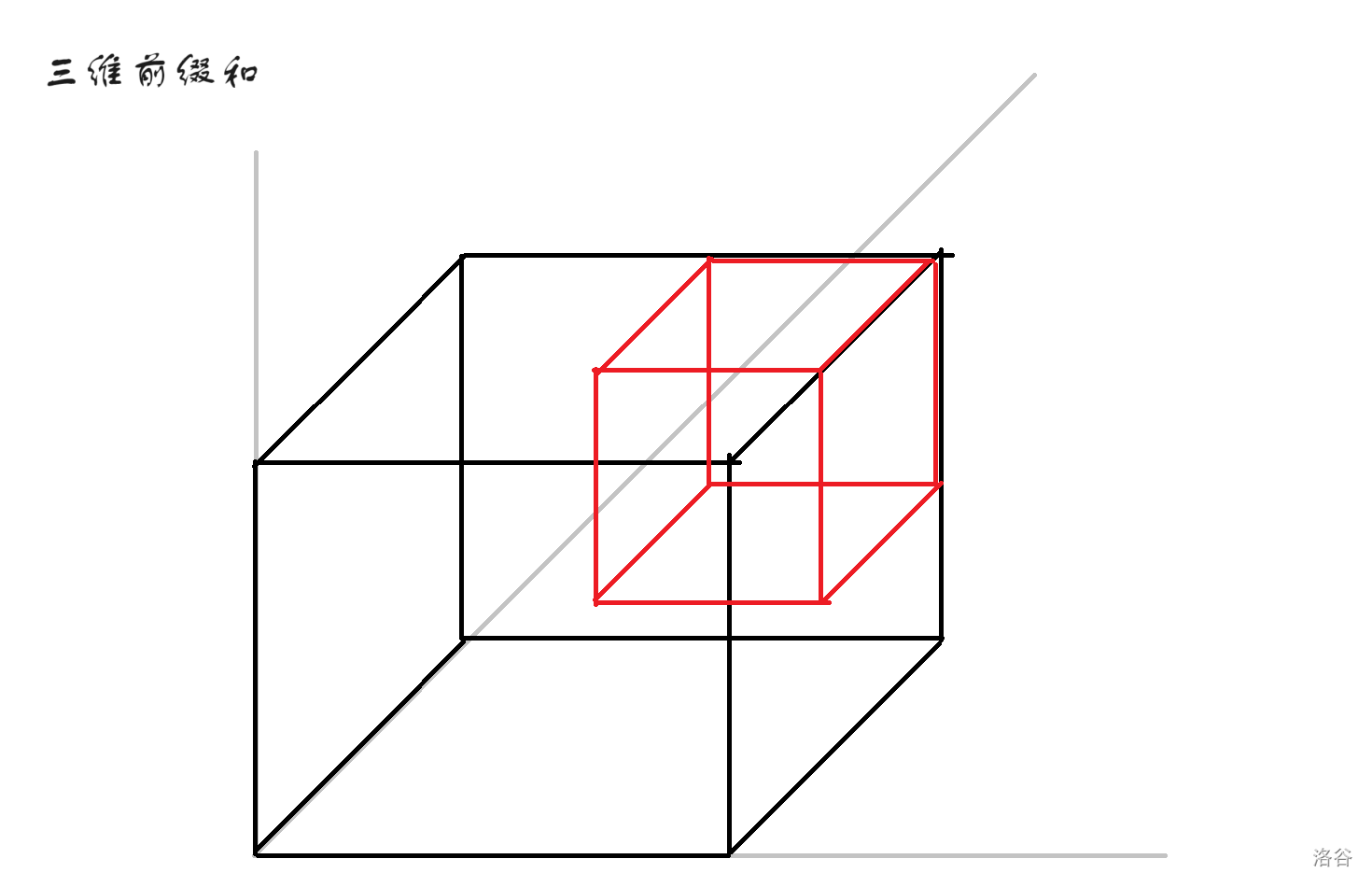
我们可以看到,黑色部分包括了要求的红色部分。那么我们就可以用黑色部分减掉剩余的部分,然后求出红色部分。
我们需要减掉这三个绿色部分:
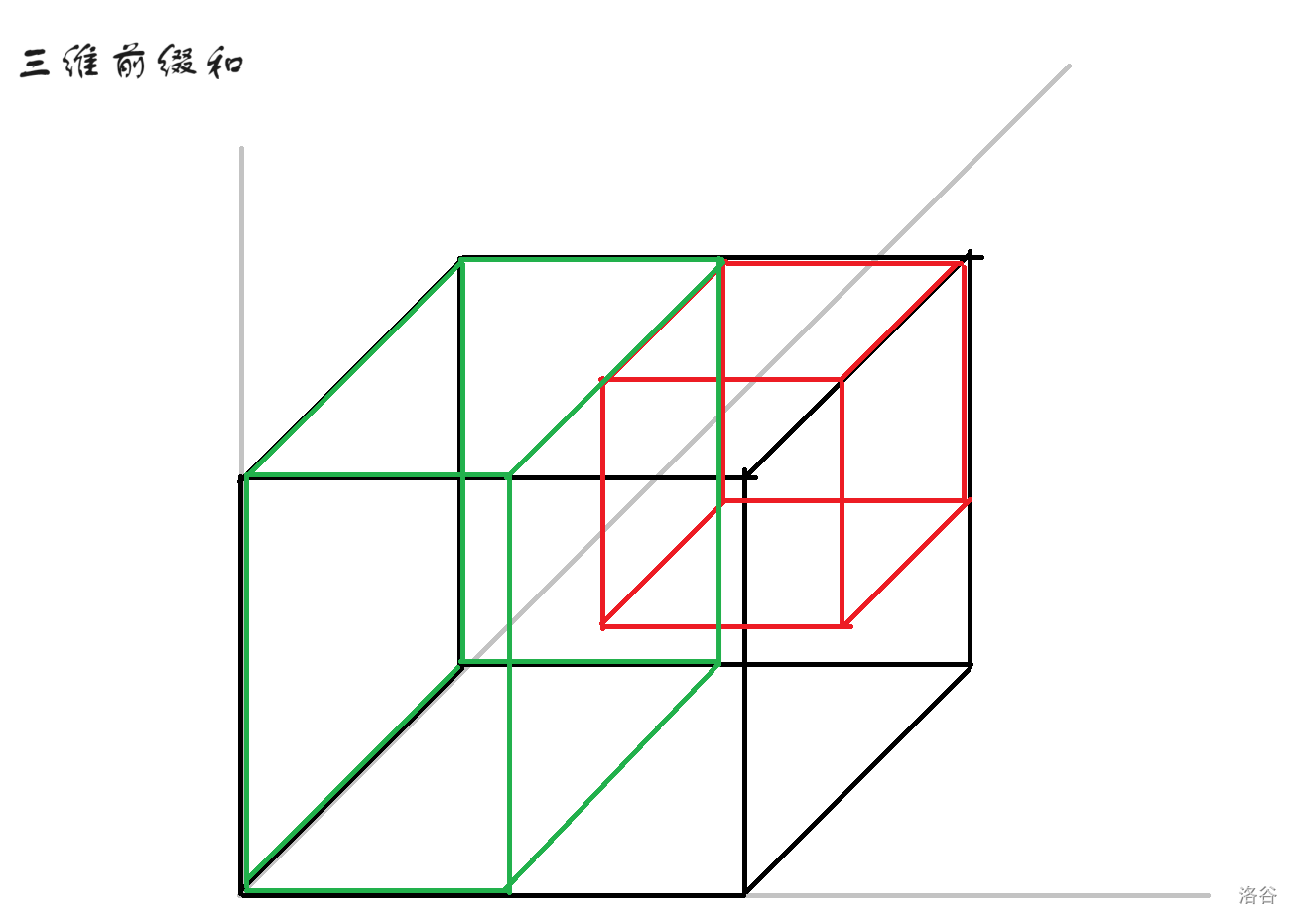
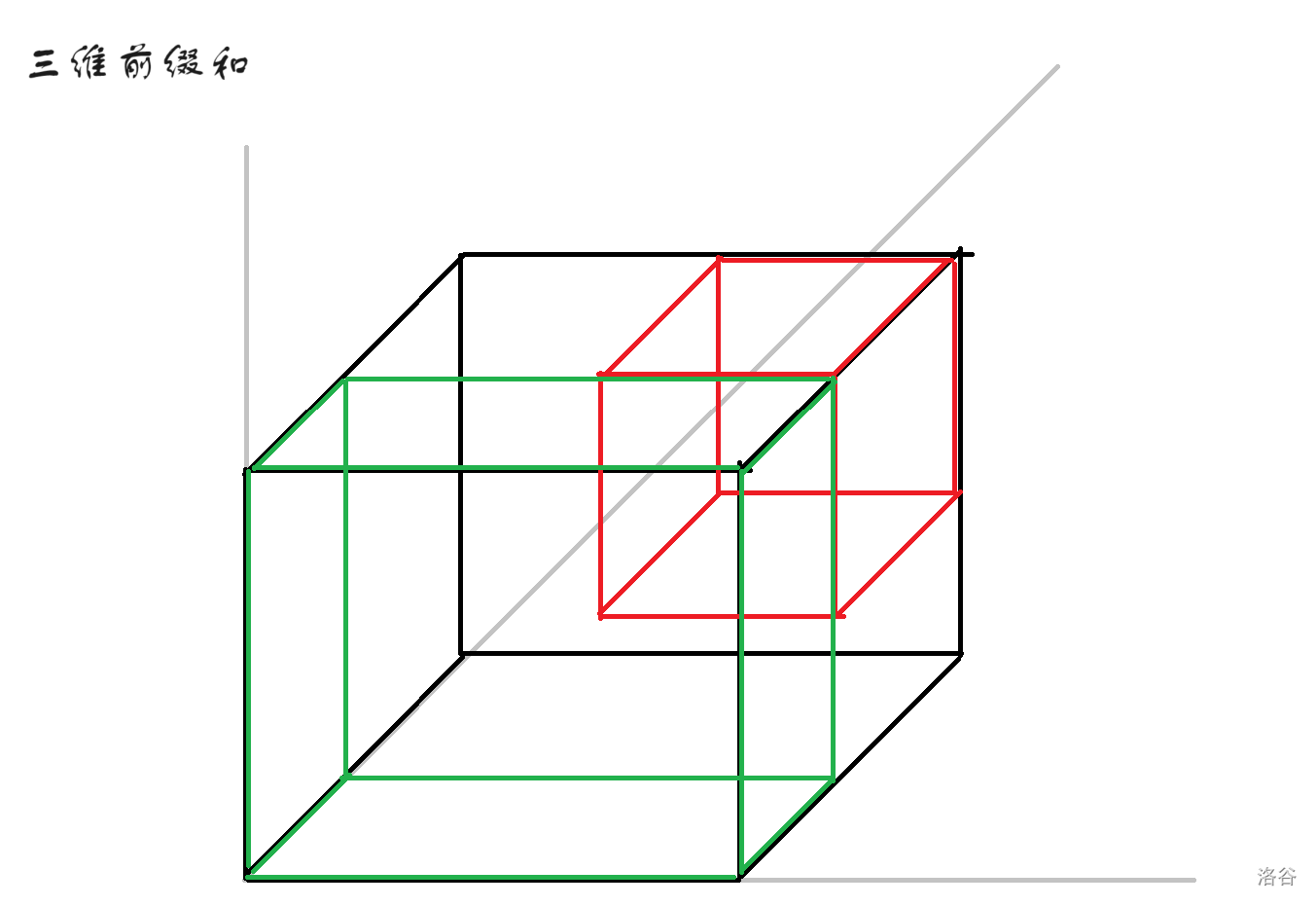
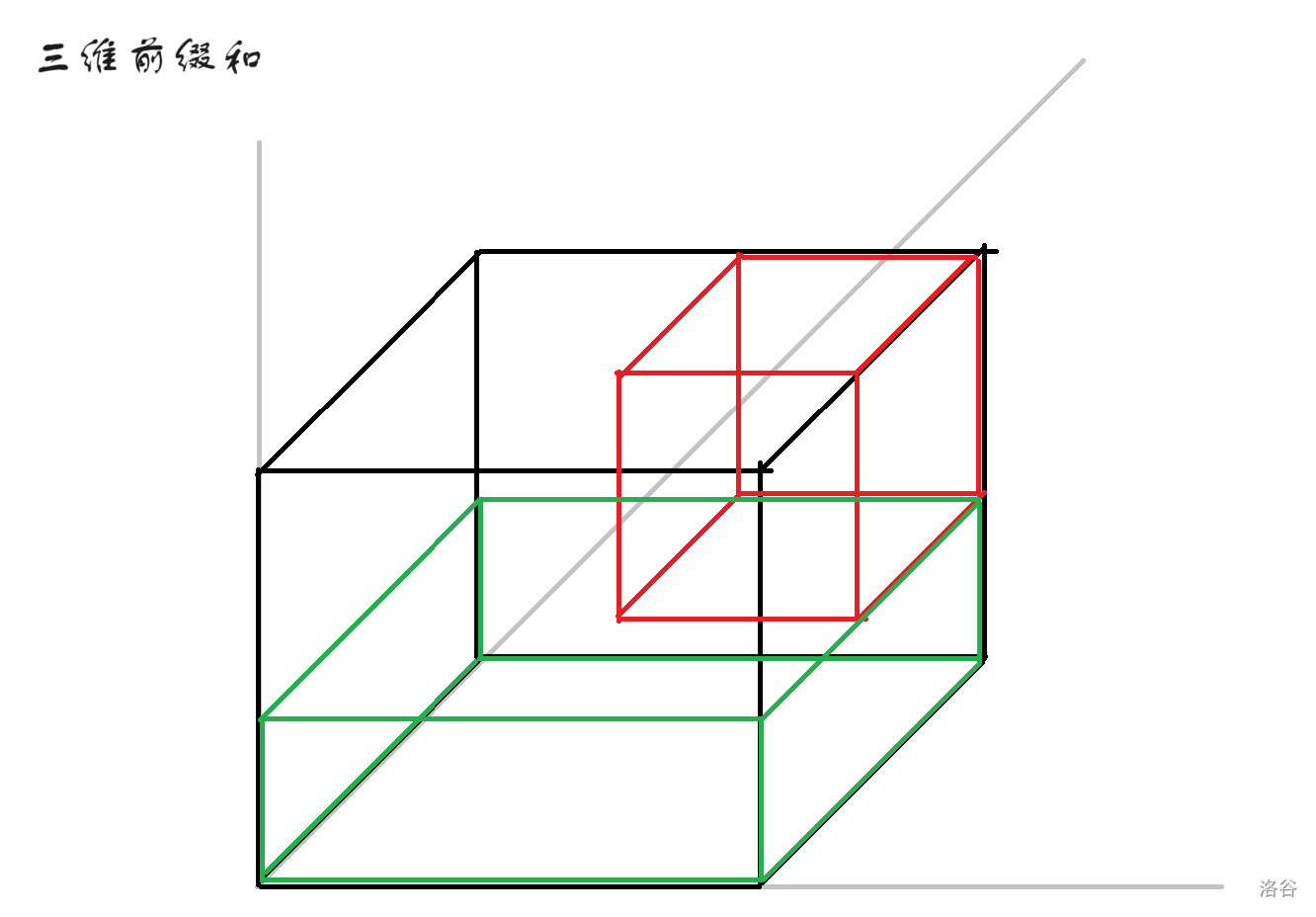
但是这时候又会发现一个问题,绿色部分的交(如图)被重复减了。
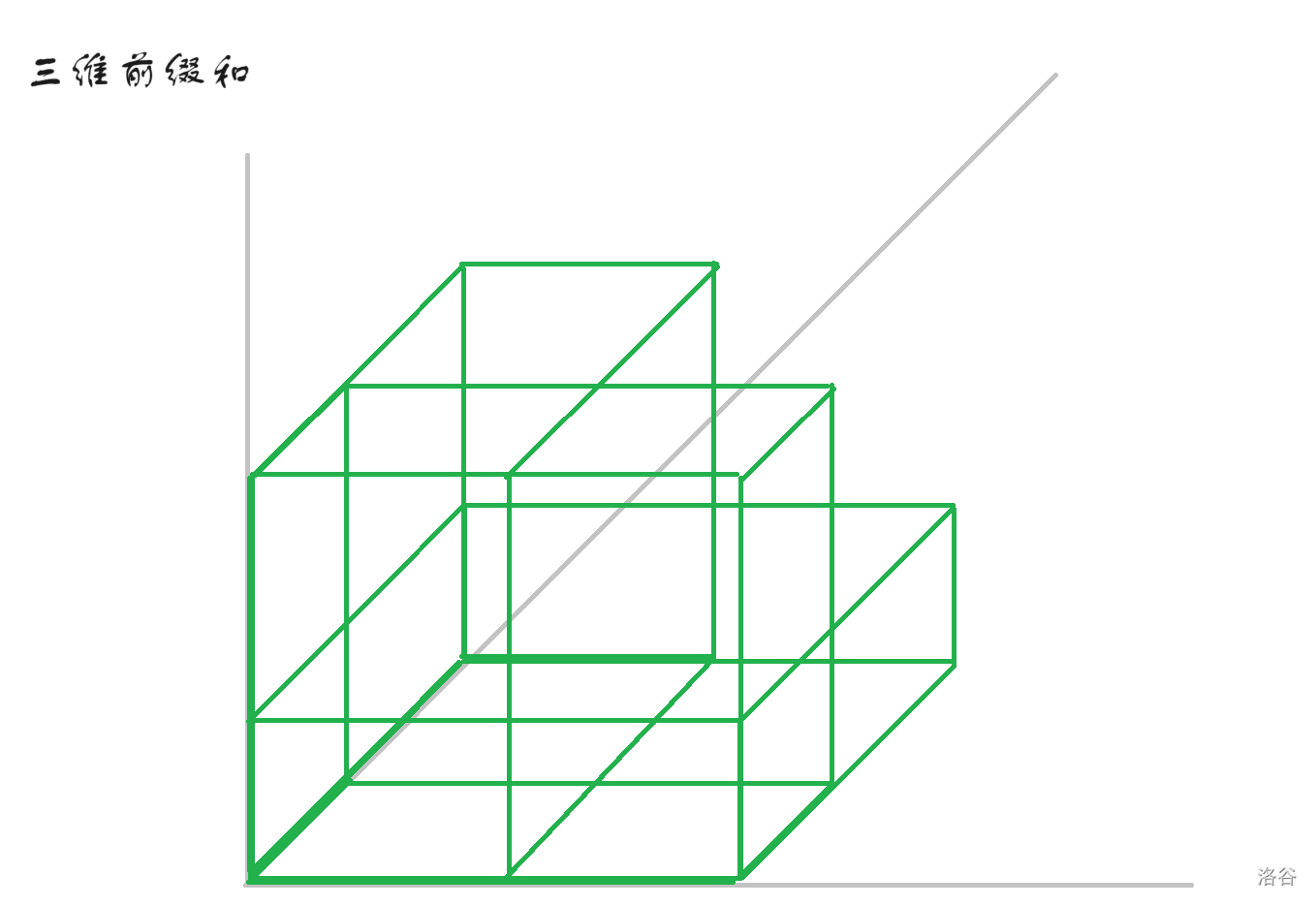
所以我们需要找到绿色部分两两的交,并且加回来。即下图的黄色部分。
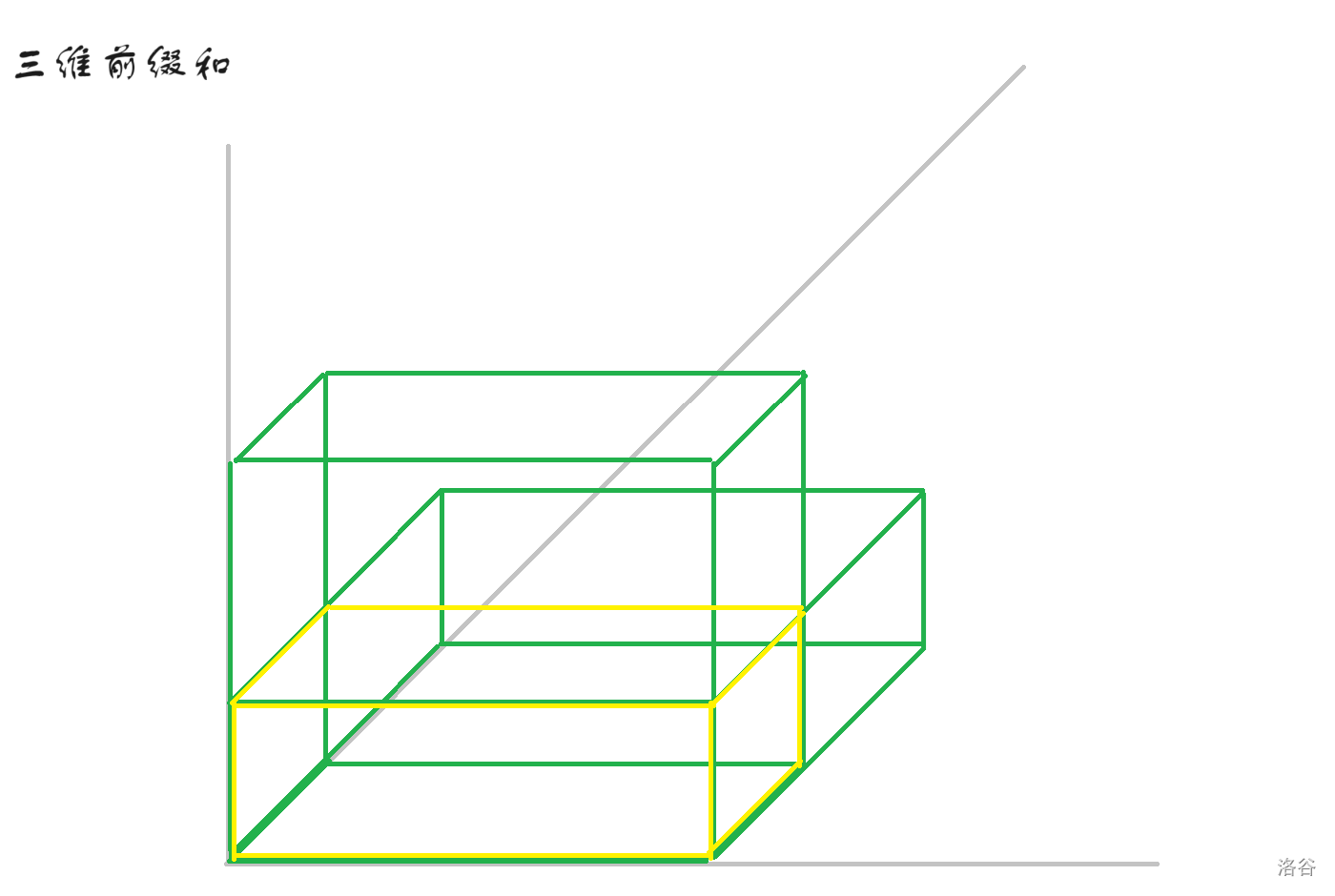
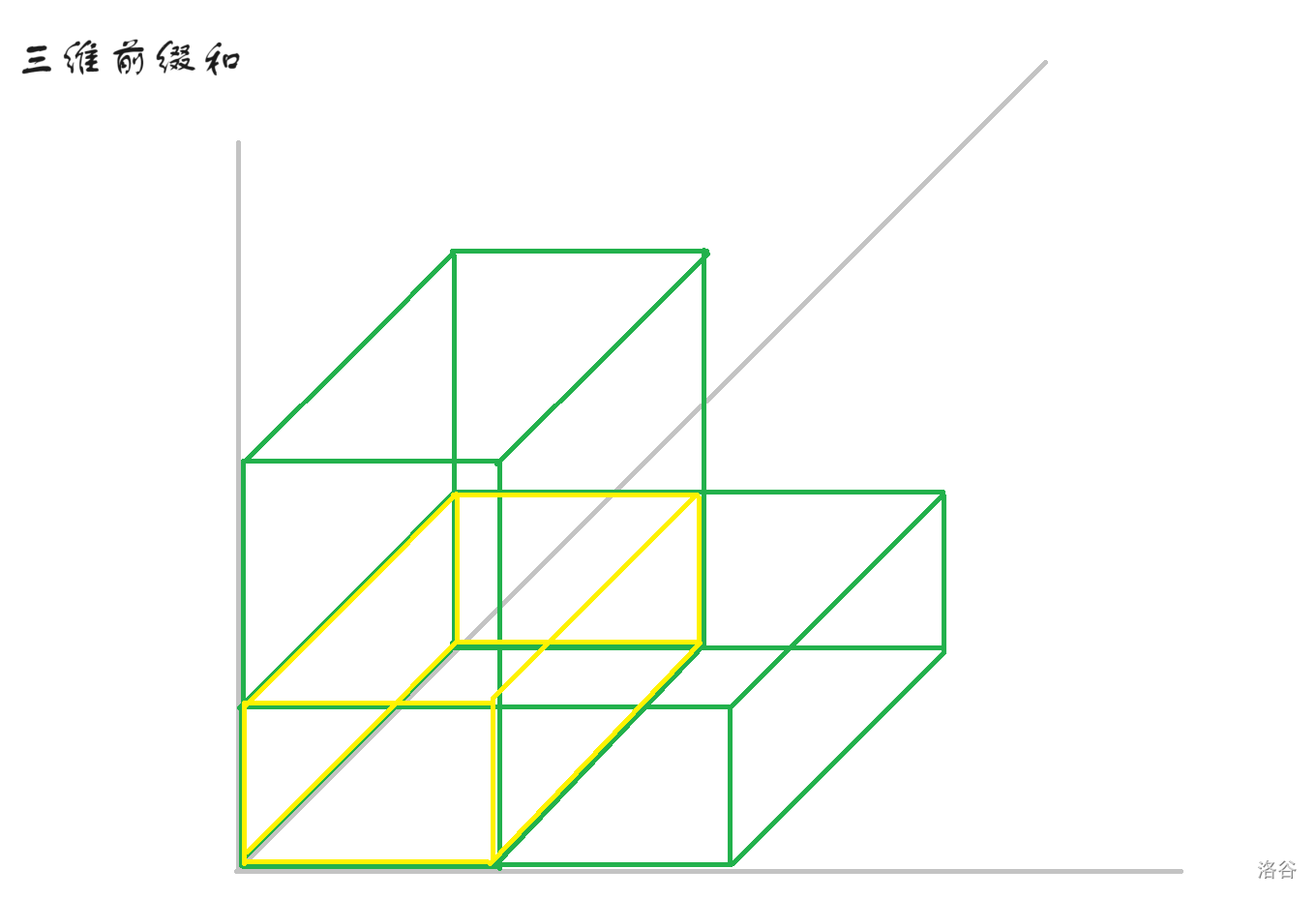
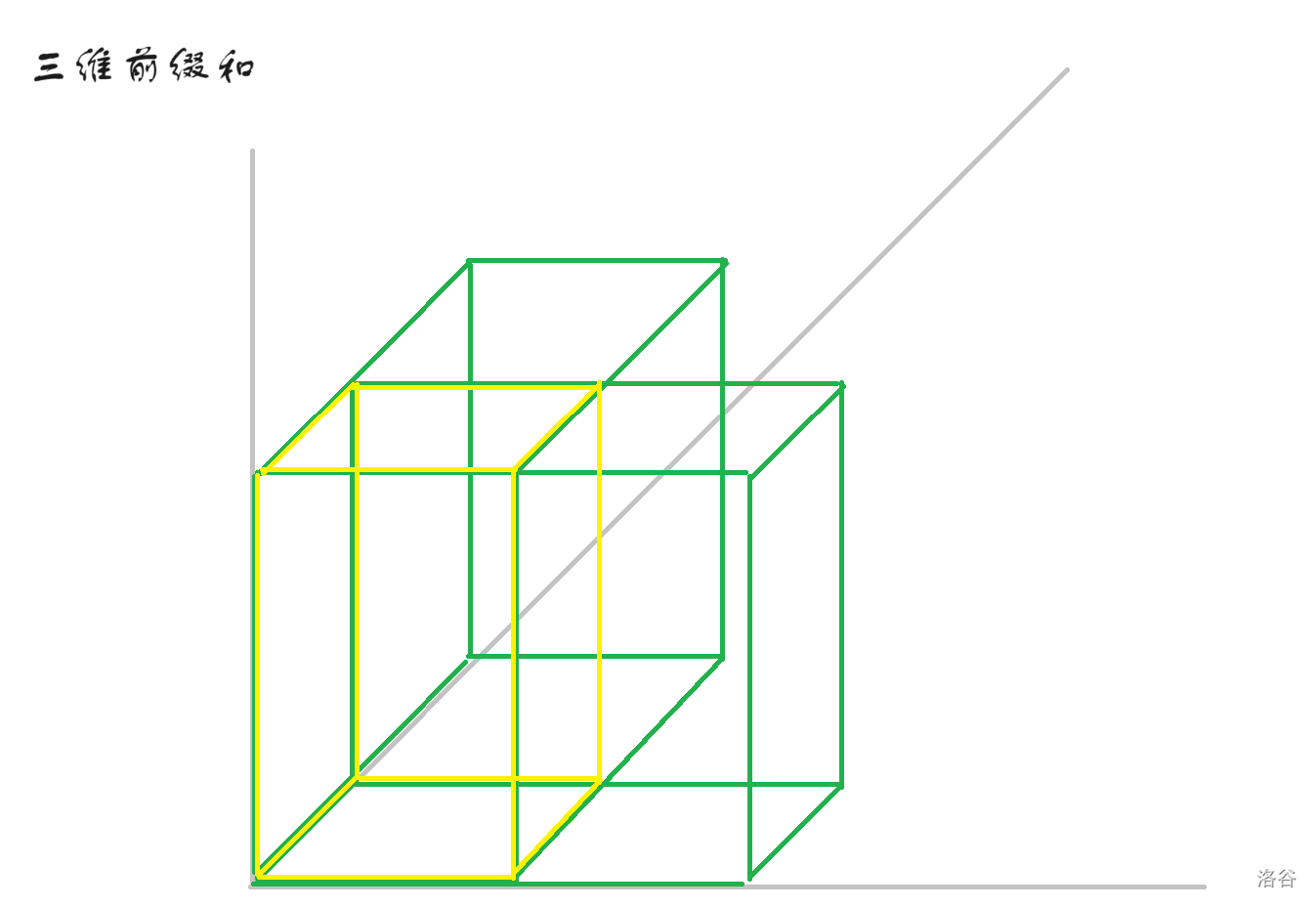
这时候,我们发现还是不对,黄色部分也有交!
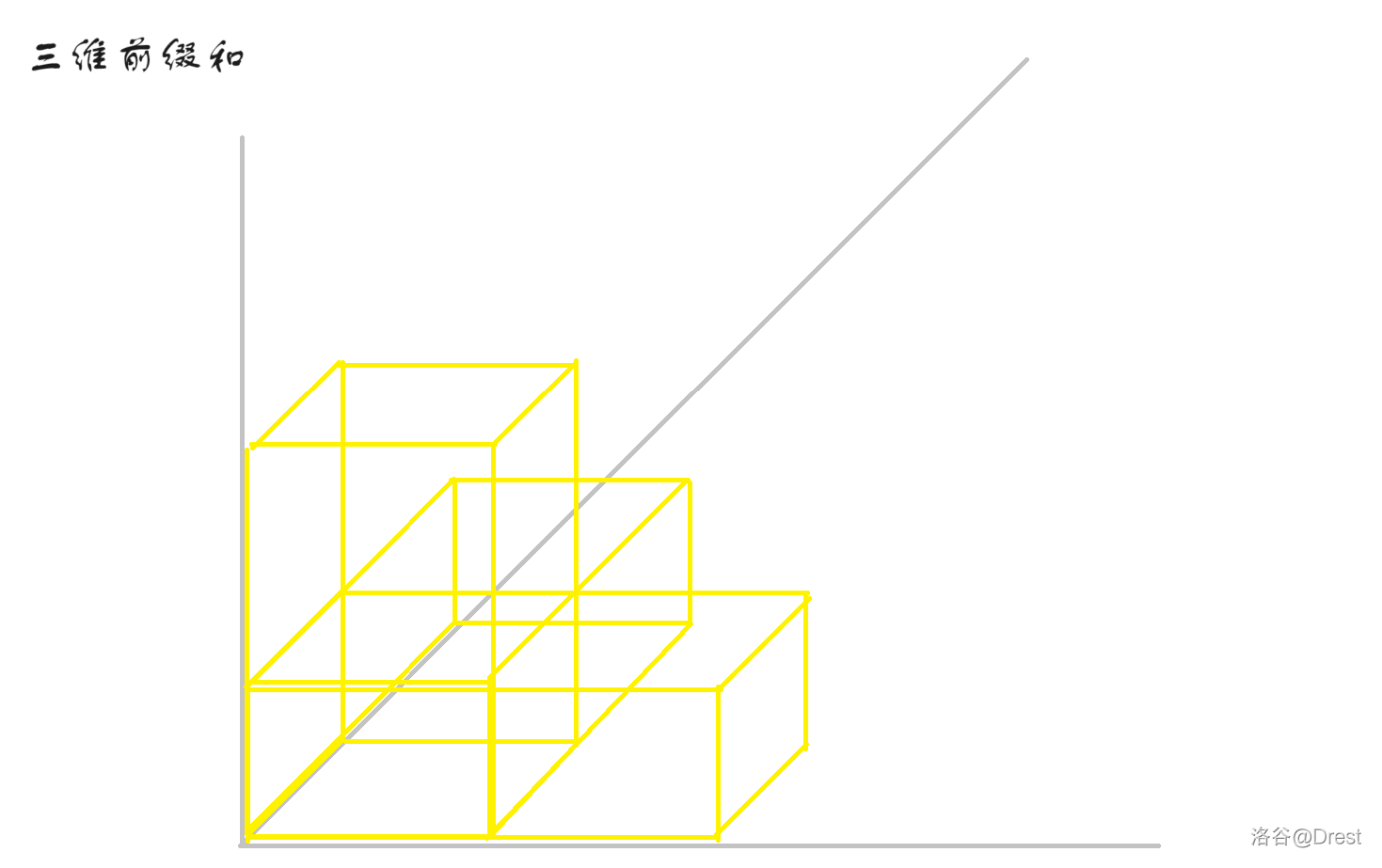
那么我们还需要将黄色部分的交(即下图粉色部分)再减掉。
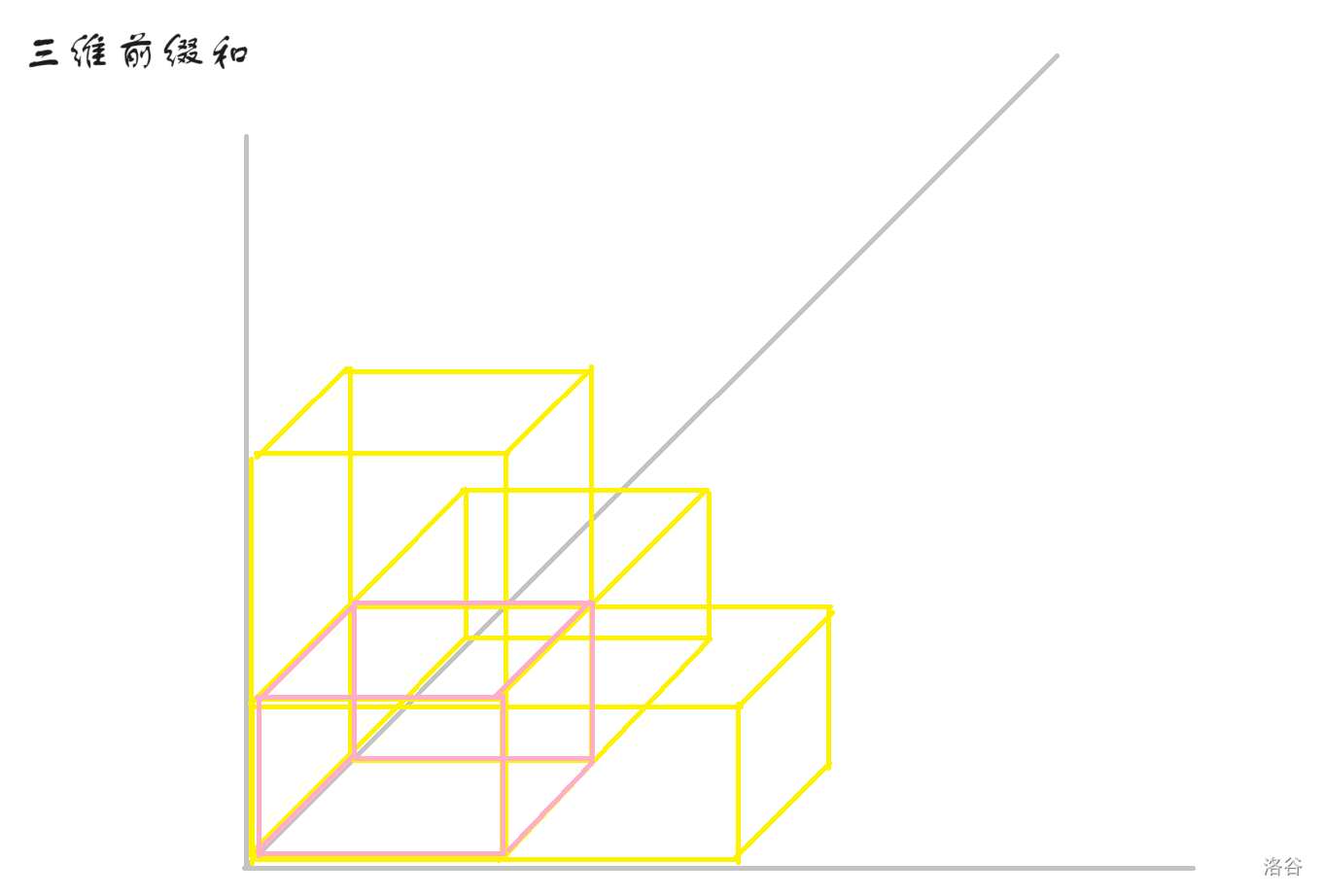
那么反过来,我们也可以推出前缀和的公式:
然后我们来看题。
可以发现这玩意就是一道三维前缀和的板子题,非常简单。
设 \(prefix[x][y][z]\) 为从 \((1,1,1)\) 到 \((x,y,z)\) 的区域的前缀和,我们需要查询从 \((Lx, Ly, Lz)\) 到 \((Rx, Ry, Rz)\) 的子立方体的和,公式为:
prefix[Rx][Ry][Rz] 是查询区域的总和的基础。
减去 \((Lx-1)\) 平面上的部分,表示区域中不包括 \(Lx\) 之前的部分。
减去 \((Ly-1)\) 平面上的部分,表示区域中不包括 \(Ly\) 之前的部分。
减去 \((Lz-1)\) 平面上的部分,表示区域中不包括 Lz 之前的部分。
加上 \((Lx-1, Ly-1)\) 立方体的部分,因为这个区域被多次减去了。
加上 \((Lx-1, Lz-1)\) 立方体的部分,因为这个区域被多次减去了。
加上 \((Ly-1, Lz-1)\) 立方体的部分,因为这个区域被多次减去了。
减去 \((Lx-1, Ly-1, Lz-1)\) 立方体的部分,因为这个区域被多次加回来了。
code
#include "bits/stdc++.h"using namespace std;const int MAXN = 100; int A[MAXN+1][MAXN+1][MAXN+1];int prefix[MAXN+1][MAXN+1][MAXN+1];int main() {int n, q;cin >> n ;// 读取三维数组数据for (int x = 1; x <= n; ++x) {for (int y = 1; y <= n; ++y) {for (int z = 1; z <= n; ++z) {cin >> A[x][y][z];}}}// 计算三维前缀和for (int x = 1; x <= n; ++x) {for (int y = 1; y <= n; ++y) {for (int z = 1; z <= n; ++z) {prefix[x][y][z] = A[x][y][z]+ (x > 1 ? prefix[x-1][y][z] : 0)+ (y > 1 ? prefix[x][y-1][z] : 0)+ (z > 1 ? prefix[x][y][z-1] : 0)- (x > 1 && y > 1 ? prefix[x-1][y-1][z] : 0)- (x > 1 && z > 1 ? prefix[x-1][y][z-1] : 0)- (y > 1 && z > 1 ? prefix[x][y-1][z-1] : 0)+ (x > 1 && y > 1 && z > 1 ? prefix[x-1][y-1][z-1] : 0);}}}cin >> q;while (q--) {int Lx, Rx, Ly, Ry, Lz, Rz;cin >> Lx >> Rx >> Ly >> Ry >> Lz >> Rz;// 前缀和查询范围内的和int result = prefix[Rx][Ry][Rz]- (Lx > 1 ? prefix[Lx-1][Ry][Rz] : 0)- (Ly > 1 ? prefix[Rx][Ly-1][Rz] : 0)- (Lz > 1 ? prefix[Rx][Ry][Lz-1] : 0)+ (Lx > 1 && Ly > 1 ? prefix[Lx-1][Ly-1][Rz] : 0)+ (Lx > 1 && Lz > 1 ? prefix[Lx-1][Ry][Lz-1] : 0)+ (Ly > 1 && Lz > 1 ? prefix[Rx][Ly-1][Lz-1] : 0)- (Lx > 1 && Ly > 1 && Lz > 1 ? prefix[Lx-1][Ly-1][Lz-1] : 0);cout << result << endl;}return 0;
}