时间复杂度简单计算(一层、两层、多层循环)
相当于轨迹追踪法:设执行次数为k,按照循环条件



阿布算法课
01 区别算法(Algorithm)和程序(Program)

| 算法 | 程序 |
|---|---|
| 设计阶段 | 实施阶段 |
| 相关领域知识 | 程序员 |
| 任何语言、伪代码 | 编程语言 |
| 独立于硬件/操作系统 | 与硬件/操作系统有关 |
| 算法分析 | 程序测试 |
02 事前分析和事后测试

| 事前分析 | 事后测试 |
|---|---|
| 算法 | 程序 |
| 独立于语言 | 有赖于语言 |
| 独立于硬件/操作系统 | 与硬件/操作系统有关 |
| 时间/空间 复杂度函数 | 运行时间/占用字节 |
03 算法的性质
-
一个或多个输入
-
至少有一个输出
-
可定义性
-
-
高效性
04 算法的表示和分析
怎么表示一个算法:需要看得懂,没有固定形式(伪代码)
如何分析一个算法?
-
Time:时间消耗
-
Space:内存消耗
-
N/W:数据传输和网络消耗
-
Power:能耗
-
CPU Registers:占用CPU多少寄存器(底层驱动、操作系统)
时间复杂度分析 
 时间复杂度函数 f(n) = 3
时间复杂度函数 f(n) = 3
-
算法时间复杂度分析,不需要考虑每个陈述语句形式。
-
算法时间复杂度看的是常数操作总次数
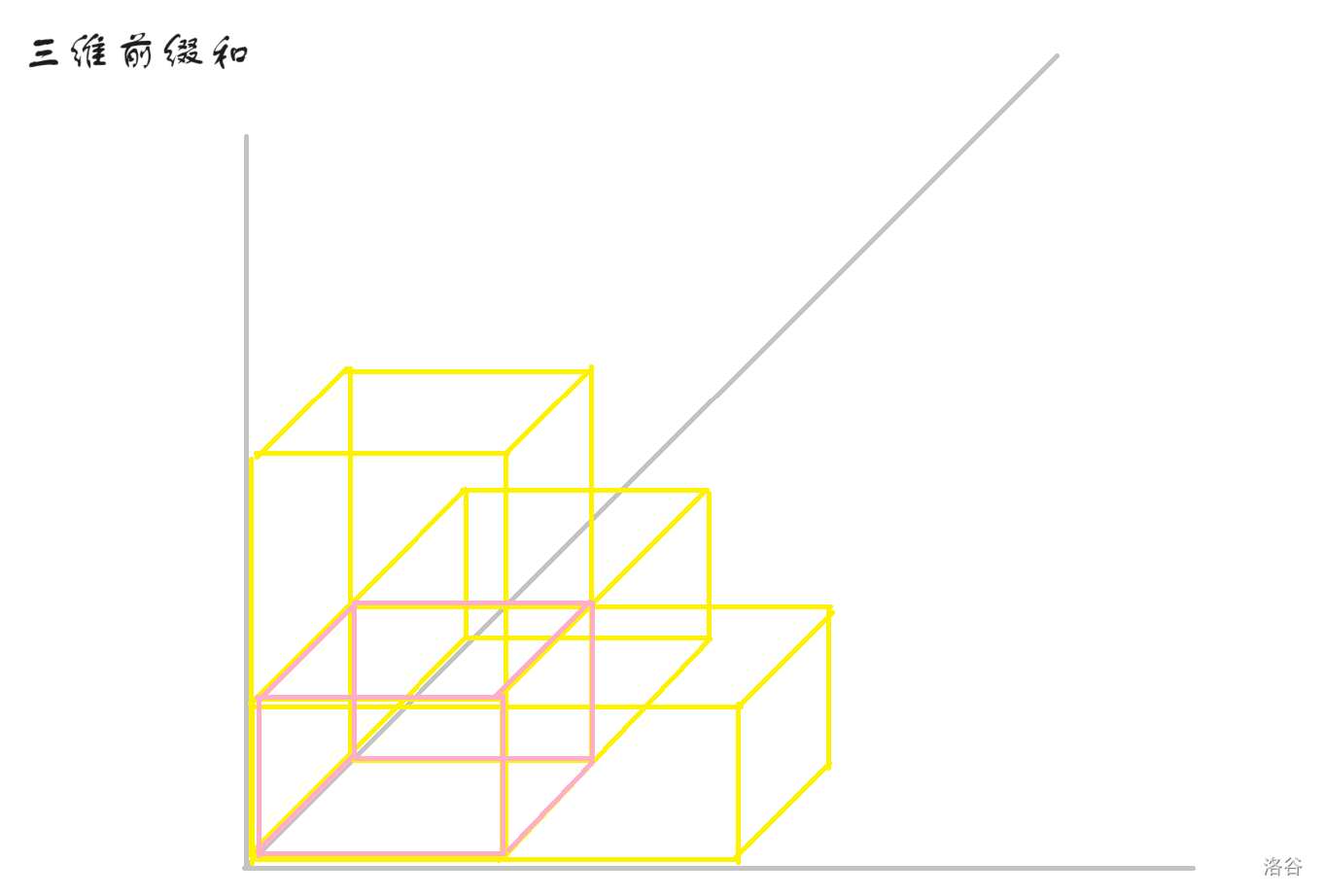
05 频数分析法求时间间复杂度
一层循环 
两层循环 
多层循环 
06 轨迹追踪法求时间复杂度
设执行次数为k,按照循环条件,得出执行次数k与问题规模n的关系,从而得时间复杂度 
07 时间复杂度分析示例
logn为小数,执行次数要向上取整
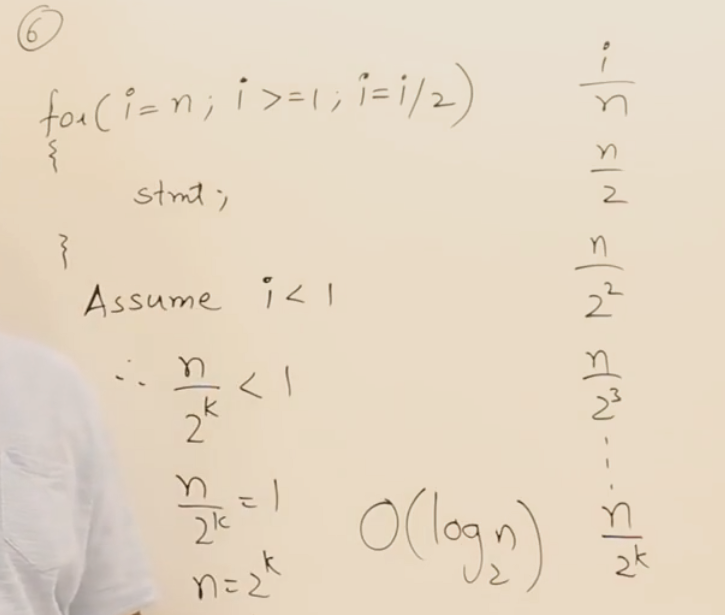
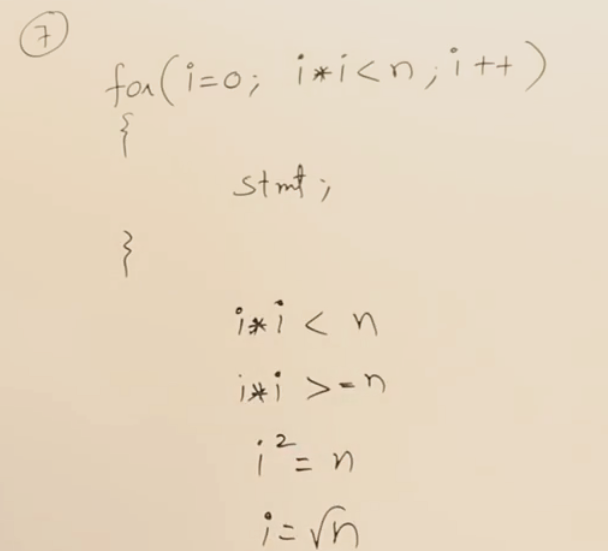
常见for循环时间复杂度总结:
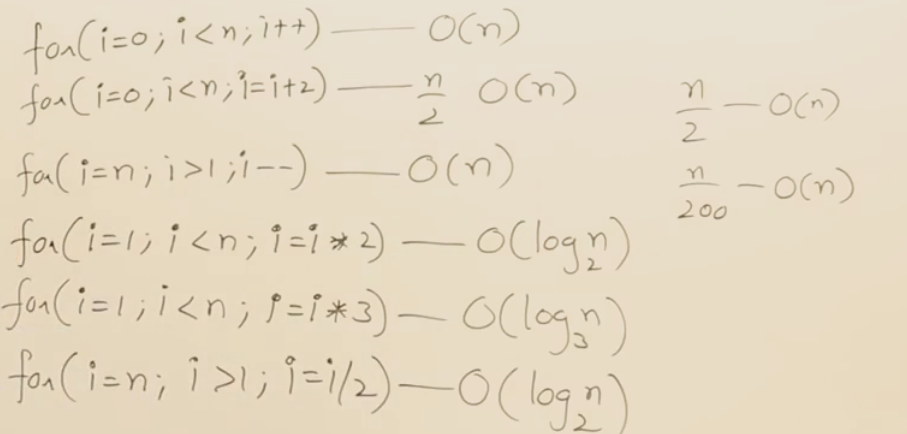
08 while循环、if条件的时间复杂度分析
由于while循环可以和for循环相互转换,while循环实际上和for循环分析方法一样
if 语句分析时间复杂度可能有最坏、最好情况
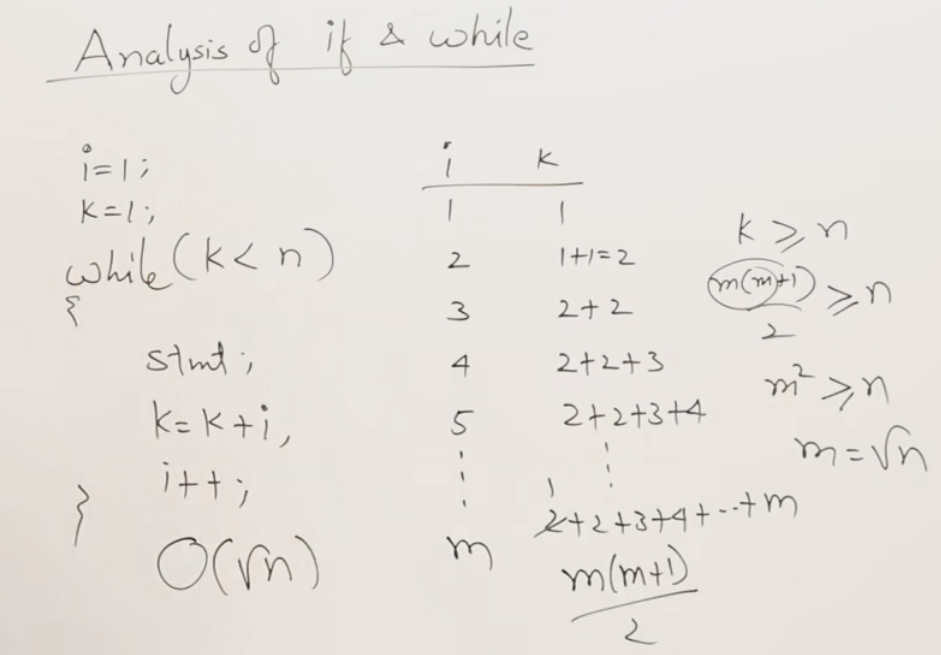
09 时间复杂度的分类
10 函数复杂度的比较和分析
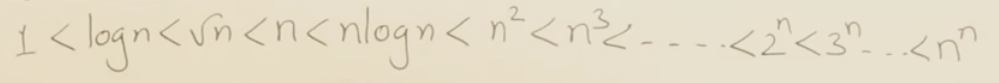
增长速度:常<对<幂<指数
11函数的渐近符号

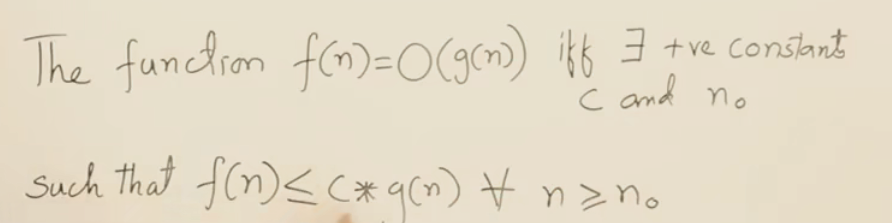
上界有很多,尽量使用最接近的那个上界表示f(n)
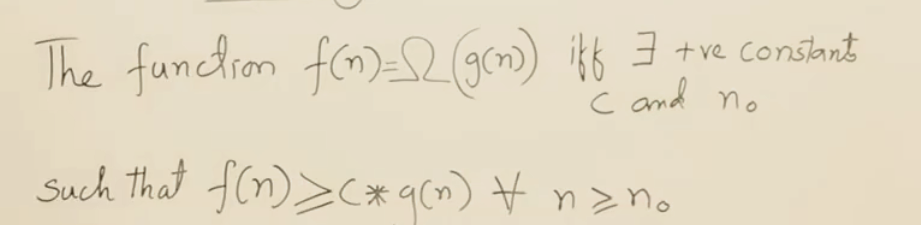
当下界有很多时,尽量使用最接近的那个下界表示f(n)
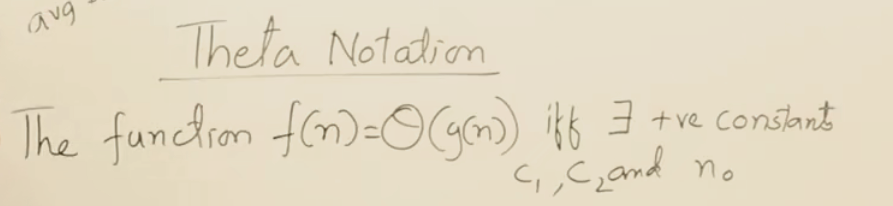
平均界只有一种表示方式表示f(n)
最好、最坏、平均情况的时间复杂度
-
算法的时间复杂度,会随着排序集合的有序性而改变。我们需要分析不同算法在不同数据下的表现
-
最好时间复杂度:在完全有序的情况下的时间复杂度
-
最坏时间复杂度:在最坏情况下的时间复杂度
-
平均复杂度:平均情况下的时间复杂度
-
注意:并不是最坏时间复杂度就用O(n),最好情况就是\Omega(n),平均情况就是\theta(n),O(),\Omega(),\theta()只是表示函数渐近的符号,都可以使用任何情况的时间复杂度衡量上。
最好、最坏、平均情况时间复杂度分析
线性搜索
二叉搜索树(二叉排序树)(二分搜索)
12深入学习函数渐近符号
阶乘形式的f(n)没有精确的平均界表示,只能通过上、下界表示
logn! = O(nlogn) = Ω(1)
13 渐近符号的性质
14 函数的比较
15 递归算法的时间复杂度
-
整个递归算法的时间复杂度函数用 T(n)表示
-
如何求得递归算法得时间复杂度函数T(n):
-
递归追踪树,求得T(n)表达式
-
由T(n)的递推关系,推导出T(n)
-
根据master公式得出T(n)的渐近表示
-
例1
例2
追踪递归树求T(n)
递归推导求T(n)
常见T(n)递归关系对应的时间复杂度

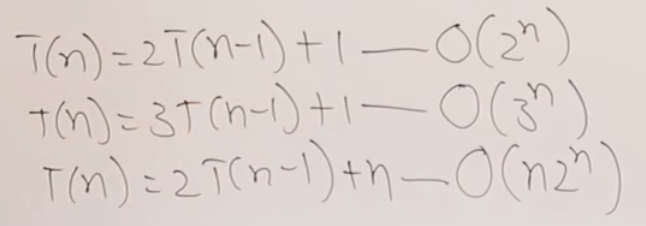
16 master公式
减法的master公式
Masters Theorem Decreasing Function

除法的master公式
Masters Theorem in Algorithms for Dividing Function 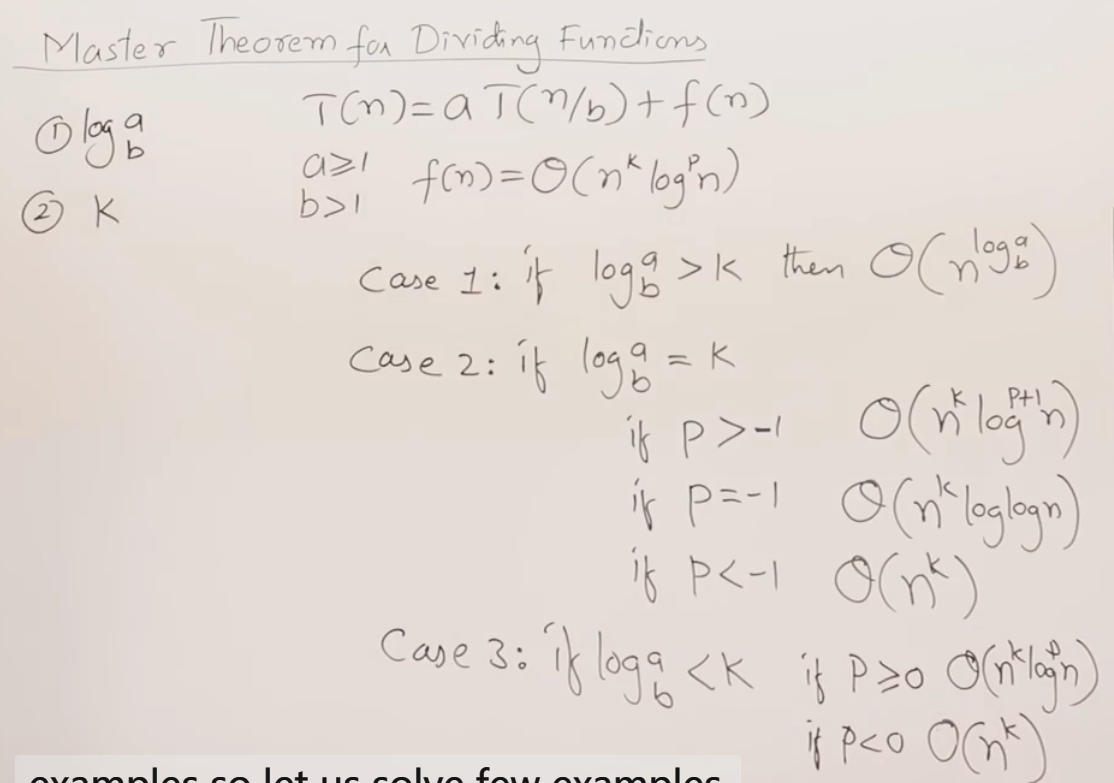
左神求递归复杂度:(以上的p=0的情况)
 N^d*logN 即 N^dlogN
N^d*logN 即 N^dlogN
其中:
-
T(N) 是问题规模为 N 时递归算法的时间复杂度
-
a(a>0)是子问题数量,子问题的规模相同,每一个子问题约耗时 T(N/b)
-
b 是问题规模缩减的程度,通常 b > 1
-
O(n^d) 是非递归部分的时间复杂度,通常较低阶

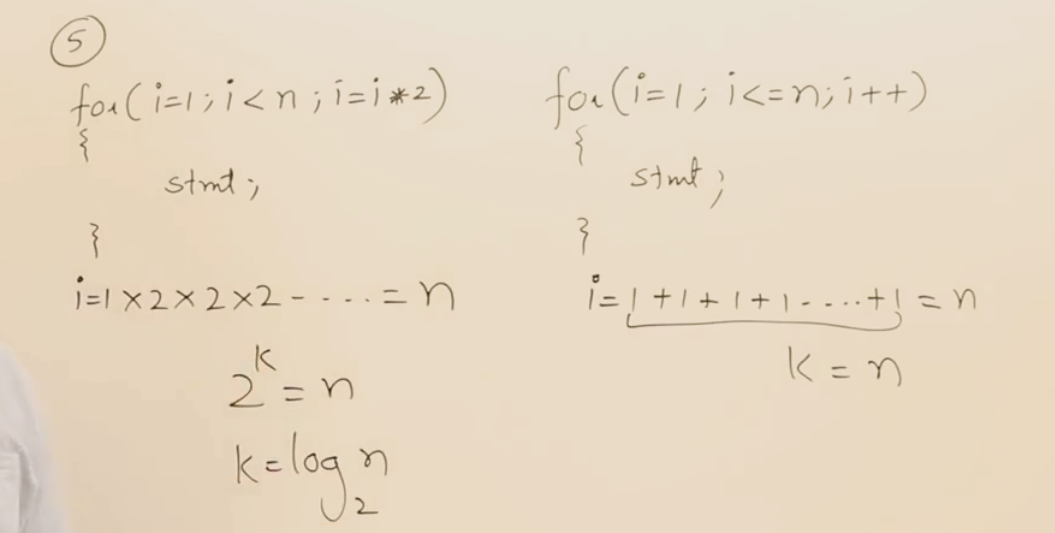

![【办公软件学习】如何交叉引用多个参考文献[x-x]](https://img2022.cnblogs.com/blog/2938556/202209/2938556-20220929105841190-391023978.png)
![[Java/SQL] 自动去除SQL注释](https://blog-static.cnblogs.com/files/johnnyzen/cnblogs-qq-group-qrcode.gif?t=1679679148)