Dynamic Range Compression Preserving Local Image Contrast for Digital Video Camera

Dynamic Range Compression Preserving Local Image Contrast for Digital Video Camera

数字摄像机中保持局部图像对比度的动态范围压缩

摘要

本文提出了一种新的数字摄像机动态范围压缩方法。该算法的目的是在像素和周围注意力区域的亮度比来保持局部对比度。通常，数字视频摄像机需要将阴影保持到中间范围亮度，这样的阴影区域往往包括主要对象，例如人脸区域。根据该要求，大多数数字视频摄像机已经采用拐点曲线作为动态范围压缩函数，仅压缩拐点以上的高亮区域。但是这种方法具有严重降低高亮区域对比度的缺点。为了克服这一弱点，该算法自动和自适应地增强高亮区域的局部图像对比度。结果显示，在不抑制阴影到中间亮度的情况下，逼真地再现了诸如蓝天的高亮区域。

关键词

数码摄像机、动态范围压缩、拐点函数、局部对比度

I.介绍

数字视频摄像机通常具有捕获具有约200%至600%亮度水平的高动态范围(high dynamic range, HDR)图像的能力，而大多数显示设备具有仅具有约110%亮度水平的低动态范围(low dynamic range, LDR)。因此，动态范围压缩技术对于显示由数字视频摄像机捕获的图像是必不可少的。在许多情况下，通过动态范围压缩来保持阴影到中间亮度范围中的输入水平，从而不降低诸如面部区域的主被摄体的亮度。因此，大多数传统的数字摄像机采用拐点曲线作为动态范围压缩函数。如图1所示，该方法强烈地压缩了拐点上的高光范围，因此高光区域(例如天空区域)中的对比度大大降低。在此基础上的改进算法会使用自动拐点函数曲线。该方法旨在通过根据最大亮度水平或高光区域中的像素数量调整拐点，自适应地为高光范围分配更多的色调级别。然而，自动膝关节略微提高了高光对比度，而不是降低中间范围内的亮度。

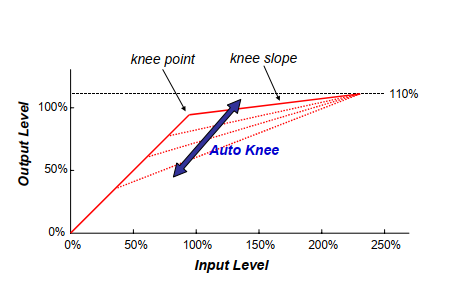
图1 传统拐点曲线和自动拐点曲线

这些技术是空间不变的算法，与传统的高动态范围压缩算法[1-4]一样，它们将单个色调映射曲线均匀地应用于整个图像。这些方法的优点在于它们的简单性和计算效率，通过使用查找表的一对一映射。然而，使用单调增加的色调映射曲线很难同时保持阴影和高光区域的视觉对比度。

另一方面，最近提出了一些空间变化色调映射算法[5,6]。由于它们将不同的变换应用于图像的不同部分，因此它们实现了灵活的色调映射。一些以前的工作，如Fattal等人[7]表明，重要的是色调再现保持局部图像对比度，这意味着像素与其局部周围的亮度比。此外，Jobson等人[8]提出了一种基于Land的“retinex”理论[9]的动态范围压缩方法，该理论是亮度和颜色感知的视觉模型。他们的中心/环绕模型通过取像素亮度与其低通滤波的对数比来去除空间变化的光源。Chiu等人也提出了类似的算子[10]。然而，之前的大多数空间变化色调映射算法都没有阐明色调映射水平与局部图像对比度之间的关系。因此，很难将这些方法应用于数字视频摄像机的动态范围压缩，因为基本色调映射曲线应易于控制，以保持阴影到中等的亮度映射，同时保持在任何亮度水平下，视觉对比度尽可能与原始相同。此外，以前的工作需要很多参数，充分设置参数也是相当困难的[11]。

为了解决这些问题，本文提出了一种新的数字视频摄像机动态范围压缩算法[12]。

我们假设，如果在任何像素的局部对比度不改变，视觉对比度也被保留。基于这一假设，我们首先开发了一种新的算子来保持局部对比度。该算子根据给定的基本色调映射曲线，自动增强局部对比度，并在任何亮度水平下保持其接近原始图像。第二节介绍了这一算子。

接下来，我们尝试将此算子应用于数字摄像机的动态范围压缩。特别地，为了保持高光对比度而不降低阴影到中间范围亮度的质量，应当适当地确定基本色调映射曲线。第三部分介绍了数码摄像机基本色调映射曲线的功能设计方法。

应用所提出的算法，捕获的图像在任何亮度水平都可以再现逼真的高对比度。在第四节中，实验证明了所提出的算法的性能。

最后，第五节介绍了结论和讨论情况。

II.NOVEL OPERATOR FOR PRESERVING LOCAL IMAGEC ONTRA

视觉对比度高度依赖于局部对比度，局部对比度是指像素与其局部周围的亮度比。但空间不变的色调映射曲线无法保持局部图像对比度。另一方面，我们提出了一种新的算子以保持局部对比度。我们称之为局部对比度范围变换LCRT(Local Contrast Range Transform)。
LCRT的概念如图2所示。

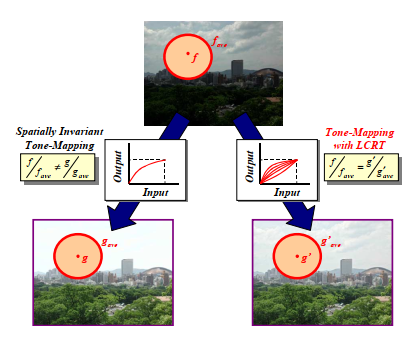
图2 LCRT概念图

保持局部对比度的数学条件描述如下。

\[\frac{g(x,y)}{g_{ave}(x,y)}=\frac{f(x,y)}{f_{ave}(x,y)} \tag{1} \]

这里，\(f(x,y),f_{ave}(x,y)\)表示输入图像\((x,y)\)处的亮度和局部平均亮度，\(g(x,y),g_{ave}(x,y)\)分别表示每个像素(x,y)的输出亮度水平和输出局部平均亮度。通过对\((1)\)的两边取对数，等式重写如下，

\[G(x,y)-G_{ave}(x,y)=F(x,y)-F_{ave}(x,y) \tag{2} \]

其中，\(F(x,y),F_{ave}(x,y),G(x,y),G_{ave}(x,y)\)分别表示\(f(x,y),f_{ave}(x,y),g(x,y),g_{ave}(x,y)\)的对数值。等式(2)表示在对数域中保持像素值与其局部平均值之间的差的数学条件。根据该条件，保持局部对比度的色调映射函数应满足以下等式。

\[G(x,y) = P\big(F(x,y)\big) + \Bigg\{1- \frac{dP\big(F(x,y)\big)}{dF(x,y)} \Bigg\} \cdot \big( F(x,y)-F_{ave}(x,y)\big) \tag{3} \]

其中\(P\big(F(x,y)\big)\)表示双对数域中的任意色调映射曲线。该方程通过一阶泰勒展开近似如下，

\[P\big(F_{ave}(x,y)\big) \cong P\big(F(x,y)\big) + \Bigg\{ \frac{dP\big(F(x,y)\big)}{dF(x,y)} \Bigg\} \cdot \big( F_{ave}(x,y)-F(x,y)\big) \tag{4} \]

此外，假设近似满足以下等式。

\[G_{ave}(x,y) \cong P\big(F(x,y)\big) \tag{5} \]

用\((4)\)和\((5)\)代替\((2)\)，则导出\((3)\)。
这里，将\(P\big(F(x,y)\big)\)转换到亮度域可表示为\(p\big(f(x,y)\big)\)，\((3)\)被重写为作为LCRT的基本公式的以下等式(参见附录)。

\[g(x,y)=p\big(f(x,y) \big) \times q\big(f(x,y), f_{ave}(x,y) \big) \tag{6} \]

在该等式中，右侧的第一分量\(P\big(F(x,y)\big)\)根据其输入亮度水平给出每个像素的基本色调映射水平。另一方面，第二分量\(q\big(f(x,y),f_{ave}(x,y)\big)\)给出局部对比度增强，并且可以描述如下。

\[q\big(f(x,y), f_{ave}(x,y) \big) = \Bigg( \frac{f(x,y)}{f_{ave}(x,y)}\Bigg)^{1-\frac{f(x,y)}{p(f(x,y))}\cdot \frac{dp(f(x,y))}{df(x,y)} } \tag{7} \]

当输入亮度水平\(f(x,y)\)等于其局部平均值\(f_{ave}(x,y)\)时，\((6)\)中的输出亮度水平\(g(x,y)\)正好映射到基本色调映射曲线\(p\big(f(x,y)\big)\)上。该基本色调映射曲线\(p\big(f(x,y)\big)\)可以针对不同目的任意确定，因此该算法非常灵活。一旦给出了基本色调映射曲线，第二分量\(q(f(x,y),f_{ave}(x,y))\)自动增强每个亮度级处的局部对比度，以将其保持为与原始的对比度一样。更具体地，输入亮度\(f(x,y)\)与局部平均值\(f_{ave}(x,y)\)的比率在处理前后保持一致。
此外，我们修改\((3)\)如下。

\[G(x,y)=P\big(F(x,y)\big)+\alpha \cdot \Bigg\{1-\frac{dP\big(F(x,y)\big)}{dF(x,y)} \Bigg\} \cdot \big( F(x,y)-F_{ave}(x,y) \big) \tag{8} \]

在亮度域中，该等式也被重写为以下等式。

\[g(x,y)=p\big(f(x,y) \big)\times r\big(f(x,y),f_{ave}(x,y) \big) \tag{9} \]

\[r\big(f(x,y),f_{ave}(x,y) \big) = \Bigg(\frac{f(x,y)}{f_{ave}(x,y)} \Bigg)^{\alpha \cdot \Big\{1-\frac{f(x,y)}{p(f(x,y))} \cdot \frac{dp(f(x,y) )}{df(x,y)} \Big\} } \tag{10} \]

在这些等式中，$\alpha \(表示用于局部对比度增强的增益参数。当\)\alpha $被设置为\(1.0\)时，等式\((9)\)和\((10)\)分别等同于等式\((6)\)和\((7)\)，并且变换图像的局部对比度被保持为与原始图像的局部对比度一样多。另一方面，对于$\alpha<1.0 $ ，局部对比度增强较弱，$\alpha>1.0 \(时较强。根据应用的每个目的，该参数\)\alpha \(可以被确定为输入亮度水平\)f(x,y)\(和局部平均值\)f_{ave}(x,y)$的函数。

\((9)\)和\((10)\)中的局部平均\(f(x,y)\)通过如下进行空间平均滤波器\(A(x,y)\)和输入图像\(f(x,y)\)的卷积来计算，

\[f_{ave}(x,y) = \langle A(x,y)\otimes f(x,y) \rangle \tag{11} \]

在我们的基本模型中，以高斯滤波器作为空间平均滤波器，公式如下。

\[A(x,y) = K \exp\{-(x^2+y^2)/\sigma^2 \} \tag{12} \]

在该等式中，\(K\)是用于归一化滤波器系数的增益因子，

\[\iint A(x,y) dxdy =1 \tag{13} \]

此外，$\sigma \(表示确定核大小\)M\(的标准差。实际上，考虑到\)±2\sigma \(的扩展，对于\)\sigma \(的整数值，核大小\)M=4\sigma +1$应该是足够的。

III.LCRT在数字视频中的应用

数码摄像机要求满足的条件是动态范围压缩，阴影到中间亮度范围、包括主对象不会降低。为此会采用拐点曲线作为动态范围压缩函数，但是难以同时保持高亮区域的对比度。针对这一问题，本文提出了一种基于LCRT的动态范围压缩算法。本节详细介绍了确定数字摄像机和整个系统的基本色调映射曲线的实用方法。

A.数码摄像机的基本色调映射曲线

通常，将传统的拐点曲线应用于由相机伽马处理的图像。因此，在本节中，我们将处理亮度由相机伽马处理的域中的色调再现，我们称之为相机伽马域。

如前一章所述，一旦确定了\((9)\)中的任何基本色调映射曲线，我们就可以将LCRT应用于色调映射曲线，并在保持局部图像对比度的情况下实现动态范围压缩功能。为了保持阴影到中间亮度范围，优选地选择传统的拐点曲线作为基本色调映射曲线。然而，传统的拐点曲线在拐点处的一阶微分系数具有不连续性。如\((10)\)所示，为了保持由LCRT处理的结果图像的连续性，基本色调映射曲线中的信号电平和一阶微分系数必须是连续的。

为了满足这个条件，我们提出了近似使用三次曲线的拐点曲线如下(见图3)。

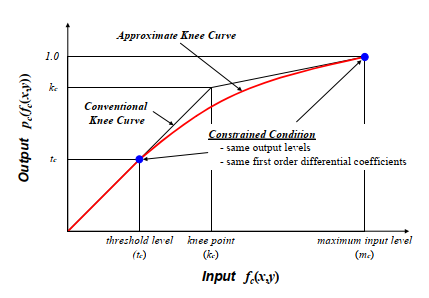
图3 近似拐点曲线

\[\begin{aligned} &if(f_c(x,y)<t_c) \\ &\qquad p_c\big(f_c(x,y) \big)=f_c(x,y) \\ &else \\ &\qquad p_c\big( f_c(x,y) \big)=a\cdot f_c(x,y)^3+b\cdot f_c(x,y)^2+c\cdot f_c(x,y) +d \\ \end{aligned} \tag{14} \]

在该等式中，后缀“\(_c\)”表示相机伽马域中的值。因此，\(f_c(x,y)\)和\(p_c(f_c(x,y))\)表示相机伽马域中的基本色调映射曲线的输入亮度和输出亮度。然后，\(t_c\)表示在同一域中将曲线从线性切换到三次的阈值。为了确定它们的系数，我们施加的条件，在阈值电平和最大输入电平的合成亮度和一阶微分系数应该等于那些传统的拐点函数曲线。该约束描述如下，

\[p_c(t_c)=at_c^3+bt_c^2+ct_c+d=t_c \tag{15} \]

\[p_c'(t_c)=3at_c^2+2bt_c+c=1 \tag{16} \]

\[p_c(m_c)=am_c^3+bm_c^2+cm_c+d=1 \tag{17} \]

\[p_c'(m_c)=3am_c^2+2bm_c+c=s_c \tag{18} \]

其中，\(m_c\)表示最大输入电平，\(s_c\)表示最大输入电平处的传统拐点曲线的微分系数，描述为

\[s_c = \frac{1-k_c}{t_c-k_c} \tag{19} \]

其中，\(k_c\)表示在传统拐点曲线的拐点处的亮度级。通过求解\((15)-(18)\)，计算得到如下三次曲线的系数\(a,b,c,d\)。

\[a = \frac{(s_c-1)t_c+(2-m_c-m_cs_c)}{(t_c-m_c)^3} \tag{20} \]

\[b=\frac{2(1-s_c)t_c^2+(m_cs_c+2m_c-3)(t_c+m_c)}{(t_c-m_c)^3} \tag{21} \]

\[c=\frac{s_ct_c^3+(s_c-4)m_ct_c^2+(6-m_c-2m_cs_c)m_ct_c-m_c^3}{(t_-m_c)^3} \tag{22} \]

\[d=\frac{(1-m_cs_c)t_c^3+(m_cs_c+2m_c-3)m_ct_c^2}{(t_c-m_c)^3} \tag{23} \]

图4显示了与传统拐点曲线近似的色调映射曲线。在该图中，示出了\(m_c=2.0,k_c =0.9\)的常规拐点曲线。此外，还示出了\(t_c=0.15,0.25,0.35,0.45,0.55,0.65\)时的六种近似拐点曲线。如图4所示，在阈值电平和最大输入电平下，近似拐点曲线与传统拐点曲线平滑连接。此外，它表明，阈值越接近拐点，阴影到中间亮度的范围转换越接近传统的拐点曲线。然而，如果阈值电平设置得太大，例如\(t>0.35\)，则近似拐点曲线超过传统拐点曲线。当它具有比常规拐点曲线大的输出时，即使应用LCRT，也变得难以再现具有高对比度的高亮区域。 因此，我们应该通过实验选择最大阈值，而不会过冲。

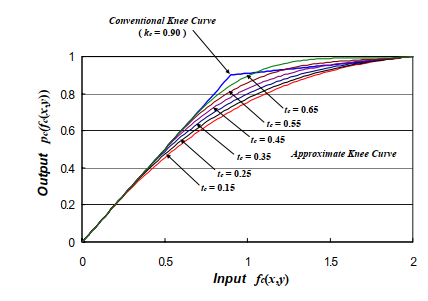
图4 传统和近似拐点曲线

B.LCRT在拐点曲线拟合中的应用

等式\((14)\)表示相机伽马域中的输入亮度和输出亮度之间的关系。这些方程在亮度域中变换如下，

\[\begin{aligned} &if(f(x,y)<t) \\ &\qquad p\big(f(x,y) \big)=f(x,y) \\ &else \\ &\qquad p\big(f(x,y) \big)= \{a\cdot f(x,y)^3+b\cdot f(x,y)^2+c\cdot f(x,y) +d \}^\gamma \end{aligned} \tag{24} \]

其中，\(\gamma\)表示照相机\(\gamma\)，并且\(a,b,c,d\)由\((20)\)至\((23)\)给出。此外，\(t\)表示阈值，由$t=t_c^\gamma \(计算。\)(24)$的微分函数描述如下。

\[\begin{aligned} &if(f(x,y)<t) \\ &\qquad \frac{dp\big(f(x,y) \big)}{df(x,y)}=1 \\ &else \\ &\qquad \frac{dp\big(f(x,y) \big)}{df(x,y)}=\gamma \times \{a\cdot f(x,y)^3+b\cdot f(x,y)^2+c\cdot f(x,y) +d \}^{\gamma - 1} \\ &\qquad\qquad\qquad\qquad \times \{3a\cdot f(x,y)^2+2b\cdot f(x,y)+c\} \end{aligned} \tag{25} \]

一旦确定了近似拐点曲线，就可以通过用\((24)\)和\((25)\)代替\((9)\)和\((10)\)来对其应用LCRT过程。这是我们提出的数字摄像机动态范围压缩算法。

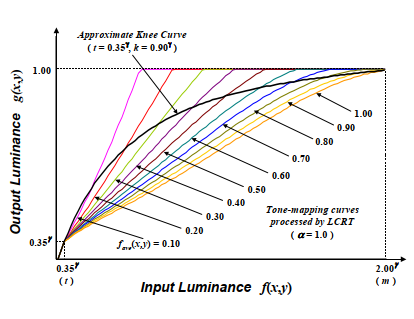
图5 LCRT处理的近似拐点曲线

图5示出了LCRT处理的近似拐点曲线和色调映射曲线。在这种情况下，参数分别设置为$\gamma =2.2,m=2.0^\gamma,k=0.9^\gamma,t=0.35^\gamma,\alpha =1.0$。该图说明了$f(x,y)= 0.1 $到$ 1.0$的$10$种情况下曲线的变化。如该图所示，由于亮度范围没有被近似拐点曲线压缩，所以阈值水平下的局部对比度没有被LCRT增强。另一方面，超过阈值的色调范围根据三次曲线被压缩，因此局部对比度被增强以保持与原始对比度相同。因此，在该范围内，取决于局部平均值的不同，不同的色调映射曲线被应用于不同像素。然而，当输入亮度大于局部平均值时，该过程倾向于导致饱和亮度，因为拐点以上的输出色调范围不够宽。所以在这种情况下应当将增益参数$\alpha $设置小于$1.0$。这里，为了补偿视觉对比度的劣化，当输入亮度小于局部平均值时，通过将增益参数$\alpha $设置大于$1.0$来放大局部对比度增益。

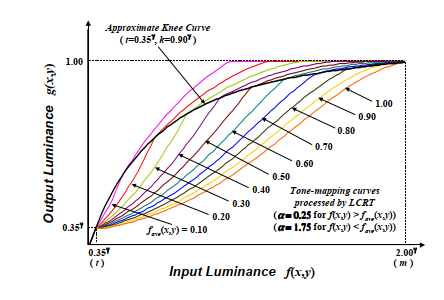
图6 应用不同 α 色调映射曲线

图6示出了如下确定$\alpha $的情况下的色调映射曲线， $$ \begin{aligned} &if(f(x,y)>f_{ave}(x,y)) \\ &\qquad \alpha=0.25 \\ &else \\ &\qquad \alpha=1.75 \end{aligned} \tag{26} $$ 从图中可以看出，通过该调整，亮度几乎不饱和。

另外，应当注意，输出亮度没有色调跳跃，因为近似拐点曲线保证了在任何亮度水平下输出水平和一阶微分系数两者的连续性。

C.系统

图7总结了所提出的算法。我们的算法在亮度域操作，同最传统的动态范围压缩方法一致。因此，首先将捕获的RGB图像变换为亮度分量Y。接下来，通过将近似拐点曲线应用于亮度分量Y来计算基本色调映射图像FT。同时，使用例如高斯滤波器的空间平均滤波器卷积到亮度分量Y以计算得到像素周围的局部平均LA。根据\((10)\)，计算局部对比度增益CG以保持与原始的局部对比度一样多的局部对比度。然后，将基本色调映射图像FT乘以局部对比度增益CG，我们得到LDR亮度分量LD。最后，通过LDR亮度分量LD与输入亮度分量Y的比率来修改捕获图像的RGB通道，计算得到的RGB图像。

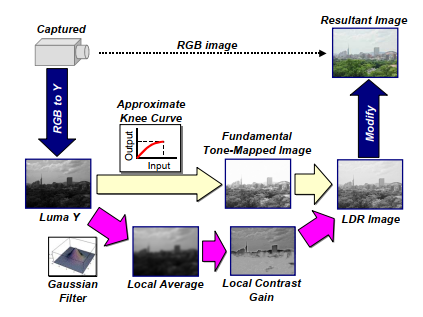
图7 本文算法完整系统

IV.实验结果

我们测试了我们提出的算法的性能。在这个实验中，我们使用的数码相机富士Finepix F710，以捕捉高动态范围的图像。这款相机有两个传感器，S(敏感)和R(范围)传感器，彼此相邻。S传感器就像普通传感器一样，R传感器灵敏度较低，并扩展了捕捉照片明暗的能力。首先，我们校准了这两个传感器。然后，我们将S和R传感器捕获的图像进行合成，以获得HDR图像用于我们的实验。最后，我们将我们提出的算法应用于HDR图像，并评估了性能。

A.校准

首先，对S和R传感器的灵敏度进行标定。在这个实验中，我们捕获了投影在屏幕上的测试图案，并比较了由两个传感器获得的图像，我们分别称之为“S图像”和“R图像”。图8示出了由S传感器捕获的图像。

图8 S传感器拍摄图像

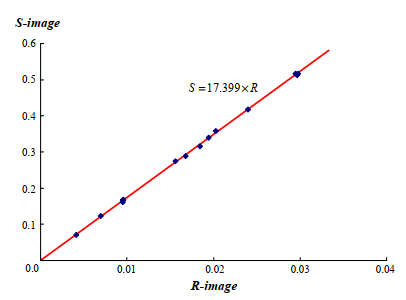
图9 S和R传感器拍摄图像的关系

然后我们计算每个补丁的平均亮度，并绘制“S图像”和“R图像”的相应亮度之间的关系，如图9所示。该图说明两个传感器的灵敏度具有由以下线性方程近似的比例关系，

\[S(x,y)=17.399\times R(x,y) \tag{27} \]

其中\(S(x,y)\)和\(R(x,y)\)分别表示“S图像”和“R图像”中的像素级。因此，我们合成具有如下混合比率的图像，

\[\begin{aligned} &if(S(x,y)<th0) \\ &\qquad f(x,y)=S(x,y) \\ &else if(S(x,y)<thr1)\\ &\qquad f(x,y)=\frac{thr1-S(x,y)}{thr1-thr0}\times S(x,y)+ \frac{S(x,y)-thr0}{thr1-thr0}\times 1.7399\times R(x,y) \\ &else \\ &\qquad f(x,y)=17.399\times R(x,y) \\ \end{aligned} \tag{28} \]

其中，\(th0\)和\(th1\)表示用于构成“S图像”和“R图像”的阈值。“S图像”和“R图像”的混合比如图10所示。

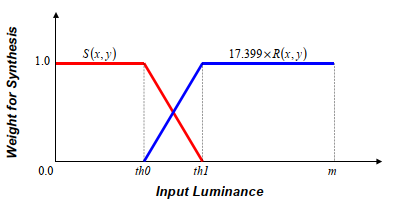
图10 S和R传感器拍摄图像混合比例

在下面的实验中，我们设置\(th0=0.8\)和\(th1=0.9\)来合成HDR图像。
此外，我们设置HDR图像\(f(x,y)\)的上限。一般来说，没有多量程传感器的普通数码摄像机无法拍摄像Finepix F710这样的HDR图像。因此，我们将所计算的HDR图像亮度\(f(x,y)\)裁剪为输出LDR图像亮度\(g(x,y)\)的\(4.6\)倍高，这导致\(m=2.0^\gamma\)。

B.实验结果对比

我们对许多测试图像进行了实验。在这个实验中，我们设置了如图6所示的相同参数。图11、图12和图13中示出了一些结果。每个图中的顶部、中部和底部行分别说明了全输入范围、近似拐点曲线和所提出算法的线性压缩处理结果。

图11 实验结果1

图12 实验结果2

图13 实验结果3

如图清楚地示出的，线性范围压缩(顶行)非常好地保持了高光对比度，但是再现了如在面部区域中看到的阴影中的中等范围亮度。因此，这些不是好的结果，因为拍摄图像中的主要对象没有被清楚地再现，并且没有充分反映摄影者的意图。相反，近似拐点曲线(中间行)清楚地再现阴影到中间范围亮度，使得它们在这方面优于顶部行。然而，例如，在图11(B)中的窗口外部、图12(B)中的蓝天和白色、或图13(B)中的显示面板中，这些结果中的高光对比度严重降低。这些结果与直接观察到的现象有很大的不同。

而另一方面，在我们提出的算法的结果(底部行)中，高亮对比度高度保持，同时清晰地再现阴影到中间范围亮度。这些都与直接观察有密切的关系。

V.结论和将来的工作

本文提出了一种新的数字摄像机动态范围压缩方法。该算法与传统的空间变化方法一样，基于视觉对比度依赖于局部图像对比度的假设。该方法还具有满足数字摄像机不将阴影变为中间范围外观的要求的特点。

首先，我们提出了一种新的算子LCRT，它根据基本色调映射曲线自动自适应地增强局部图像对比度，并在任何亮度水平下保持与原始图像相同的局部对比度。其次，我们定义了一个近似的拐点曲线，保证在任何亮度水平的输出电平和一阶微分系数的连续性，保持功能接近传统的拐点曲线。然后，我们所提出的算法的动态范围压缩制定应用LCRT的近似拐点曲线。

实验结果证明了该算法的性能。这些结果表明，该算法保留了亮区的局部对比度，如天空区域或通过窗口看到的外部场景，而不会降低阴影到中间范围亮度，包括主要对象，如面部区域。

该算法有许多参数，但大多数参数是根据给定的基本色调映射曲线自动确定的。因此，我们只需要实验确定几个参数。

将该方法应用于数字摄像机的动态范围压缩，可以轻松再现任何亮度水平下的高对比度的真实图像。然而，目前所提出的算法需要很高的计算成本与大量的内存。算法的更有效的实现留给我们未来的工作。

附录

在本附录中，我们从\((3)\)导出\((6)\)和\((7)\)。如上所述，F(x,y)、F(x,y)、G(x,y)和G(x,y)分别表示f(x,y)、f(x,y)、g(x,y)和g(x,y)的对数值。这些关系描述如下。

\[\begin{aligned} &F(x,y)=log\{f(x,y) \} \\ &F_{ave}(x,y)=log\{f_{ave}(x,y) \} \\ &G_(x,y)=log\{g(x,y) \} \\ &G_{ave}(x,y)=log\{g_{ave}(x,y) \} \\ \end{aligned} \tag{A1} \]

此外，\(P\big(F(x,y)\big)\) 表示\(p\big(f(x,y)\big)\)的双对数方程。其描述如下。

\[P\big(F(x,y)\big)=log(p\big(f(x,y)\big)) \tag{A2} \]

通过将\((A1)\)和\((A2)\)代入相应的项，等式\((3)\)可以重写如下。

\[\begin{aligned} &log\Big\{g(x,y) \Big\} \\ &=log\{p\big(f(x,y)\big)\} \\ & \qquad + \Bigg\{1-\frac{dP\big(F(x,y)\big)}{dF(x,y)} \Bigg\}\cdot \Big\{log\{f(x,y) \}-log\{f_{ave}(x,y) \} \Big\} \\ & =log\Big\{p\big(f(x,y)\big)\Big\}+log\Bigg\{\Big(\frac{f(x,y)}{f_{ave}(x,y)}\Big)^{\Big\{1-\frac{dP(F(x,y))}{dF(x,y)} \Big\}} \Bigg\} \\ &=log\Bigg\{p\big(f(x,y)\big)\cdot \Big(\frac{f(x,y)}{f_{ave}(x,y)}\Big)^{\Big\{1-\frac{dP(F(x,y))}{dF(x,y)} \Big\}} \Bigg\} \end{aligned} \tag{A3} \]

等式\((A3)\)导致以下等式。

\[g(x,y) = p\big(f(x,y)\big)\cdot \Big(\frac{f(x,y)}{f_{ave}(x,y)}\Big)^{\Big\{1-\frac{dP(F(x,y))}{dF(x,y)} \Big\}} \tag{A4} \]

这里，双对数域中的基本色调映射曲线的导数可以如下变换到亮度域。

\[\begin{aligned} &\frac{dP(F(x,y))}{dF(x,y)} \\ &=\frac{d\{log\{p(f(x,y))\}\}}{d\{log\{f(x,y)\}\}} \\ &=\Bigg\{\frac{d\{log\{p(f(x,y))\}\}}{df(x,y)} \Bigg\}\Bigg/ \Bigg\{\frac{d\{log\{f(x,y)\}\}}{df(x,y)} \Bigg\} \\ &= \Bigg\{\frac{d\{log\{p(f(x,y))\}\}}{dp\{f(x,y)\}} \Bigg\} \cdot \Bigg\{\frac{dp\{f(x,y)\}}{df(x,y)} \Bigg\}\Bigg/ \Bigg\{\frac{d\{log\{f(x,y)\}\}}{df(x,y)} \Bigg\} \\ &=\Bigg\{\frac{1}{dp\{f(x,y)\}}\Bigg\} \cdot \Bigg\{\frac{dp\{f(x,y)\}}{df(x,y)} \Bigg\} \Bigg/ \Bigg\{\frac{1}{f(x,y)} \Bigg\} \\ &=\frac{f(x,y)}{ p\big(f(x,y)\big)}\cdot\frac{dp\big(f(x,y)\big)}{df(x,y)} \end{aligned} \tag{A5} \]

因此，通过用\((A5)\)代替\((A4)\)来导出等式\((6)\)。