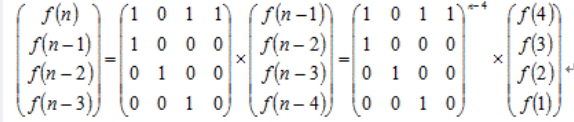『模拟赛』暑假集训CSP提高模拟25

news/2024/9/21 8:11:41/文章来源:https://www.cnblogs.com/Ratio-Yinyue1007/p/18370366

Rank

学新东西，不算挂分（确信。

A. 可持久化线段树

原板子[SP11470] TTM - To the moon

主席树，不过区间修改。

赛时想到标记永久化了，不过打 pushdown 的时候没新开点，于是 -100pts。

还挺简单的，建树和更改动态开点，按线段树来，加个 lazy，其他的就是普通线段树的操作。

板子

#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
#define fu(x,y,z) for(register int (x)=(y);(x)>=(z);(x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch=getchar();lx x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);return x*f;
}
#undef lx
#define qr qr()
#define fi first
#define se second
const int Ratio=0;
const int N=3e5+5;
const int mod=998244353;
int n,m,cnt;
int a[N],rot[N];
int son[N*32][2];
ll v[N*32],lazy[N*32];
namespace Wisadel
{#define ls (son[rt][0])#define rs (son[rt][1])#define mid ((l+r)>>1)int Wclone(int rt){son[++cnt][0]=son[rt][0];son[cnt][1]=son[rt][1];v[cnt]=v[rt];lazy[cnt]=lazy[rt];return cnt;}void Wpushup(int rt){v[rt]=(v[ls]+v[rs])%mod;}void Wpushdown(int rt,int l,int r){ls=Wclone(ls),rs=Wclone(rs);lazy[ls]=(lazy[ls]+lazy[rt])%mod;lazy[rs]=(lazy[rs]+lazy[rt])%mod;v[ls]=(v[ls]+lazy[rt]*(((l+r)>>1)-l+1)%mod+mod)%mod;v[rs]=(v[rs]+lazy[rt]*(r-((l+r)>>1))%mod+mod)%mod;lazy[rt]=0;}int Wbuild(int rt,int l,int r){rt=++cnt;if(l==r){v[rt]=a[l];return rt;}ls=Wbuild(ls,l,mid),rs=Wbuild(rs,mid+1,r);Wpushup(rt);return rt;}int Wupd(int rt,int l,int r,int x,int y,int va){rt=Wclone(rt);if(x<=l&&r<=y){lazy[rt]=(lazy[rt]+va)%mod;v[rt]=(v[rt]+1ll*(r-l+1)*va%mod+mod)%mod;return rt;}if(lazy[rt]) Wpushdown(rt,l,r);if(x<=mid) ls=Wupd(ls,l,mid,x,y,va);if(y>mid) rs=Wupd(rs,mid+1,r,x,y,va);Wpushup(rt);return rt;}int Wq(int rt,int l,int r,int x,int y){if(x<=l&&r<=y) return v[rt];if(lazy[rt]) Wpushdown(rt,l,r);ll res=0;if(x<=mid) res+=Wq(ls,l,mid,x,y);if(y>mid) res=(res+Wq(rs,mid+1,r,x,y))%mod;return res%mod;}short main(){// freopen(".in","r",stdin),freopen(".out","w",stdout);n=qr,m=qr;fo(i,1,n) a[i]=qr;rot[0]=Wbuild(1,1,n);int tim=0;fo(i,1,m){int op=qr,x=qr,y,va;if(op==1) y=qr,va=qr,rot[++tim]=Wupd(rot[tim],1,n,x,y,va);else if(op==2) y=qr,printf("%d\n",Wq(rot[tim],1,n,x,y));else tim-=x;}return Ratio;}
}
int main(){return Wisadel::main();}

B. Little Busters !

签，不过 Tarjan。~~跟 Tarjan 真心不熟~~

赛时暴力寄寄，拿了特殊性质 40pts。

考虑正解，记下每种边，开局只连 lun 边，跑 Tarjan 找边双，边的两端点在同一边双就计入答案，然后考虑 qie 边，两端点不在同一边双就计入答案并将两边双合并，最后判断边双数量是否为 1，输出答案即可。

~~加练 Tarjan！~~

点击查看代码

#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
#define fu(x,y,z) for(register int (x)=(y);(x)>=(z);(x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch=getchar();lx x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);return x*f;
}
#undef lx
#define qr qr()
#define fi first
#define se second
const int Ratio=0;
const int N=2e5+5;
const int mod=998244353;
int n,m;
int hh[N],to[N<<1],ne[N<<1],cnt;
int dfn[N],low[N],tot,sccnt,ins[N],bl[N],fx[N];
vector<pair<int,int> >ans,lun,qie;
stack<int>s;
namespace Wisadel
{inline int Wfind(int x){return fx[x]==x?x:fx[x]=Wfind(fx[x]);}void Wadd(int u,int v){to[++cnt]=v;ne[cnt]=hh[u];hh[u]=cnt;}void Wtarjan(int u,int fa){dfn[u]=low[u]=++tot;ins[u]=1;s.push(u);for(int i=hh[u];i!=-1;i=ne[i]){int v=to[i];if(v==fa) continue;if(!dfn[v])Wtarjan(v,u),low[u]=min(low[u],low[v]);else if(ins[v]==1) low[u]=min(low[u],dfn[v]);}if(dfn[u]==low[u]){int k=0;sccnt++;while(u!=k){k=s.top();s.pop();ins[k]=0;bl[k]=sccnt;}}}void Wmerge(int x,int y,int id){x=Wfind(x),y=Wfind(y);if(x!=y){ans.push_back(qie[id]);fx[y]=x;sccnt--;}}short main(){n=qr,m=qr;memset(hh,-1,sizeof hh);fo(i,1,m){int a=qr,b=qr;string s;cin>>s;if(s=="Lun") Wadd(a,b),Wadd(b,a),lun.push_back(make_pair(a,b));if(s=="Qie") qie.push_back(make_pair(a,b));}fo(i,1,n){if(!dfn[i]) Wtarjan(i,0);fx[i]=i;}fo(i,0,(int)lun.size()-1)if(bl[lun[i].fi]==bl[lun[i].se]) ans.push_back(lun[i]);fo(i,0,(int)qie.size()-1)if(bl[qie[i].fi]!=bl[qie[i].se]) Wmerge(bl[qie[i].fi],bl[qie[i].se],i);if(sccnt!=1) printf("NO\n");else{printf("YES\n%d\n",ans.size());fo(i,0,ans.size()-1)printf("%d %d\n",ans[i].fi,ans[i].se);}return Ratio;}
}
int main(){return Wisadel::main();}

C. 魔卡少女樱

[ABC276G] Count Sequences

计数题。

赛时打表拿了 45pts，感觉还行。

考虑正解。由于相邻两数模 3 意义下不同余，所以考虑差分，记下相邻两数差模 3 的值，显然不能为 0，因此只有 1 和 2 两种可能。当然可以在查分数组中插入 3，仍能保证合法。我们枚举这里面 2 的个数，再根据差分的性质：和为序列最后的数，即和 \(\le m\)，可以求得最多插入 3 的个数，进而总和成答案。

具体见下（有点漏洞，比如这里没有算上开始枚举的 \(a_1\) 即差分数组中第一个数的值）：

点击查看代码

#include<bits/stdc++.h>
#define fo(x,y,z) for(register int (x)=(y);(x)<=(z);(x)++)
#define fu(x,y,z) for(register int (x)=(y);(x)>=(z);(x)--)
using namespace std;
typedef long long ll;
#define lx ll
inline lx qr()
{char ch=getchar();lx x=0,f=1;for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') f=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=(x<<3)+(x<<1)+(ch^48);return x*f;
}
#undef lx
#define qr qr()
#define fi first
#define se second
const int Ratio=0;
const int N=2e7+5;
const int mod=998244353;
int n,m;
ll jc[N],ny[N],sum[N],ans;
namespace Wisadel
{ll Wqp(ll x,int y){ll res=1;while(y){if(y&1) res=res*x%mod; x=x*x%mod; y>>=1;}return res;}ll C(int n,int m){if(n>m) return 0;if(!n) return 1;return jc[m]*ny[m-n]%mod*ny[n]%mod;}short main(){n=qr,m=qr;jc[0]=sum[0]=ny[0]=1;fo(i,1,N-3) jc[i]=jc[i-1]*i%mod;ny[N-3]=Wqp(jc[N-3],mod-2);fu(i,N-4,1) ny[i]=ny[i+1]*(i+1)%mod;fo(i,1,m-1) sum[i]=(sum[i-1]+C(n-1,n+i-1))%mod;fo(i,0,2)for(int j=0;j<n&&j+n-1+i<=m;j++)ans=(ans+C(j,n-1)*sum[(m-j-n+1-i)/3]%mod+mod)%mod;printf("%lld\n",ans);return Ratio;}
}
int main(){return Wisadel::main();}