从高斯消元法到特征值特征向量

摘要：

帮助具有特征值和特征向量等线性代数的基础概念但不能理解其意义的读者理解特征值和特征向量出现的意义。从高斯消元法到矩阵乘法、用矩阵乘法的两套解释逻辑解释相似矩阵，用相似矩阵解释特征值和特征向量。

正文：

1.从高斯消元法到矩阵乘法-矩阵是如何产生的

注：这段内容引自：马同学 (matongxue.com)

高斯消元法产生于对线性方程组，即多元一次方程组的求解问题。这里只考虑有唯一解的情况。操作是通过行之间的线性组合（相互加减）使对角线以外的系数为零。以下图为例

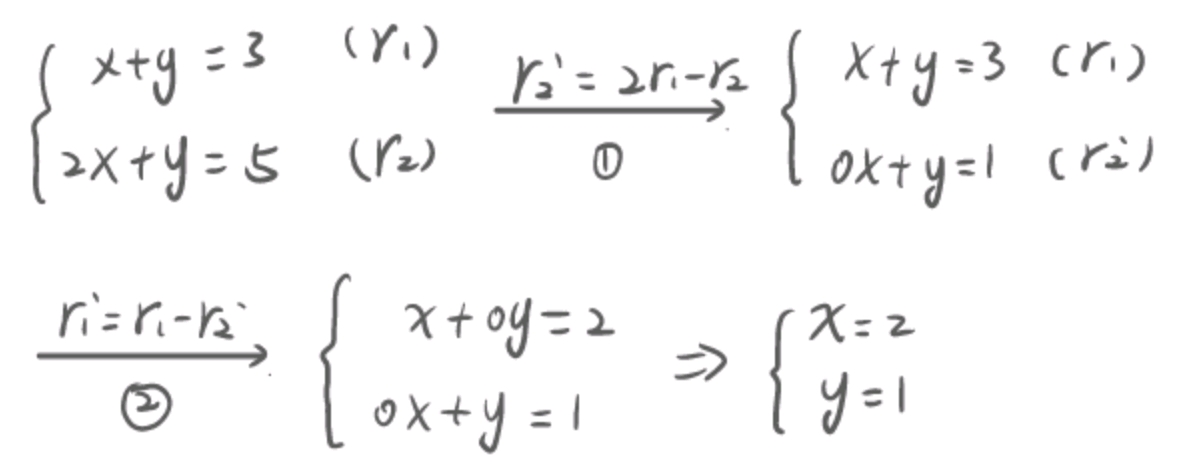
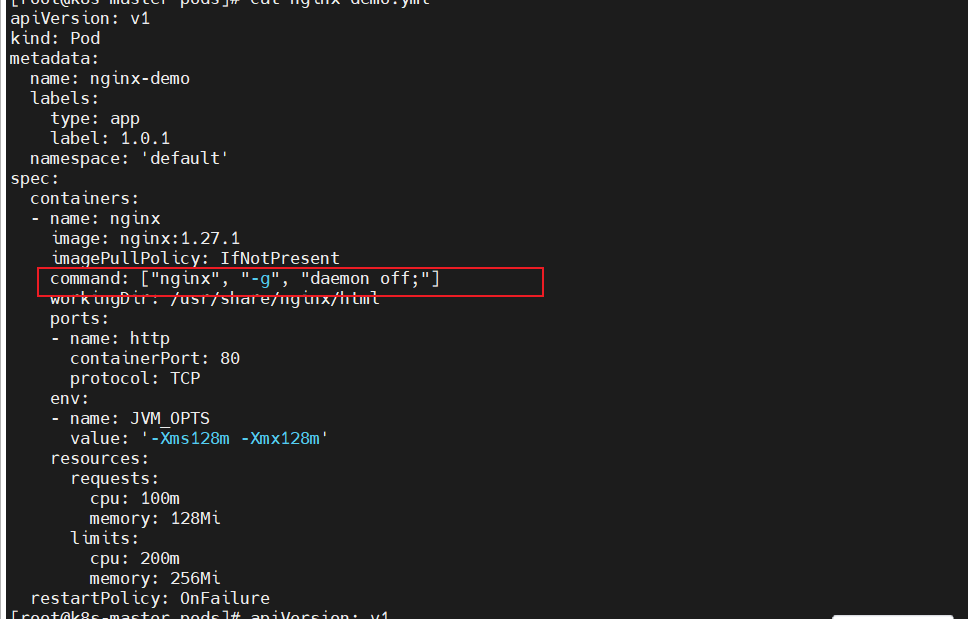
英国数学家阿瑟·凯莱（1821－1895）将高斯消元方法符号化，提出了数块和数块乘法。将线性代数写成数块的形式

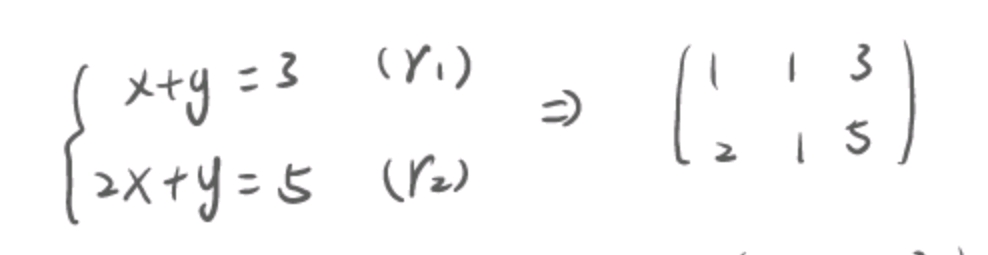
将行之间的线性组合写成为数块乘法形式，单行乘法表示第一步

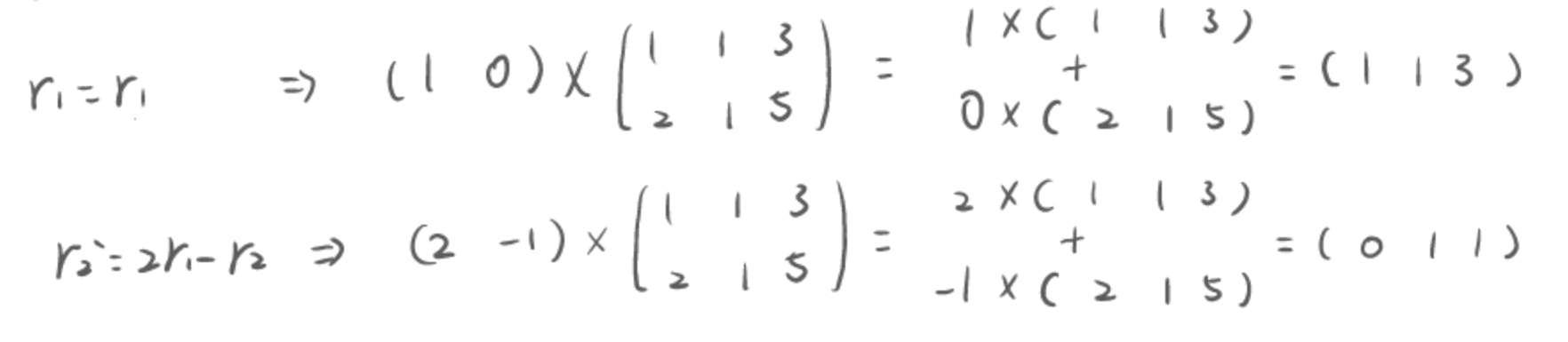
将单行乘法合并为多行乘法表示整个消元过程得到减化

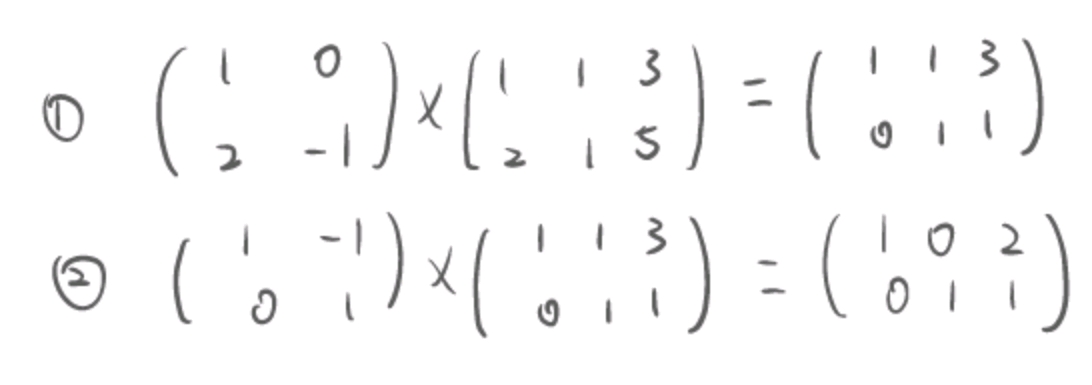
后将数块定义为了矩阵，以上就是矩阵及矩阵乘法是如何产生的。

2.矩阵乘法的两套解释逻辑

注：这段内容引自：马同学 (matongxue.com)

用两套逻辑解释下面这个矩阵乘法等式：

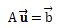
2.1逻辑1：矩阵是一种变换

可以将矩阵A理解为是一种变换，向量u经过矩阵A变换后得到向量b。

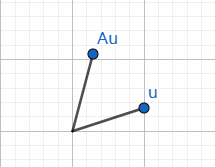
 2.2逻辑2：矩阵的列构成基向量组，向量是基向量坐标系下的坐标

 向量a的位置是确定的，但在不同坐标系下a的坐标不同。比如向量a在(1,0),(0,1)为基向量的坐标系中坐标为(4,3)，在(4,0),(0,3)为基向量的坐标系中坐标为(1,1)。基向量构成矩阵的列，坐标构成向量，得到矩阵：

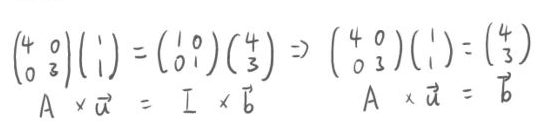
这里先认为向量a在(1,0),(0,1)为基向量的坐标系中坐标为a的绝对坐标。由于a的位置是始终没有变的，所以在任何的坐标系（比如说A）下a的相对坐标（比如说u）可能不同，但a的绝对坐标（比如说b）始终不变。换句话说，一个向量（或者说是一个点）在矩阵A的坐标系下的坐标就是在A的基向量的线性组合，这个线性组合等效于这个向量本身。通过代入基向量的绝对坐标表示形式就得到向量的绝对坐标。

3.用矩阵乘法解释相似矩阵

注：这段内容引自：马同学 (matongxue.com)

首先给出相似矩阵的物理意义：在相对坐标系中的变换等效于在绝对坐标系中的变换，此时成这两个变换是相似矩阵。数学意义：设A,B都是n阶矩阵，若有可逆矩阵P，使

 则称B是A的相似矩阵，或说A和B相似 ---《线性代数》同济版

数学定义中矩阵P就是相对坐标系，矩阵A就是在相对坐标系中的变化，矩阵B就是在绝对坐标系中的变换。

现在具体解释为什么？

向量u在绝对坐标系中的坐标就是u，在相对坐标系P中的坐标是v,于是有下面这个等式

在相对坐标系下对向量u做变换A，变换后的得到新的向量，新的向量的相对坐标为w，于是有下面这个等式

上式中P是相对坐标系，A是在相对坐标系下的变换，v是变换前的相对坐标，所以等号两边为变换后新的向量的绝对坐标。

在绝对坐标系下对向量u做变换B，变化后得到新的向量，新的向量的绝对坐标为z，于是有下面这个等式

上式中I是绝对坐标系，是单位矩阵，所以可以省略。

让在相对坐标系P中的变换A与在绝对坐标系I中的变换B等效，及让新向量的绝对坐标相同，于是有下面这个等式

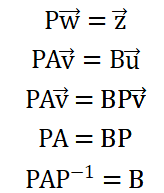
 所以A在相对坐标系P中的变化，B是与之等效的在绝对坐标系的变换。应用于用相对坐标系P中的简单变换A来描述绝对坐标系中的复杂变换B。

4.用相似矩阵解释特征值和特征向量

注：这段内容引自：马同学 (matongxue.com)

特征值和特征向量的定义是：矩阵A，有向量v和标量λ满足：

 则向量v为A的特征向量，标量λ为A的特征值。eigenvalue之所以翻译为特征值是因为eigen在德语中是固有的，而这个特性只有矩阵A自身有关。

这里只考虑n*n矩阵A，有n个特征向量v和n个特征值λ满足的情况。所有的特征向量作为列向量组成特征矩阵V，对应的特征值作为对角元素构成一个对角矩阵。于是有下面的式子

用相似矩阵解释，把矩阵Σ作为变换，Σ就是A的相似矩阵。由于Σ是对角矩阵，相当于在每一个基向量上进行伸缩，伸缩的倍数就是对应的特征值。就是用在A的特征向量作为基向量构成的相对坐标系V中简单伸缩变换描述在绝对坐标系中的复杂变换A。

 

5.特征值和特征向量的应用

注：这段内容引自：马同学 (matongxue.com)和特征值和特征向量到底是个啥？能做什么用？ - marsggbo - 博客园 (cnblogs.com)

现在有变换A，原向量u(1,1)

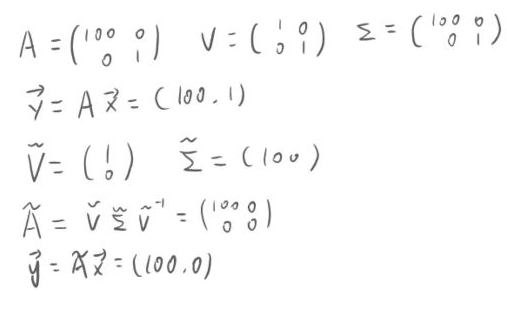
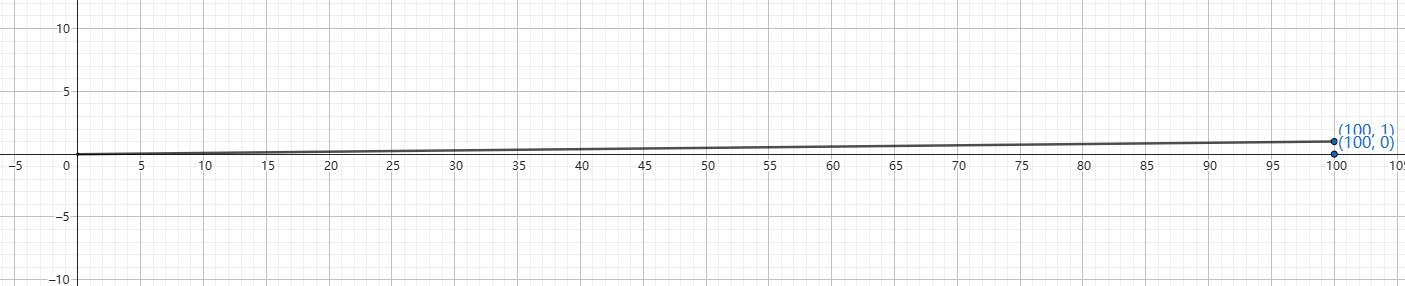
V是A的特征矩阵，Σ是特征值。变换A是在第一个特征向量方向上放大100倍，在第二个特征向量方向上保持不变，变换后向量y为(100,1)。由于第二个特征方向上变化相对第一个方向上太小了，第一个方向上的变换就足够表现变换的特性，所以考虑省去第二个特征方向和第二个特征值后得到变化A的近似，近似变换后的向量为(100,0)。从而通过略去变化小的部分，减小矩阵V和Σ的大小从而压缩数据。

到这里已经结束，最后特征向量是否正交的问题还会产生出奇异值分解方法的概念，这是之后的内容。

写这篇博客的目的：自己在学习SVD过程中总会遇到特征值和特征向量的概念，但起初对特征值和特征向量的真正意义一直无法理解。 “遇到一个数学概念，先问自己三个问题，第一个问题是这个概念是由哪个问题延伸出来的”，以上就是我自己后来通过阅读他人分享的资料后的自己对特征值和特征向量的意义的笔记和理解。希望能对和我有过同样疑问的同学有所帮助。如有错误欢迎批评指正，邮箱pengh0328@gmail.com。