【Python脚本】刚度矩阵格式转换

对于1-2-3坐标系:

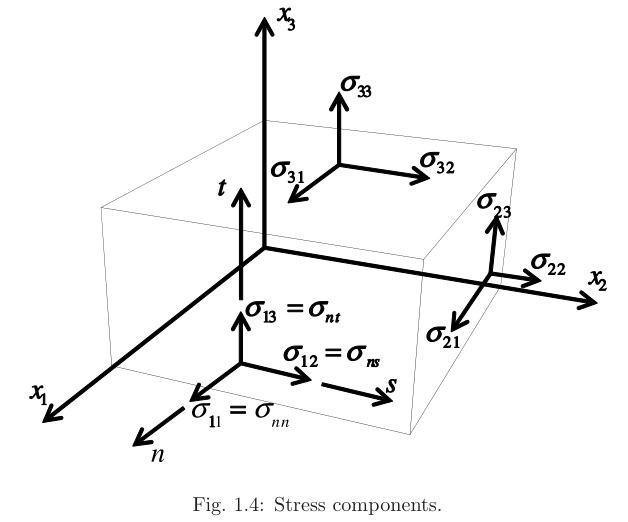
应力矩阵如下:

\[\left.[\sigma]=\left[\begin{array}{ccc}\sigma_{11}&\sigma_{12}&\sigma_{13}\\\sigma_{12}&\sigma_{22}&\sigma_{23}\\\sigma_{13}&\sigma_{23}&\sigma_{33}\end{array}\right.\right] \]

张量应变矩阵如下:

\[\left.[\varepsilon]=\left[\begin{array}{ccc}\varepsilon_{11}&\varepsilon_{12}&\varepsilon_{13}\\\varepsilon_{12}&\varepsilon_{22}&\varepsilon_{23}\\\varepsilon_{13}&\varepsilon_{23}&\varepsilon_{33}\end{array}\right.\right] \]

工程剪应变\(\gamma=2*\varepsilon\)

实际使用中会写成向量的形式:

\[应力向量\boldsymbol{\sigma}=[\sigma_{1} \qquad \sigma_{2} \qquad \sigma_{3} \qquad \sigma_{4} \qquad \sigma_{5} \qquad \sigma_{6}] \]

\[应变向量\boldsymbol{\epsilon}=[\epsilon_{1} \qquad \epsilon_{2} \qquad \epsilon_{3} \qquad \epsilon_{4} \qquad \epsilon_{5} \qquad \epsilon_{6}] \]

但是不同的商业软件,书籍中,应力/应变向量的含义并不完全一致,导致刚度柔度矩阵需要注意区分.