回溯part02-编程知识

回溯part02

news/2024/9/19 16:53:09/文章来源:https://www.cnblogs.com/yuehuaicnblogs/p/18374917

今天继续学习了回溯：

组合求和的进阶
元素可以重复使用：backtracking(candidates, target, sum, i); // 不用i+1了，表示可以重复读取当前的数
数组去重：首先数组排序，然后使用used
分割回文子串问题，抽象为组合问题，注意如何判断是否是回文子串

5. 39 组合总和（元素可重复使用）

题目：给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例：

输入：candidates = [2,3,6,7], target = 7,
所求解集为： [ [7], [2,2,3] ]

碰到组合的问题，回溯的一种，可以首先画树状图看看：

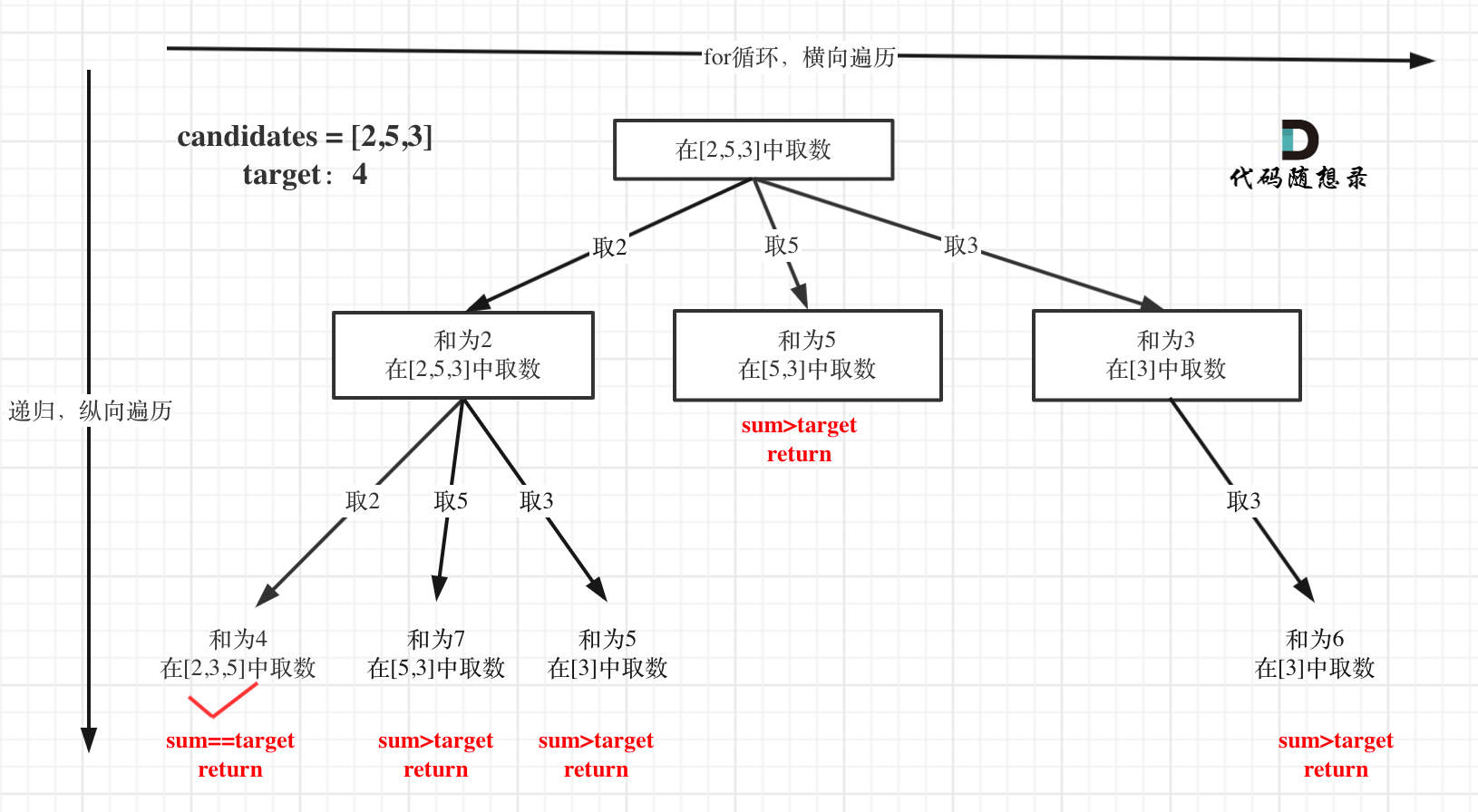
和之前组合的题目相比，可以重复取，但是这个重复，指的是当前的数可以再次用，而不是每个for循环都是从0到n。

若是for(int i=0;i<size;i++)，输出的错误结果是：[[2,2,3],[2,3,2],[3,2,2],[7]]，但是结果应该是[[2,2,3],[7]]。

需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？

如果是一个集合来求组合的话，就需要startIndex，例如：77.组合，216.组合总和III。

如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合。

画图之后，可以明显的看出叶子节点需要有=和>两个if，写少了就无限递归了。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum > target) {return;}if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i); // 不用i+1了，表示可以重复读取当前的数sum -= candidates[i];path.pop_back();}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();backtracking(candidates, target, 0, 0);return result;}
};

剪枝：

对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回。其实如果已经知道下一层的sum会大于target，就没有必要进入下一层递归了。

那么可以改for循环的搜索范围。对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。如图所示：

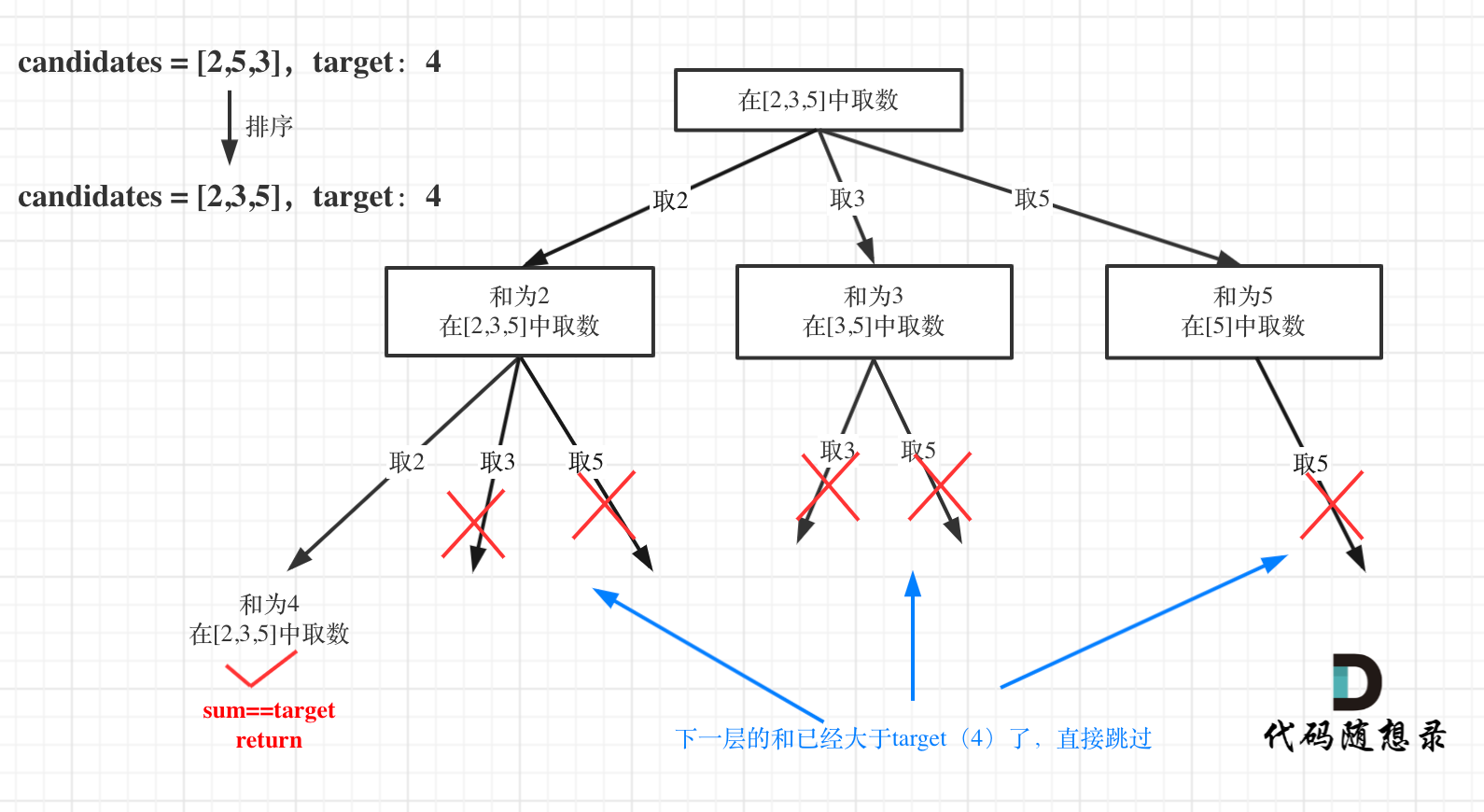
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)

时间复杂度：O(S)，其中 S 为所有可行解的长度之和。从分析给出的搜索树我们可以看出时间复杂度取决于搜索树所有叶子节点的深度之和，即所有可行解的长度之和。在这题中，我们很难给出一个比较紧的上界，我们知道 O(n×2 ^n)是一个比较松的上界，即在这份代码中，n 个位置每次考虑选或者不选，如果符合条件，就加入答案的时间代价。但是实际运行的时候，因为不可能所有的解都满足条件，递归的时候我们还会用 target−candidates[idx]≥0 进行剪枝，所以实际运行情况是远远小于这个上界的。
空间复杂度：O(target)。除答案数组外，空间复杂度取决于递归的栈深度，在最差情况下需要递归 O(target) 层。

6. 40 组合总和Ⅱ（数组去重）

题目：给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

和上一题39 组合总和的区别在于数组去重。39中candidates中的数字无重复，而且每个数字允许使用多次。所以假如结果是[1,2,2]，只能是2这个元素自己被使用了2次。所以不会有数组重复的问题。

但是此题，candidates中允许有重复数字，可能出现相同的数组，所以需要考虑数组去重。

数组去重问题，首先将candidates排序，方便比较是否元素相同

去重问题可以使用used，也可以不用

a. 使用used去重

要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

递归函数参数

与39 组合总和套路相同，此题还需要加一个bool型数组used，用来记录同一树枝上的元素是否使用过。

这个集合去重的重任就是used来完成的。

递归终止条件

与39 组合总和相同，终止条件为 sum > target 和 sum == target。

单层搜索的逻辑

这里与39.组合总和最大的不同就是要去重了。前面提到,,要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢?

在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过。说明是进入下一层递归，去下一个数，所以是树枝上。
used[i - 1] == false，说明同一树层candidates[i - 1]使用过。因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。

如图所示：

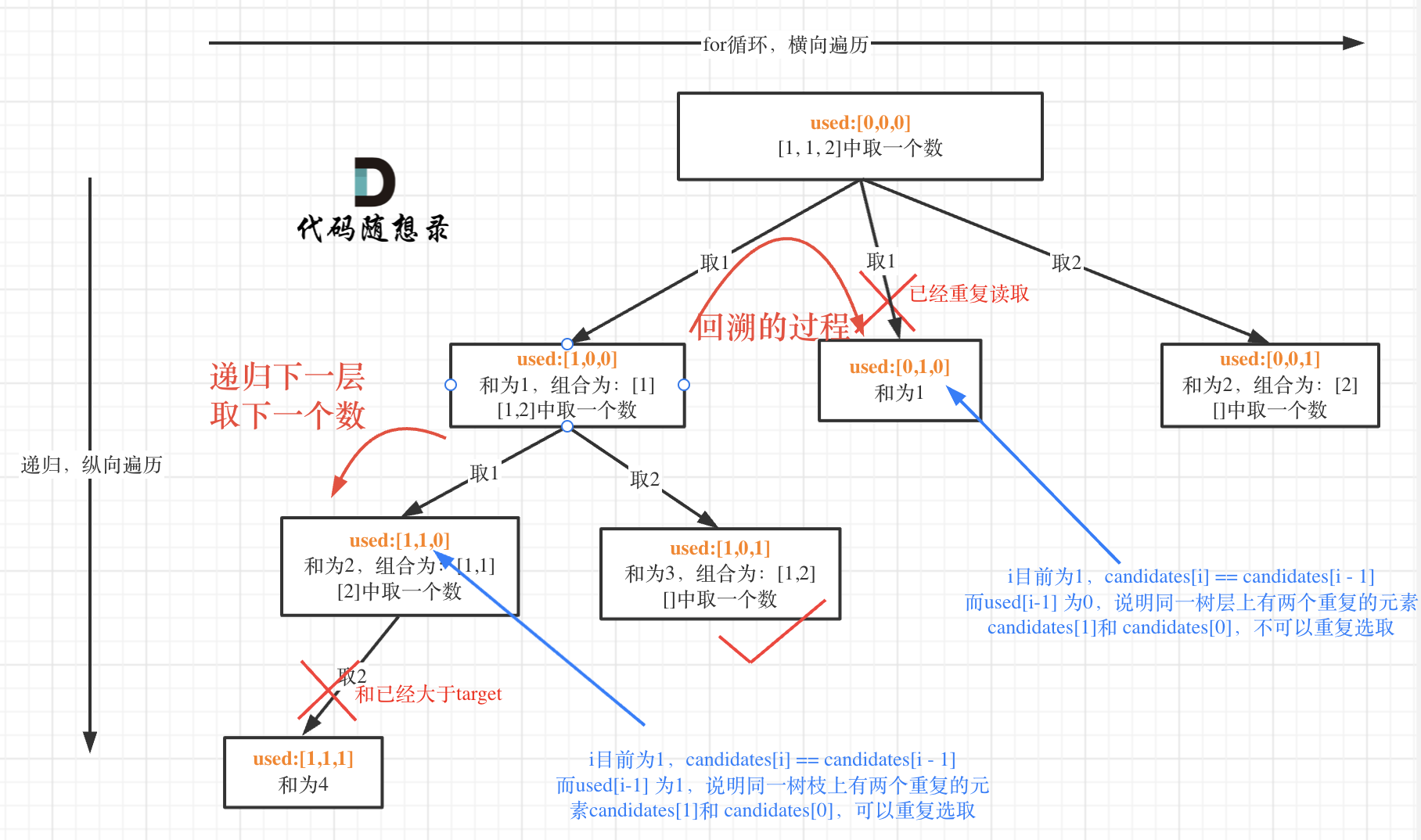
class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过// used[i - 1] == false，说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {continue;}sum += candidates[i];path.push_back(candidates[i]);used[i] = true;backtracking(candidates, target, sum, i + 1, used); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次used[i] = false;sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(), false);path.clear();result.clear();// 首先把给candidates排序，让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0, used);return result;}
};

时间复杂度: O(n * 2^n)
空间复杂度: O(n)

b. 使用`startIndex`去重

也可以不用used，用startIndex去重。关键就是这一句：if(i > start_index && candidates[i] == candidates[i - 1])continue;

例如1 1 2 5 6 7 10，在刚进入递归第一个数是1 有组合1 2 5 = 8 ，对应下标(0 2 3) 。以i=0的递归完，下标i=1 值为1不能再选了，要把它抛弃掉，要不然还会选到跟以下标i=0开始的组合。如1 2 5 对应下标(1 2 3)组合就重复了。题目要求不能有重复的组合，所以当前这层横向这个位置不能有相同的数。

class Solution {
private:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum == target) {result.push_back(path);return;}for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {// 要对同一树层使用过的元素进行跳过if (i > startIndex && candidates[i] == candidates[i - 1]) {continue;}sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i + 1); // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次sum -= candidates[i];path.pop_back();}}public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {path.clear();result.clear();// 首先把给candidates排序，让其相同的元素都挨在一起。sort(candidates.begin(), candidates.end());backtracking(candidates, target, 0, 0);return result;}
};

7. 分割回文串

题目：给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。返回 s 所有可能的分割方案。

示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]

a. 切割问题如何抽象为组合问题

可以自己画图看看，会发现切割掉开头的a后，需要处理剩下的字符串。这种方式和组合问题大同小异，既然如此，画树状图看看：

递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程差不多。

b. 回溯三部曲

递归函数参数

全局变量数组path存放切割后回文的子串，二维数组result存放结果集。

如何模拟那些切割线？其实就是指定下一个切割的起始位置，使用startIndex即可。
递归函数终止条件

从树形结构的图中可以看出：切割线切到了字符串最后面，说明找到了一种切割方法，此时就是本层递归的终止条件。

那么在代码里什么是切割线呢？startIndex，表示下一轮递归遍历的起始位置，就是切割线。所以终止条件是if (startIndex >= s.size())。
单层搜索的逻辑
- for循环中如何写？取决于每个节点有多少孩子。可以发现需要从startIndex开始遍历到字符串的最后，所以for (int i = startIndex; i < s.size(); i++)。
- 进入了每个for循环之后，需要处理节点，其实就是判断这个分割是不是构成了新的回文子串，是的话放到path中，不是就跳出去让i++。
- 然后接着递归。
- 接着回溯，将这个回文子串从path中弹出去。

c. 判断是否是回文子串

可以使用双指针法，一个指针从前向后，一个指针从后向前，如果前后指针所指向的元素是相等的，就是回文字符串了。

 bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;}

也可使用动态规划。见之后的笔记。