ST 表
ST 表,主要思想是空间换时间,用于解决可重复贡献问题和 RMQ 问题。
可重复贡献问题
指某个运算 \(op\),有 \(x\ op\ x\ =\ x\) 。例如 \(max(x,x)=x\ \ min(x,x)=x\ \ gcd(x,x)=x\)。
RMQ 问题
指在区间内的最大/最小值查询。
ST 表
ST 表基于倍增的思想,做到 \(O(n \log n)\) 的预处理时间,\(O(1)\) 的查询时间。副作用是不支持修改操作。
而 ST 表的实现类似于 dp,设 \(f_{i,j}\) 表示区间 \([i,i+2^j-1]\) 的最大值。
而显然 \(f_{i,0}=a_i\)。
为什么是 \(i+2^j-1\) 而不是 \(i+2^j\) 呢?
因为很巧,如果 \(j=0\),则 \(2^0=1\),得再减个一。
那么第二维的意思也就是在倍增的时候,调了 \(2^j-1\) 步。
那么状态转移方程:
\[f_{i,j}=max(f_{i,j-1},f_{i+2_{j-1},j-1})
\]
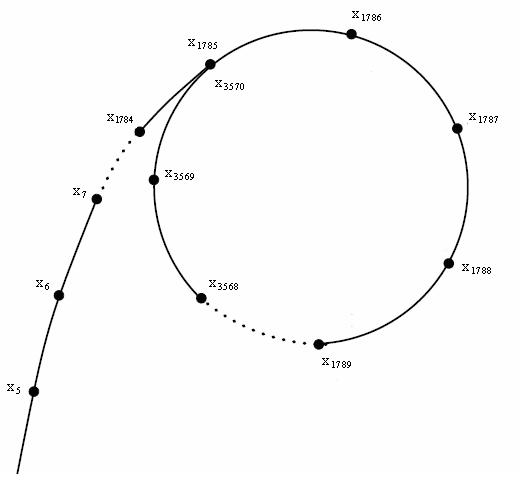
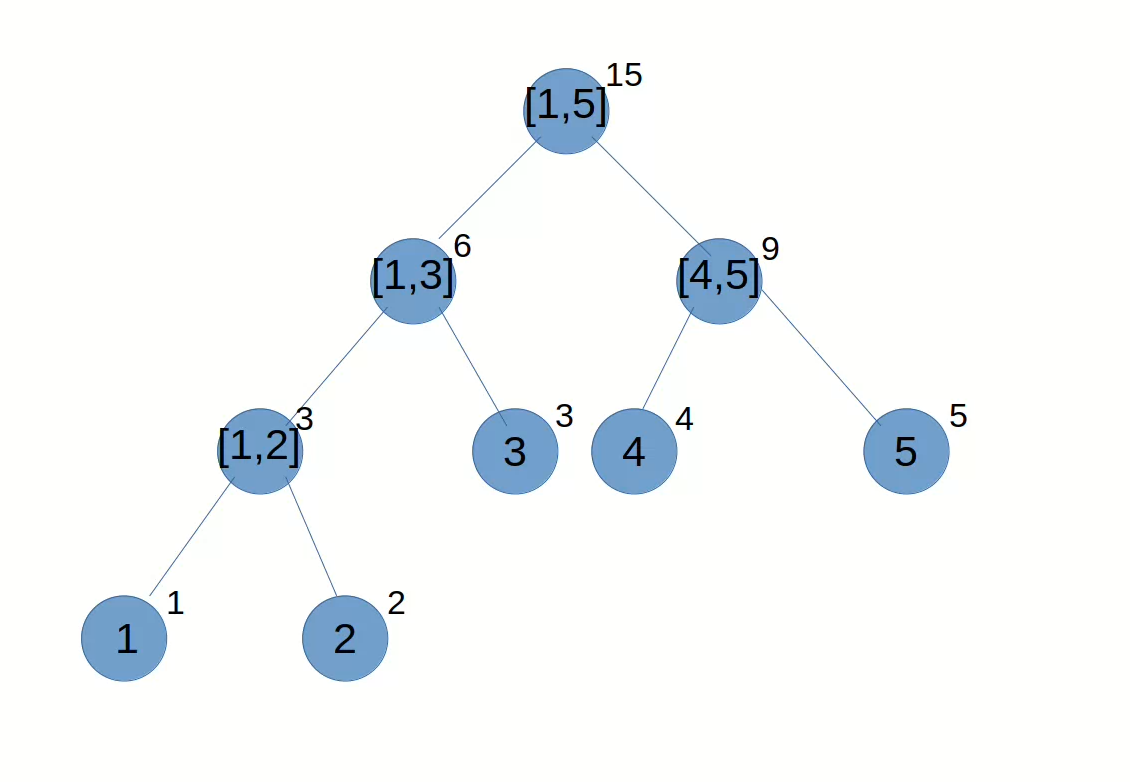
可以基于下面这张图(神图)来理解。
对于每个询问 \([l,r]\),可以分成两部分,分别是 \([l,l+2^s-1],[r-2^s+1,r]\)。
而 \(s=log_2^{r-l+1}\)。
模板代码
例题:P3865 【模板】ST 表 && RMQ 问题
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,logn=21;
int n,m,f[N][logn],Log[N],x,y,s;
inline void init()
{ Log[1]=0;Log[2]=1;for(int i=3;i<N;i++)Log[i]=Log[i/2]+1;for(int j=1;j<=logn;j++)for(int i=1;i+(1<<j)-1<=n;i++)f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);return;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++)scanf("%d",&f[i][0]);init();while(m--){scanf("%d%d",&x,&y);s=Log[y-x+1];printf("%d\n",max(f[x][s],f[y-(1<<s)+1][s]));}return 0;
}

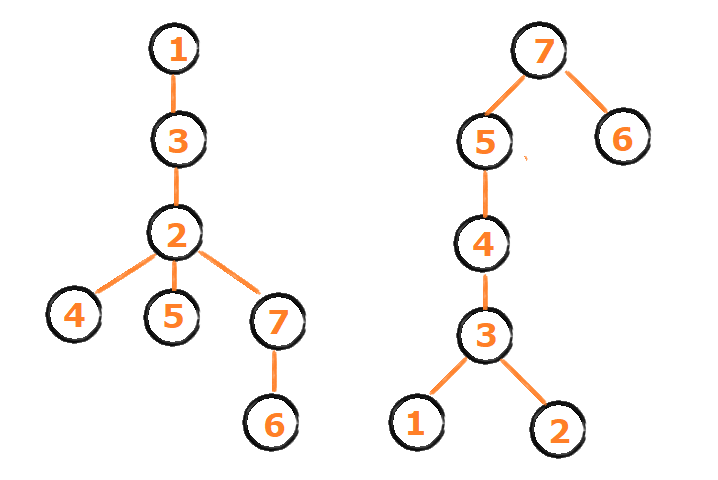
![[ARC177F] Two Airlines](https://s2.loli.net/2024/08/23/8cn96l3V7LRhGbd.png)
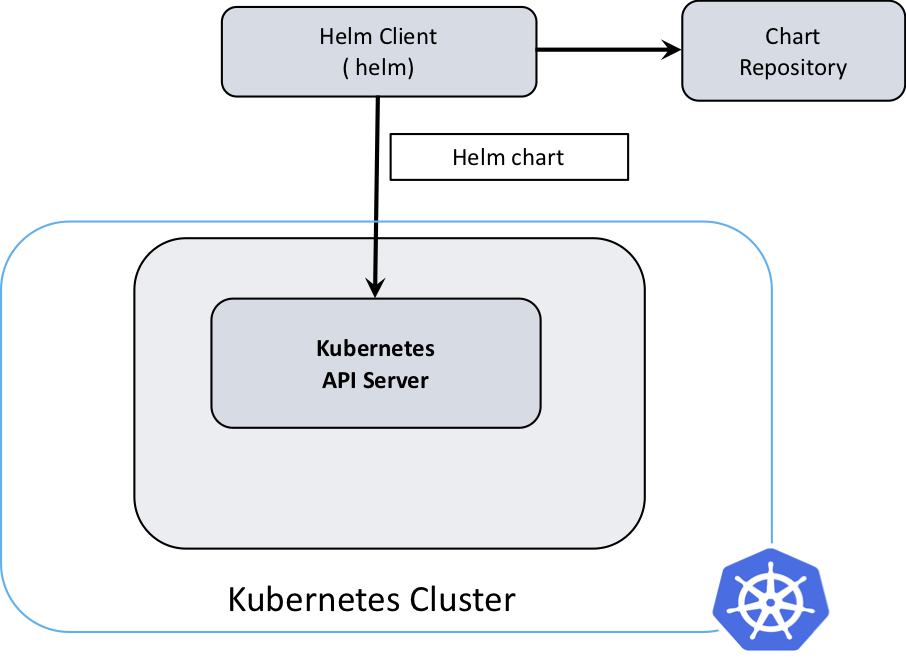
![[思考] Diffusion Model](https://img2024.cnblogs.com/blog/1067530/202403/1067530-20240314213314299-2097711653.png)