题意:给定n条线段的左右端点,求两条有公共点的线段的并的长度减去它们的交的长度最大(\(n<=2e5\) \(1<=L,R<=1e9\))
分析:不妨设\(L_i<=L_j<=R_i\),线段异或和为\(ans\),两条线段的右端点有两种情况:
1.\(R_j>=R_i\)
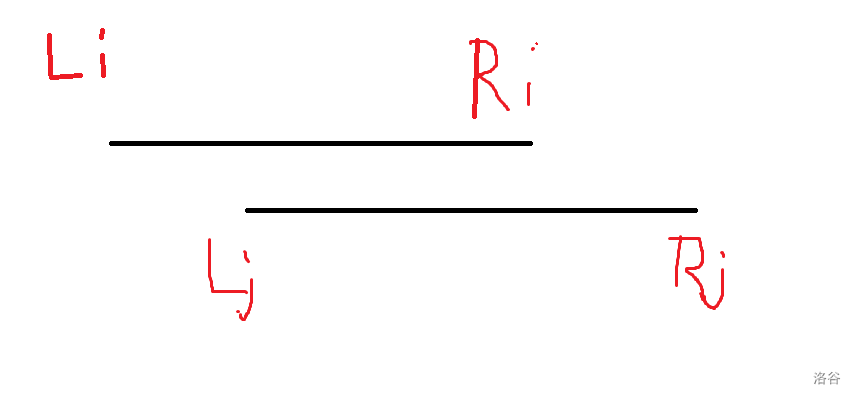
此时 \(ans=R_j-R_i+L_j-L_i=L_j+R_j-(L_i+R_i)\)
2.\(R_j<=R_i\)
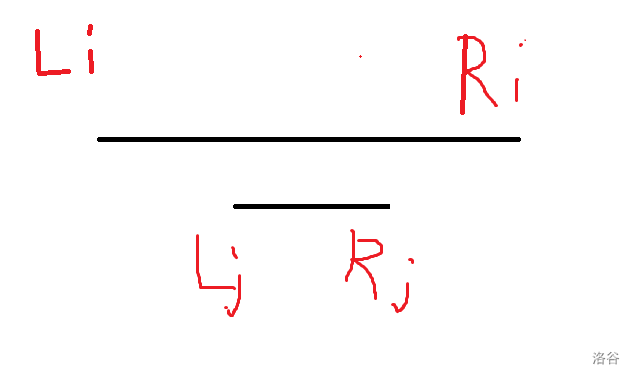
此时 $ ans=R_i-L_i-(R_j-L_j) $
按照线段的左端点从小到大排序(所以这是一个二维数点问题),对左端点相同的,按照右端点从大到小排序,对于第i条线段,每次查询\([L_i,R_i]\)内\(L+R\)的最小值(case1)和 \([R_i,n]\) 内\(R-L\)的最大值(case2),更新答案,然后在当前线段的右端点维护\(L+R\)的最小值和\(R-L\)的最大值。这个查询和修改操作可以用线段树来维护。由于端点坐标可能很大,可以预先离散化后再处理。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n,cnt;
struct line{int l,r;}d[N],g[N];
struct segtree{int l,r,len,net;}s[N<<3];
bool cmp(line c,line d){if(c.l==d.l)return c.r>d.r;return c.l<d.l;}
int h[N<<1],num;
void build(int i,int l,int r)
{s[i].l=l;s[i].r=r;if(l==r){s[i].len=h[g[l].r]-h[g[l].l]+1;s[i].net=g[l].r;return ;}int mid=(l+r)>>1;build(i<<1,l,mid);build(i<<1|1,mid+1,r);s[i].net=max(s[i<<1].net,s[i<<1|1].net);s[i].len=max(s[i<<1].len,s[i<<1|1].len);
}
void init()
{scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d%d",&d[i].l,&d[i].r);h[i]=d[i].l;h[i+n]=d[i].r;}sort(h+1,h+1+n*2);num=unique(h+1,h+1+n*2)-h-1;for(int i=1;i<=n;++i){d[i].l=lower_bound(h+1,h+1+num,d[i].l)-h;d[i].r=lower_bound(h+1,h+1+num,d[i].r)-h;}sort(d+1,d+1+n,cmp);for(int i=1;i<=n;++i){if(d[i].l!=d[i-1].l){++cnt;g[cnt].l=d[i].l;g[cnt].r=d[i].r;}}build(1,1,num);
}
int quelen(int i,int x,int y)
{if(s[i].l>=x && s[i].r<=y)return s[i].len;int mid=(s[i].l+s[i].r)>>1,sum=0;if(x<=mid)sum=max(sum,quelen(i<<1,x,y));if(y>mid)sum=max(sum,quelen(i<<1|1,x,y));return sum;
}
int quemx(int i,int x,int y)
{if(s[i].l>=x && s[i].r<=y)return s[i].net;int mid=(s[i].l+s[i].r)>>1,sum=0;if(x<=mid)sum=max(sum,quemx(i<<1,x,y));if(y>mid)sum=max(sum,quemx(i<<1|1,x,y));return sum;
}
void work()
{int ans=0;for(int i=1;i<=cnt;++i){if(g[i].r<num)ans=max(ans,h[g[i].r]-h[g[i].l]+1+quelen(1,g[i].r+1,num));ans=h[quemx(1,g[i].l,g[i].r)]-h[g[i].l]+1;}cout<<ans;
}
int main()
{init();work();return 0;
}