然后我CF上绿了
————DaisySunchaser
要多思考。
构造——从哪里入手?

CF交互指南要多注意。
我的最初想法:
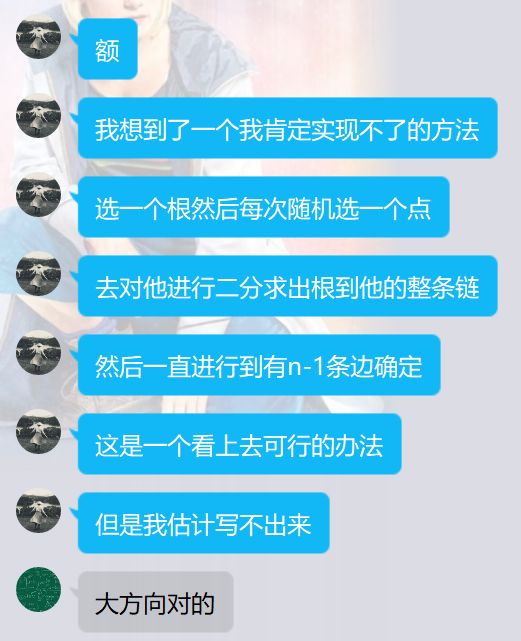
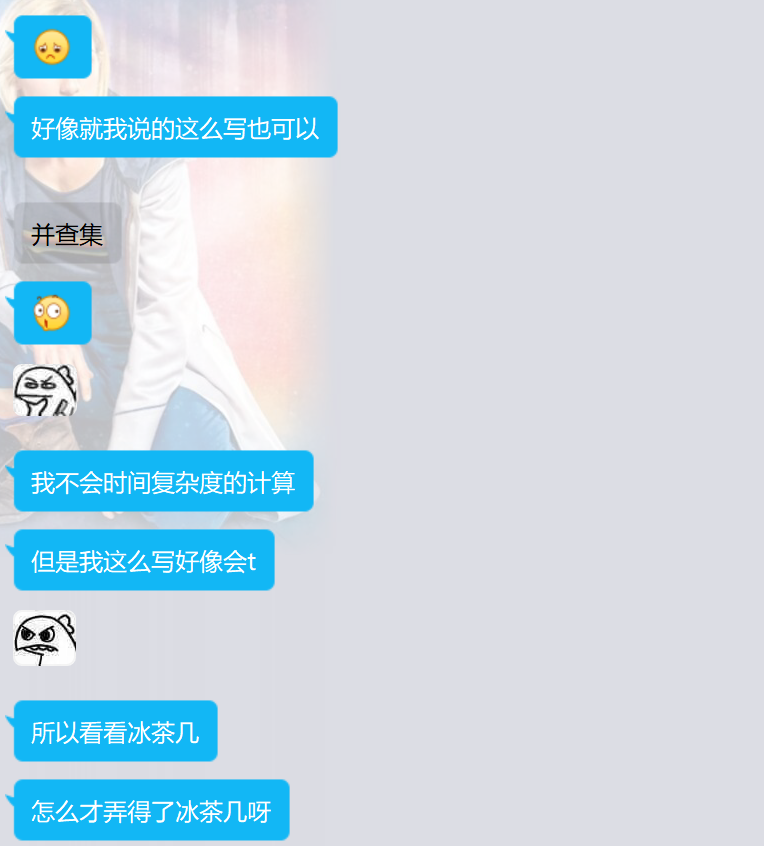
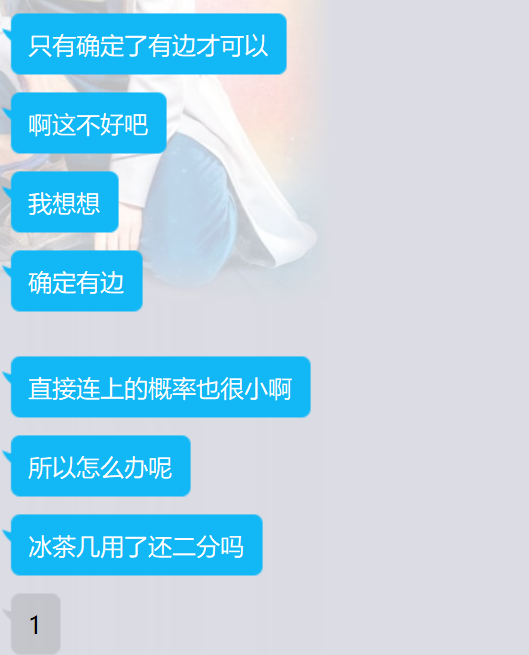

当我查看了他使用了冰茶几的代码:
#include<bits/stdc++.h>
#define ll long long
#define N 200005
#define mp make_pair
using namespace std;
int T,n,u[N],v[N],cnt,f[N];
int read()
{int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}return x*f;
}
int find(int k)
{if(f[k]==k)return k;return f[k]=find(f[k]);
}
void merge(int a,int b)
{int s1=find(a),s2=find(b);f[s1]=s2;
}
void ask(int a,int b)
{printf("? %d %d\n",a,b);fflush(stdout);
}
int check(int a,int b)
{int s1=find(a),s2=find(b);if(s1==s2) return 1;else return 0;
}
void solve(int a,int b)
{if(a==b||cnt==n-1) return;if(a>b) swap(a,b);if(check(a,b)) return;ask(a,b);int x=read();if(x==a) {merge(a,b);u[++cnt]=a;v[cnt]=b;return;}if(cnt==n-1) return;solve(a,x);if(cnt==n-1) return;solve(b,x);
}
int main()
{srand(time(0));T=read();while(T--){ n=read();cnt=0;for(int i=1;i<=n;i++) f[i]=i;for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){solve(i,j);if(cnt==n-1) break;}if(cnt==n-1) break;}printf("! ");for(int i=1;i<=n-1;i++) printf("%d %d ",u[i],v[i]);printf("\n");fflush(stdout);}return 0;
}我的想法:
如果两个点在同一个集合中,那么他们之间一定不会有边。
算是剪枝+记忆化了。
这个做法,好不好呢?当然好!对不对呢?当然对!是不是唯一做法呢?当然不是!
相信每一个题的多解性和复杂性,可尝试性.....
我想了很久,想出了一个很模糊的概念——“无解性”。
构造,交互.....这个题的前卫性也充分体现了其无解性。
每个问题,无论多难无论多易,都具有误无解性。这是很高深的概念,需要深刻地认识到信息学的本质。为了厚积薄发,我在这里就不解释了。
我想出那样的遍历方式是为了更有章法一些。如果是像他这样,当然,从头到尾地遍历也是很好的。你不用去想什么你随机问两个,虽然都差不多。
像一个迷宫,有很多的岔路,不知道最后有路可以通向终点的是哪一条岔路。
但无论选了哪一条,都要仔细地寻找接下来的出路。
CFD你要用数据结构去维护啊喂
先说这个,D哈,我思路是没问题的.......

就是暴力维护了。

要长脑子。最近有进步了啊!
求最值与判定的转换——二分答案(或之类)
先说这不是我第一次学习二分答案你这个煞笔
那么我为什么要这么说呢?
这是因为我最近看了P9755 [CSP-S 2023] 种树这个使人为之保龄的题目。
这个题真正的核心是
一棵树,一时刻遍历一个点,必须从已遍历的点过去,第$i$个点需要在第$a_i$时刻以前遍历,问$t$时刻能否按规定完成全树遍历
这恐怕是一个很common的idea吧!难以想象以前居然没有人把这个出成题
说到这个怎么做乍一看想不出来,其实也很简单,就按时间限制把所有节点从小到大排序,然后从前往后依次过去即可,如果已经被访问的就跳过,很易证的贪心。
其实像这样的容易想到的idea有很多,网上也有流传一些集锦。
所以,我亲爱的同学,如果你问如何出一道好题
- 随便找一个好找但是又不是特别普遍的idea
- 使用一些数学之类的技巧对idea进行包装并在处理上增加难度
- 如果最后是判定,再来一个二分答案将其转化成求最值——完美的好题。
逆向思维——玄而精妙
来看经典题P3243 [HNOI2015] 菜肴制作
我自以为是的提交记录:

实际上,我们的脑子无比地混乱。欲图真正地想出一个题的正解,何其不易。
这个题,既不是DFS,也不是局部拓扑排序,更不是很多人以为的简单拓扑排序,而是逆向拓扑序。
虽然建了反图,但我着实没有想到这个。前面我的思路还要不少的数据对他进行hack才可以知道哪里错了,但看了正解,几乎是一目了然。
题解有很多是错误和意表不清的,但这里可以借用一个题解图:

按照题意,我们应当先搞2再搞3。但是如果是求字典序最小的拓扑序,就会先考虑先入的(5或4),而后入的2或3就算3在前面,对他来说也是ok的,因为后面的位贡献没有前面的位大。这是很普遍的关于高位与地位贡献的贪心。
但是我们的题意不是这么要求的。后面2和3的贡献应当大于前面5或4的贡献。这应该怎么办呢?
倒过来呗。
反过来依然满足简单的关于位与贡献的贪心。把题意也符合了。
至于反过来求拓扑并从大到小,最后倒过来输出的这个事情吧,你看到虽然是没问题的,其实不好想。
一般来说,我们看到拓扑,都没有想过他可以倒过来......而且反图、从大到小、倒序输出这些也是比较复杂的工序。
其实关于这个,第一篇题解就说的比较好(但是单看第一篇题解可能理解不了)(后面的题解也没有好到哪里去)

其实对于任何一个看似有着单向矛盾的问题,想办法逆过来,也许可以解决。就像动脉血管的瓣膜一样,当血液正向流动时非常顺畅,但如果要逆流就会受到阻碍(自以为很形象的比喻)
我思考了很久,最终想到了一个不再模糊的概念——“可逆化”。
任何事物都存在某种层面上的可逆化。对于某些来说,寻找他的可逆是很简单、很漫长的过程,是十分艰难的。但谁知道呢?也许找到了血管的正方向,问题就会迎刃而解。
对于这个问题来说,如果贡献更大的在后面,而要求的又是前大后小贡献的,那么简单的反过来就是了。
当然很多问题不是这么简单的。也许会有许多方向不同的瓣膜,只能去使用类似搜索的方式去真正地寻找。
只是提供一个很珍贵的思路罢了。
最后关于对拍:
如果你要拍的是n<=10~20的,最好拍到10000组以上。
#include<cstdlib>
#include<cstdio>
#include<ctime>
int main(){for(int T=1;T<=10000;T++){system("random.exe");double st=clock();system("bf.exe");double ed=clock();system("sol.exe");if(system("fc out.txt ans.txt")){puts("Wrong Answer");return 0;}else{printf("Accepted,测试点 #%d,用时 %.0lfms\n",T,ed-st);}}
}以及单独建的一个文件夹、对每个问题单独存储的子文件夹。
学会对拍,很多好处!(比如在凡人面前装逼)
随机化——什么奇奇怪怪奇技淫巧
一直想去学模拟退火来着
在我非常不成熟的时候,对算法有着四种分类:
- “暴力”类:通过直接遍历状态空间来找到答案。
- “贪心”类:指问题本身有着某种性质、满足某种逻辑关系,并可以利用这种关系来优化暴力去解题。
- “DP”类:通过充分利用已遍历状态空间、避免重复遍历空间来优化暴力。
- “随机”类:顾名思义,是通过随机化与概率论来实现的。
这四类可能被认为是四大“基本元素”。他们一般不会单独出现,而是以复合的形式。现在来看,一个是觉得不成熟,一个是觉得不完全。不过她已经做得很好了。
我认为前三个可以分成一大类,第四个则自成一派。因为这是两种完全不同的做法——在前三个的认识中,一个问题的状态空间始终在那里,你无论怎么做都无法在不访问完他的情况下求出答案,你能做的只有优化。而第四个则可以通过随机对状态空间进行选择性访问,最后再利用其概率大小来估算正确的可能性。在前三个的下面,“暴力”类和“DP”类又可以归成一小类(通过优化或不优化遍历整个状态空间),“贪心”类的做法则相对独立(利用性质对状态空间本身进行优化)。
“随机化”作为一个遗世而独立的类,一直吸引着我的兴趣。
这天,我看了这个年轻的我用Floyd和DFS写了60分的题P8817 [CSP-S 2022] 假期计划
因为看不懂正解,偶然翻到了一篇indie tj:

我思考良久,终于.....
他这样做,也就把原问题弱化成了:每个点都有编号1234,第一个点只能是编号为1的,第二个点只能是编号为2的.....这样,我就会做了呀!
而$\frac{2}{4^4}$则是因为,答案的那四个点的排列顺序1,2,3,4,每个点有$\frac{1}{4}$的概率随机到正确的编号,一共是$\frac{1}{4} * \frac{1}{4} * \frac{1}{4} * \frac{1}{4} = \frac{1}{4^4}$,加上四个点的顺序正着、反着都是一样的,所以一共是$\frac{2}{4^4}$。
不过随机化,当然是随机地越多,对的可能性也越大。我们应当在不T的情况下尽可能地多去随机。这就需要用到卡时。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mxn=2505;
vector<int>g[mxn],ng[mxn];
ll n,m,k;
ll a[mxn];
int dist[mxn][mxn];
inline void bfs(int x){queue<int>q;for(;q.size();)q.pop();q.push(x);memset(dist[x],63,sizeof(dist[x]));dist[x][x]=0;for(;q.size();){int u=q.front();q.pop();for(int v:g[u])if(dist[x][v]>dist[x][u]+1){dist[x][v]=dist[x][u]+1;q.push(v);}}
}
int col[mxn];
ll dp[mxn],ans;
inline ll dfs(int x,int d){if(dp[x]!=-1)return dp[x];dp[x]=-5000000000000000000ll;if(d==4){if(dist[1][x]<=k+1)dp[x]=a[x];else dp[x]=-5000000000000000000ll;return dp[x];}for(int y:ng[x])if(col[y]==d+1)dp[x]=max(dp[x],dfs(y,d+1)+a[x]);return dp[x];
}
int main(){clock_t st=clock();ios_base::sync_with_stdio(false);srand(1919810);cin>>n>>m>>k;for(int i=2;i<=n;++i)cin>>a[i];for(int i=1,u,v;i<=m;++i){cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}for(int i=1;i<=n;++i)bfs(i);for(int i=1;i<=n;++i)for(int j=i+1;j<=n;++j)if(dist[i][j]<=k+1){ng[i].push_back(j);ng[j].push_back(i);}for(int ee=0;ee<10000;++ee){if(clock()-st>1.98*CLOCKS_PER_SEC)break;if(rand()%3==1)rand();for(int i=2;i<=n;++i)col[i]=rand()%4+1;memset(dp,-1,sizeof(dp));dfs(1,0);ans=max(ans,dp[1]);}cout<<ans<<endl;return 0;
}如代码所示,也像对拍一样,我们在程序开始时使用clock()记录下现在的时间;并在每一次将要再次进行随机时判断现在是否超过1980ms(时限2s,CLOCKS_PER_SEC=1000,表示1s内CPU运行的时钟周期数为1000个,相当于1ms一个时钟周期,因此一般说操作系统的单位是毫秒)。这样,我们就最大限度地进行了随机化。
在实测中,若修改为1990ms则有一个点TLE;若直接上1s居然全都过了
由此可见,随机化+卡时是一个相当好的算法(主要是我非常喜欢)。
所以综上来说,遇到一个问题,我们一定要敢于去思考吧。设想一种问题的子情况,如果这种情况可以推到全局,那当然是好的;如果没有办法了,我们也可以通过随机化,把全局都变成这种情况,再来计算概率、卡时。
以上都只是一些小小的技巧。真正的实践过程中,当然可以想着如何套用,但更多地需要随机应变、灵活操作。