My Blogs
[ARC183D] Keep Perfectly Matched
这场不打感觉亏麻了,怎么大家都不会 D。首先匹配路径长度之和最大,很典的想到取重心,猜测答案上界 \(\sum_i dep_i\) 可以取到。
取完重心之后,希望不断把两个不同的子树里的点进行匹配,直到删空。因为原树本身存在完美匹配,所以找一对不同子树里的点删去后,根节点的匹配一定变了。
所以选的点一定有一个在根节点当前的匹配点的子树里,否则根节点没有理由更改匹配点。设这个点为 \(x\),则 \(x\) 一定满足:其到根的路径上,边的种类是“匹配边,非匹配边,匹配边...”,即:
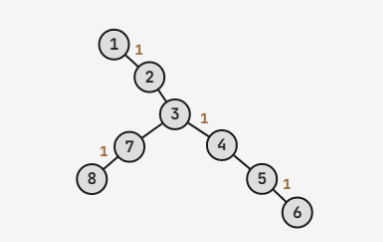
图中标 \(1\) 的边是匹配边,可以发现删六号点是合法的,而删 \(8\) 号点的过程中会因为连续出现了两条非匹配边而寄掉。
这样确定了一个子树中的点,另一个点是可以任意选的。因为要尽量匹配对,所以另一个点应该选在除此之外的 \(siz\) 最大的子树里面。接下来根的匹配就是选的第二个子树中的根节点。继续做上述过程即可。
这样做为何能取到最优值:设 \(x\) 是根的初始匹配节点,首先第一次删点的两棵子树一定分别是 \((x,y)\),然后第二次因为此时根和 \(y\) 匹配,所以要删 \((y,z)\),以此类推,可以发现除了开始的 \(x\) 删了一个点,剩下的操作都是,选一个子树删两个点,然后跳到另一棵子树。
除了 \(x\) 子树大小是奇数,剩下的子树大小都是偶数,一开始 \(x\) 删了 \(1\) 就全部变成了偶数。所以不会有奇偶性不对的情况。如果跳到另一棵子树选择当前 \(siz\) 最大的,那就一定能够删空。因为此时根是树的重心,每个子树内需要的操作次数大小都不会超过 \(\frac m 2\),其中 \(m\) 是总操作次数,所以这样做一定不会爆掉。
现在的问题就是如何高效的找出当前能删掉的合法点。策略也很简单:对于点 \(x\) 来说,如果初始他的匹配是他的父亲,则他儿子可以按任意顺序一个一个删光。
如果初始他的匹配是他的某个儿子,则先把这个儿子全部删空时最优的。然后他的匹配就变成了他的父亲,他剩下的儿子可以任意排列。
可以 \(\text{dfs}\) 求出每个子树的后序遍历,如果有某个儿子和他匹配就优先向这个儿子走,这样可以求出每个点的合法操作序列。然后套用上述过程,总复杂度 \(\mathcal O(n\log n)\) 或者 \(\mathcal O(n)\)。
int n,rt,minn=inf,len,ans[500010],siz[250010];
vi T[250010],ve[250010];
void findrt(int x,int fa=0)
{int maxn=0;siz[x]=1;for(auto to:T[x])if(to!=fa)findrt(to,x),siz[x]+=siz[to],Mmax(maxn,siz[to]);if(Mmin(minn,max(n-siz[x],maxn)))rt=x;
}
void dfs(int x,int fa,int top)
{ve[top].eb(x);for(auto to:T[x])if(to!=fa&&to!=(((x-1)^1)+1))dfs(to,x,top);if(fa!=(((x-1)^1)+1))dfs(((x-1)^1)+1,x,top);
}
priority_queue<pii> q;
inline void mian()
{read(n);int x,y;pii p;for(int i=1;i<n;++i)read(x,y),T[x].eb(y),T[y].eb(x);findrt(1),findrt(rt);for(auto to:T[rt])dfs(to,rt,to);int pos=((rt-1)^1)+1;ans[++len]=ve[pos].back(),ve[pos].pop_back(),--siz[pos];for(auto to:T[rt])q.e(mp(siz[to],to));for(int I=1;I<(n>>1);++I){if(q.top().se==pos)p=q.top(),q.pop();else p=mp(-1,-1);pos=q.top().se;ans[++len]=ve[pos].back(),ve[pos].pop_back();ans[++len]=ve[pos].back(),ve[pos].pop_back();siz[pos]-=2;q.pop(),q.e(mp(siz[pos],pos));if(p.fi!=-1)q.e(p);}for(auto to:T[rt])if(siz[to])ans[++len]=to;ans[++len]=rt;for(int i=1;i<=len;i+=2)write(ans[i],' ',ans[i+1],'\n');
}