OK,老规矩,先复习一下昨天的内容
.....
几分钟就复习了,直接开干今天的内容
先找大佬的wp
来源:
TEA系列加密解密 | Gruge's Blog (g2uge.github.io)
逆向算法之TEA算法 - Sk2rw - 博客园 (cnblogs.com)
一.TEA加密解密简介
在密码学中,微型加密算法(Tiny Encryption Algorithm,TEA)是一种易于描述和执行的块密码,通常只需要很少的代码就可实现。
代码的特点:
- 加密使用的数据为2个32位无符号整数,密钥为4个32位无符号整数即密钥长度为128位(当加密解密的对象是一串数组的时候,需要将这个32位无符号整数的数组每两个32位无符号整数划分为一组,对每一组数据单独加密解密得到结果)
- 该算法使用了一个常数 δ 作为倍数,它来源于黄金比率,以保证每一轮加密都不相同。但 δ 的精确值似乎并不重要,这里 TEA 把它定义为 δ=「(√5 - 1)231」(也就是程序中的 0×9E3779B9)作为魔数(了解即可)
加密过程
拥有一个叫做Feistel 结构的密码学结构。这种密码学结构通俗的来讲就是会将加密的plaintext分成L、R两部分,并且满足 L_{i+1} = R_i, R_{i+1} = F(K_i,R_i) \oplus L_i 这种交换式的加密方式的一种结构。
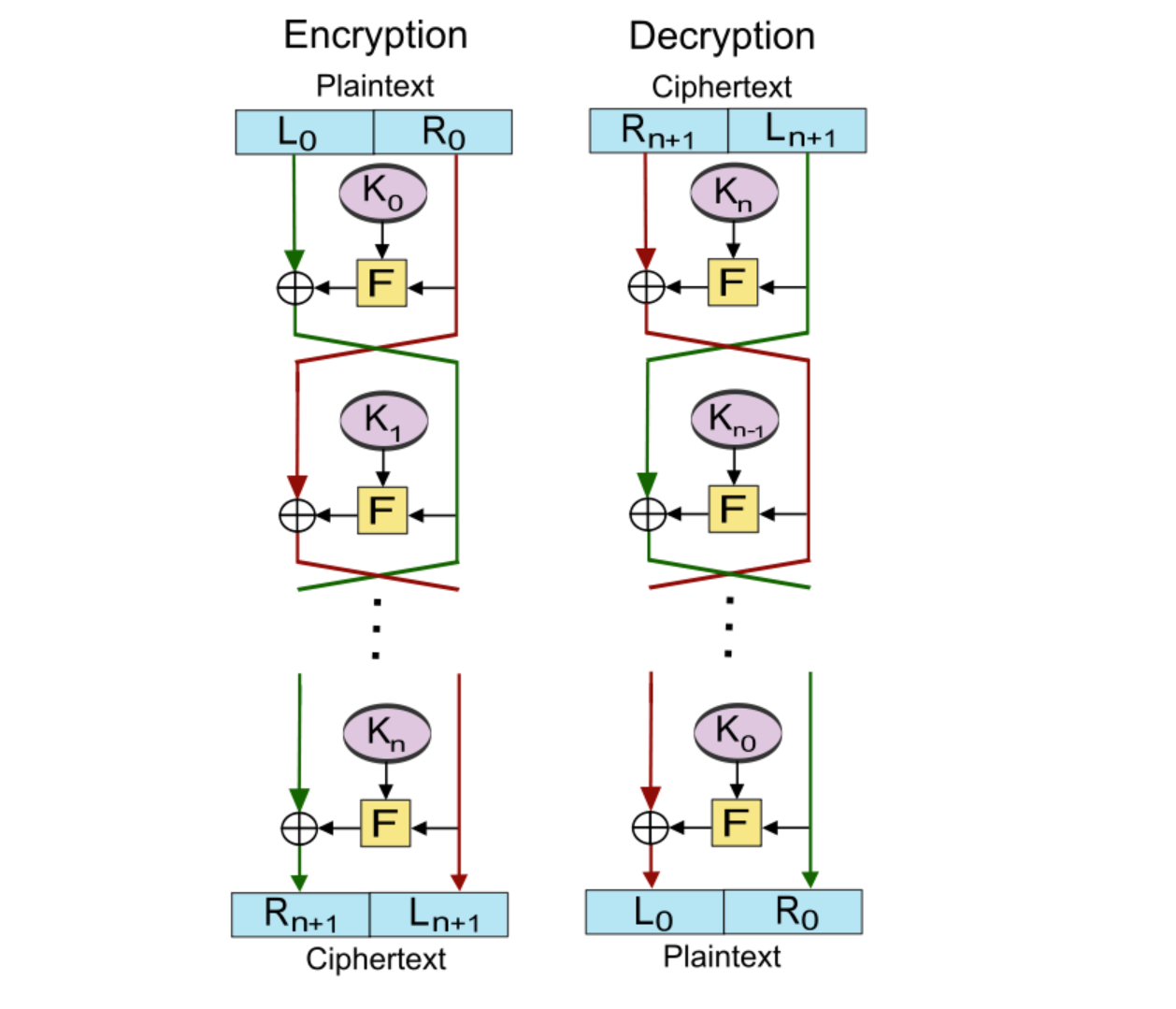
TEA加密算法的实现
参数要求:输入一定要是一个64bit的数字,或者可以写作一个拥有两个元素的32bit的数组。并且需要一个两倍长度的key(int[4]),即一个128位的数字(拥有四个元素的32bit的数组)
加密特征:存在一个delta值,这个值会不停的增加到sum之中,形成一种循环的效果;会有一个位移->与密钥相加->异或的过程;
计算delta的sum状态值也会参与
void encrypt (uint32_t v[2], const uint32_t k[4]) {uint32_t v0=v[0], v1=v[1], sum=0, i; /* set up */uint32_t delta=0x9E3779B9; /* a key schedule constant */uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */for (i=0; i<32; i++) { /* basic cycle start */sum += delta;v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);} /* end cycle */v[0]=v0; v[1]=v1;
}
代码解释(v1<<4)--->将v1的进制左移两位
用11001100举例解释
好的,我们将使用二进制数 11001100 作为例子来解释左移操作。这个二进制数是一个8位的数,其十进制值为204(如果你计算的话:1*2^7 + 1*2^6 + 0*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 0*2^0 = 128 + 64 + 0 + 0 + 8 + 4 + 0 + 0 = 204)。
原始二进制数
原始二进制数 x:
11001100
左移2位操作
现在,我们要将这个数向左移动2位。左移操作意味着我们将所有位都向左移动指定的位数(在这个例子中是2位),并且在右侧新增相应数量的0来填补空位。最左边的位(在这个例子中是 11)将会超出边界并被丢弃。
左移2位后的结果:
(被丢弃的位) |--|-- v v
11|00110000| (同样,这里的空格是为了对齐,实际中并不存在)
去掉被丢弃的位和额外的空格后,我们得到:
100110000
但是,这里有一个问题:我们原始的二进制数是一个8位的数。当我们左移2位后,它实际上变成了一个9位的数。然而,在大多数计算机系统中,如果我们有一个8位的变量,并且我们尝试将一个9位的数存储到它里面,那么最高位(在这个例子中是最左边的 1)将会被丢弃,以符合8位的限制。
因此,如果我们是在一个8位的上下文中进行这个操作(比如,在一个8位的寄存器或变量中),那么结果应该是这样的:
00110000
这个二进制数转换为十进制是 48(0*2^7 + 0*2^6 + 1*2^5 + 1*2^4 + 0*2^3 + 0*2^2 + 0*2^1 + 0*2^0 = 0 + 0 + 32 + 16 + 0 + 0 + 0 + 0 = 48)。
结论
所以,当我们将二进制数 11001100 向左移动2位时,并且假设我们是在一个8位的上下文中进行这个操作,我们得到的结果是 00110000(十进制中的48)。这个操作相当于将原始的十进制数204除以4(因为我们是左移2位,相当于乘以2的-2次方,即除以4),并取结果的低8位(在这个例子中,结果本身就没有超过8位,所以直接就是48)。
TEA解密算法的实现
参数要求:输入一定要是一个64bit的数字,或者可以写作一个拥有两个元素的32bit的数组。并且需要一个两倍长度的key(int[4]),即一个128位的数字(拥有四个元素的32bit的数组)
//解密函数
void decrypt (uint32_t* v, uint32_t* k) { uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up */ uint32_t delta=0x9e3779b9; /* a key schedule constant */ uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */ sum = delta << 5; //32轮运算,所以是2的5次方;16轮运算,所以是2的4次方;8轮运算,所以是2的3次方for (i=0; i<32; i++) { /* basic cycle start */ v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3); v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1); sum -= delta; } /* end cycle */ v[0]=v0; v[1]=v1;
}
可能你和我一样,有点不太懂,但是这不是你放弃的理由,慢慢了解
我的理解就是加密就是一个算法,解密也就是逆过来,
k0与k2互换,v0与v1换,左移变成右移
TEA补充脚本
def encrypt(v, k):v0 = v[0]v1 = v[1]x = 0delta = 0x9E3779B9k0 = k[0]k1 = k[1]k2 = k[2]k3 = k[3]for i in range(32):x += deltax = x & 0xFFFFFFFFv0 += ((v1 << 4) + k0) ^ (v1 + x) ^ ((v1 >> 5) + k1)v0 = v0 & 0xFFFFFFFFv1 += ((v0 << 4) + k2) ^ (v0 + x) ^ ((v0 >> 5) + k3)v1 = v1 & 0xFFFFFFFFv[0] = v0v[1] = v1return v
def decrypt(v, k):v0 = v[0]v1 = v[1]x = 0xC6EF3720delta = 0x9E3779B9k0 = k[0]k1 = k[1]k2 = k[2]k3 = k[3]for i in range(32):v1 -= ((v0 << 4) + k2) ^ (v0 + x) ^ ((v0 >> 5) + k3)v1 = v1 & 0xFFFFFFFFv0 -= ((v1 << 4) + k0) ^ (v1 + x) ^ ((v1 >> 5) + k1)v0 = v0 & 0xFFFFFFFFx -= deltax = x & 0xFFFFFFFFv[0] = v0v[1] = v1return v
if __name__ == '__main__':plain = [1, 2]key = [2, 2, 3, 4]encrypted = encrypt(plain, key)print(encrypted)decrypted = decrypt(encrypted, key)print(decrypted)
"""
[1347371722, 925494771]
[1, 2]"""
实例
解密数组:{0x3e8947cb,0xcc944639,0x31358388,0x3b0b6893,0xda627361,0x3b2e6427}
key数组:{0x4445,0x4144,0x4245,0x4546}
因为在解密的过程之中会产生移位的运算,这个过程会产生溢出,所以每组解密的对象声明成 v1[3]={0x3e8947cb,0xcc944639,0x0} 这样的形式
#include <stdio.h>
#include <stdint.h>
void decrypt (uint32_t* v, uint32_t* k) {uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i; /* set up */uint32_t delta=0x9e3779b9; /* a key schedule constant */uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3]; /* cache key */for (i=0; i<32; i++) { /* basic cycle start */v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);sum -= delta;} /* end cycle */v[0]=v0; v[1]=v1;
}int main()
{uint32_t v1[3]={0x3e8947cb,0xcc944639,0x0},k[4]={0x4445,0x4144,0x4245,0x4546};uint32_t v2[3]={0x31358388,0x3b0b6893,0x0};uint32_t v3[3]={0xda627361,0x3b2e6427};decrypt(v1, k);decrypt(v2, k);decrypt(v3, k);printf("解密后的数据:%s %s %s\n",(char*)v1,(char*)v2,(char*)v3); // 注意如何将一串数组以字符串的形式输出return 0;
}
//输出的结果:fvBXQdEa rcbvhBPx cOA8Ag6J
遇到新知识,学一下
代码解释_元组
元组(Tuple)是Python中的一种内置数据结构,用于存储一系列不可变(immutable)的元素。与列表(List)不同,元组一旦被创建,其内部的元素就不能被修改(即不能添加、删除或更改元素)。元组通常用于存储那些不应该被改变的数据集合,比如数据库查询的结果、函数的多个返回值等。
元组使用圆括号()来定义,元素之间用逗号,分隔。如果元组中只有一个元素,那么需要在该元素后面加上逗号,,以区分该元素和圆括号本身(后者在Python中通常用于分组或调用函数)。
示例
- 定义一个简单的元组:
my_tuple = (1, 2, 3, 4, 5)
- 定义一个只包含一个元素的元组(注意逗号):
single_element_tuple = (1,)
- 访问元组中的元素:
元组中的元素可以通过索引来访问,索引从0开始。
print(my_tuple[0]) # 输出: 1
print(my_tuple[-1]) # 输出: 5,使用负索引访问最后一个元素
- 元组是不可变的:
尝试修改元组中的元素会引发TypeError。
# 尝试修改元组中的元素
my_tuple[0] = 10 # TypeError: 'tuple' object does not support item assignment
- 元组的应用场景:
- 作为字典的键(因为字典的键需要是不可变的)。
- 存储函数的多个返回值(Python允许函数返回多个值,实际上是以元组的形式返回的)。
- 在需要不可变序列的场合,比如作为集合(Set)的元素或另一个元组的元素。
元组由于其不可变性,在某些情况下比列表更加高效,因为Python解释器可以对它们进行更多的优化。然而,这也意味着在某些需要频繁修改数据的场合,使用列表可能更为合适。
我的理解就是用括号括起来的数组
二.XTEA加密解密
XTEA是TEA的升级版,增加了更多的密钥表,移位和异或操作
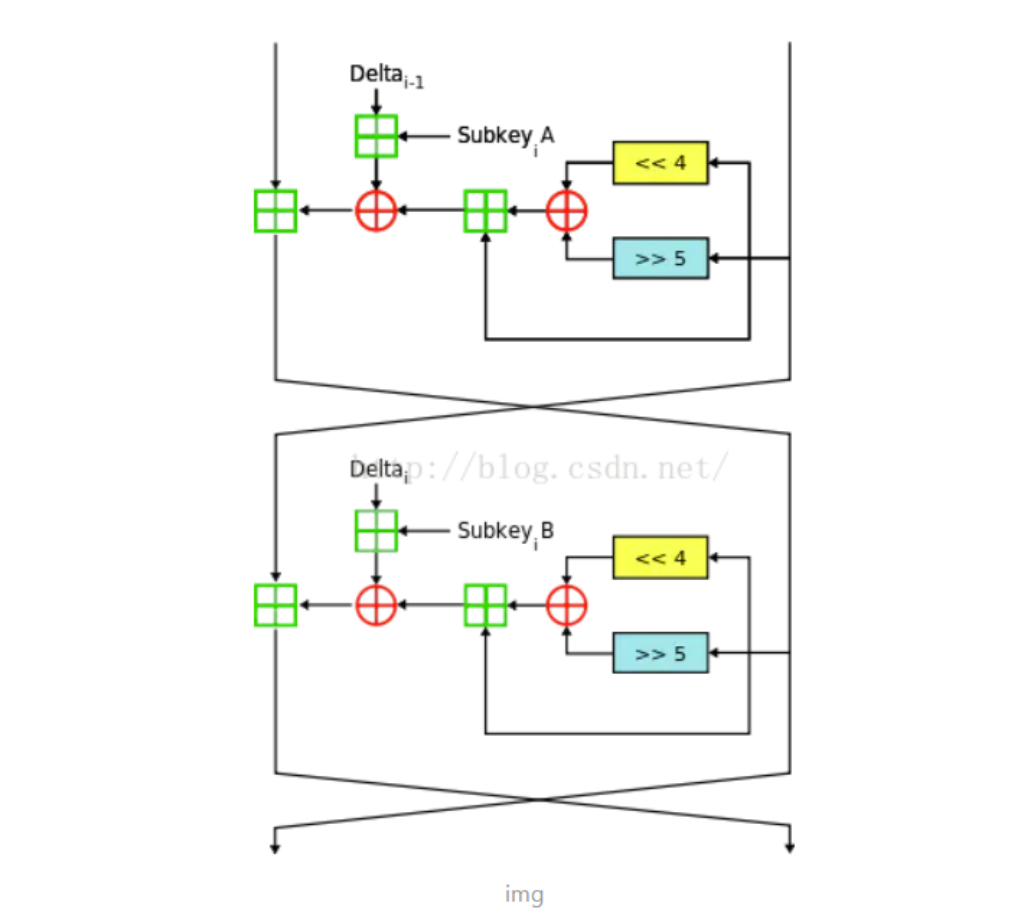
XTEA加密算法的实现
相较于TEA的变化:
- 由之前的
((v1<<4) + k0) ^ ((v1>>5) + k1)变化成了((v1 << 4) ^ (v1 >> 5)) + v1),此时v1内部数据的加密变化不再受到密钥的影响。 - 原先的
v1 + sum变成了(sum + key[sum & 3])以及sum + key[(sum>>11) & 3],密钥变成了轮转使用,而不是固定只针对某种数据进行加密(解密)。并且此时密钥的选取受到sum的影响 sum += delta的时机由每次加密开头就发生变化到v0,v1两个block加密的中间。
输入的参数:输入一定要是一个64bit的数字,或者可以写作一个拥有两个元素的32bit的数组。并且需要一个两倍长度的key(int[4]),即一个128位的数字(拥有四个元素的32bit的数组),注意这里循环的次数不是固定的了,是需要传入的参数num_rounds
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) { unsigned int i; uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9; for (i=0; i < num_rounds; i++) { v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]); sum += delta; v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]); } v[0]=v0; v[1]=v1;
}
XTEA解密算法的实现
输入的参数:输入一定要是一个64bit的数字,或者可以写作一个拥有两个元素的32bit的数组。并且需要一个两倍长度的key(int[4]),即一个128位的数字(拥有四个元素的32bit的数组),注意这里循环的次数不是固定的了,是需要传入的参数num_rounds
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) { unsigned int i; uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds; for (i=0; i < num_rounds; i++) { v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]); sum -= delta; v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]); } v[0]=v0; v[1]=v1;
}
XTEA补充脚本
def encrypt(rounds, v, k):v0 = v[0]v1 = v[1]x = 0delta = 0x9E3779B9for i in range(rounds):v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (x + k[x & 3])v0 = v0 & 0xFFFFFFFFx += deltax = x & 0xFFFFFFFFv1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (x + k[(x >> 11) & 3])v1 = v1 & 0xFFFFFFFFv[0] = v0v[1] = v1return v
def decrypt(rounds, v, k):v0 = v[0]v1 = v[1]delta = 0x9E3779B9x = delta * roundsfor i in range(rounds):v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (x + k[(x >> 11) & 3])v1 = v1 & 0xFFFFFFFFx -= deltax = x & 0xFFFFFFFFv0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (x + k[x & 3])v0 = v0 & 0xFFFFFFFFv[0] = v0v[1] = v1return v
if __name__ == '__main__':plain = [1, 2]key = [2, 2, 3, 4]rounds = 32encrypted = encrypt(rounds, plain, key)print(encrypted)decrypted = decrypt(rounds, encrypted, key)print(decrypted)
"""
[1345390024, 2801624574]
[1, 2]
"""
示例代码
#include <stdio.h>
#include <stdint.h>/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {unsigned int i;uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;for (i=0; i < num_rounds; i++) {v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);sum += delta;v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);}v[0]=v0; v[1]=v1;
}void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {unsigned int i;uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;for (i=0; i < num_rounds; i++) {v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);sum -= delta;v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);}v[0]=v0; v[1]=v1;
}int main()
{uint32_t v[3]={0x73647979,0x726b6f5f,0x0};uint32_t v1[2]={0x646f675f,0x0};uint32_t const k[4]={0X95C4C,0X871D,0X1A7B7,0X12C7C7};unsigned int r=32;//num_rounds建议取值为32// v为要加密的数据是两个32位无符号整数// k为加密解密密钥,为4个32位无符号整数,即密钥长度为128位printf("加密前原始数据:%s%s\n",(char*)v,(char*)v1);encipher(r, v, k);encipher(r, v1, k);printf("加密后的数据:%u %u %u\n",v[0],v[1],v1[0]);decipher(r, v, k);decipher(r, v1, k);printf("解密后的数据:%s%s\n",(char*)v,(char*)v1);return 0;
}
/*
结果:
加密前原始数据:yyds_okr_god
加密后的数据:3461349474 1314311102 3609197830
解密后的数据:yyds_okr_god
*/
三.XXTEA加密解密
介绍
XTEA再度进化, 变成了支持块加密XXTEA
加密过程
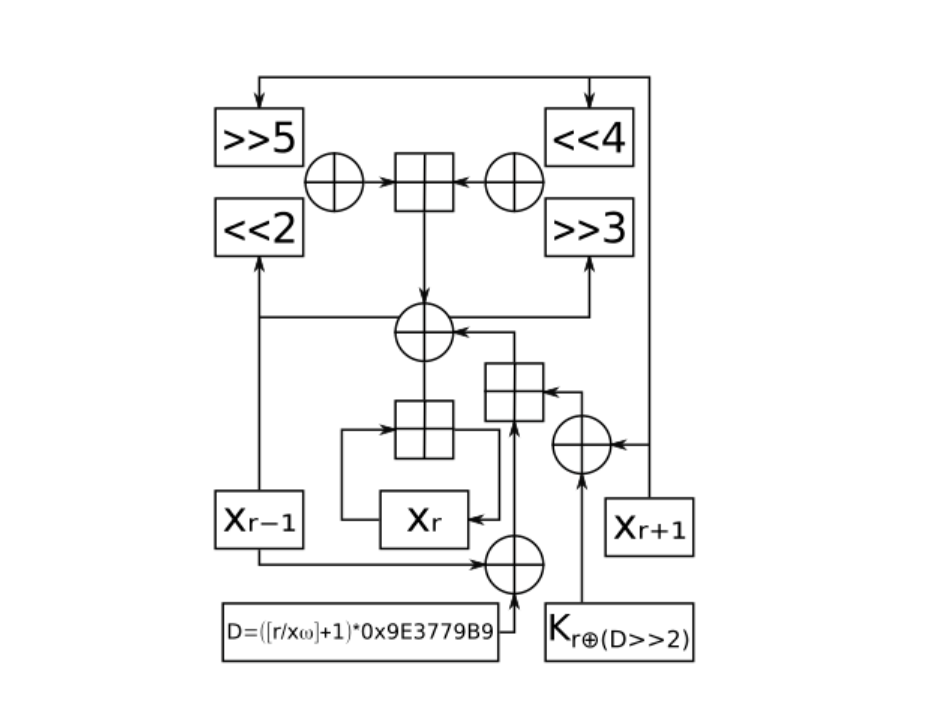
XXTEA加密解密算法的实现
特点:在可变长度块上运行,这些块是32位大小的任意倍数(最小64位),使用128位密钥, 是目前TEA系列中最安全的算法,但性能较上两种有所降低。
参数:输入的是至少拥有两个元素的32bit的数组,密钥的长度仍然是128位,即拥有4个元素32位长度的数组
#include <stdio.h>
#include <stdint.h>
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z))) void btea(uint32_t *v, int n, uint32_t const key[4])
{ uint32_t y, z, sum; unsigned p, rounds, e; if (n > 1) /* Coding Part */ { rounds = 6 + 52/n; sum = 0; z = v[n-1]; do { sum += DELTA; e = (sum >> 2) & 3; for (p=0; p<n-1; p++) { y = v[p+1]; z = v[p] += MX; } y = v[0]; z = v[n-1] += MX; } while (--rounds); } else if (n < -1) /* Decoding Part */ { n = -n; rounds = 6 + 52/n; sum = rounds*DELTA; y = v[0]; do { e = (sum >> 2) & 3; for (p=n-1; p>0; p--) { z = v[p-1]; y = v[p] -= MX; } z = v[n-1]; y = v[0] -= MX; sum -= DELTA; } while (--rounds); }
}
XXTEA补充脚本:
def shift(z, y, x, k, p, e):return ((((z >> 5) ^ (y << 2)) + ((y >> 3) ^ (z << 4))) ^ ((x ^ y) + (k[(p & 3) ^ e] ^ z)))
def encrypt(v, k):delta = 0x9E3779B9n = len(v)rounds = 6 + 52 // nx = 0z = v[n - 1]for i in range(rounds):x = (x + delta) & 0xFFFFFFFFe = (x >> 2) & 3for p in range(n - 1):y = v[p + 1]v[p] = (v[p] + shift(z, y, x, k, p, e)) & 0xFFFFFFFFz = v[p]p += 1y = v[0]v[n - 1] = (v[n - 1] + shift(z, y, x, k, p, e)) & 0xFFFFFFFFz = v[n - 1]return v
def decrypt(v, k):delta = 0x9E3779B9n = len(v)rounds = 6 + 52 // nx = (rounds * delta) & 0xFFFFFFFFy = v[0]for i in range(rounds):e = (x >> 2) & 3for p in range(n - 1, 0, -1):z = v[p - 1]v[p] = (v[p] - shift(z, y, x, k, p, e)) & 0xFFFFFFFFy = v[p]p -= 1z = v[n - 1]v[0] = (v[0] - shift(z, y, x, k, p, e)) & 0xFFFFFFFFy = v[0]x = (x - delta) & 0xFFFFFFFFreturn v
if __name__ == '__main__':plain = [1, 2]key = [2, 2, 3, 4]encrypted = encrypt(plain, key)print(encrypted)decrypted = decrypt(encrypted, key)print(decrypted)
"""
[3238569099, 2059193138]
[1, 2]
"""
示例代码
#include <stdio.h>
#include <stdint.h>
#define DELTA 0x9e3779b9
#define MX (((z>>5^y<<2) + (y>>3^z<<4)) ^ ((sum^y) + (key[(p&3)^e] ^ z)))void btea(uint32_t *v, int n, uint32_t const key[4])
{uint32_t y, z, sum;unsigned p, rounds, e;if (n > 1) /* Coding Part */{rounds = 6 + 52/n;sum = 0;z = v[n-1];do{sum += DELTA;e = (sum >> 2) & 3;for (p=0; p<n-1; p++){y = v[p+1];z = v[p] += MX;}y = v[0];z = v[n-1] += MX;}while (--rounds);}else if (n < -1) /* Decoding Part */{n = -n;rounds = 6 + 52/n;sum = rounds*DELTA;y = v[0];do{e = (sum >> 2) & 3;for (p=n-1; p>0; p--){z = v[p-1];y = v[p] -= MX;}z = v[n-1];y = v[0] -= MX;sum -= DELTA;}while (--rounds);}
}int main()
{uint32_t v[4]= {0x73647979,0x726b6f5f,0x646f675f,0x0};uint32_t const k[4]= {0X95C4C,0X871D,0X1A7B7,0X12C7C7};int n= 2; //n的绝对值表示v的长度,取正表示加密,取负表示解密// v为要加密的数据是两个32位无符号整数// k为加密解密密钥,为4个32位无符号整数,即密钥长度为128位printf("加密前原始数据:%s\n",(char*)v);btea(v, n, k);printf("加密后的数据:%u %u %u\n",v[0],v[1],v[3]);btea(v, -n, k);printf("解密后的数据:%s\n",(char*)v);return 0;
}
输出结果:
加密前原始数据:yyds_okr_god
加密后的数据:609835868 2980644312 0
解密后的数据:yyds_okr_god
四.逆向中TEA系列加密的识别
解决逆向题大部分出现TEA的场合都是【识别算法->编写对应解密程序】
分析二进制文件中的算法的时候有几个识别的特征
- 可能存在针对64bit以及128bit数字的操作(输入的msg和key) ,一般会用无符号的32位的数组表示
- 存在先进行位移,然后异或的类似操作(
(z>>5^y<<2)这类混合变换)(z>>5^y<<2)就是xxtea加密了,** - 存在(v0 << 4)** 和 (v0 >> 5)移位就是tea和xtea加密了
- 前面一个复杂的混合变换的结果可能会叠加到另一个值上,两者相互叠加(Feistel 结构)
- 获取密钥的时候,会使用某一个常量值作为下标(
key[(sum>>11) & 3])存在轮换的方式获得密钥 就是xtea或者xxtea了 - 会在算法开始定义一个delta,并且这个值不断的参与算法,但是从来不会受到输入的影响(delta数值如果没有魔改就是0x9e3779b9)
- 如果出现了0x9e3779b9这个数字一般就能确定是TEA加密系列
五.解题实例
NSSCTF/算法识别/工坊第四题TEA
一个txt文件
hint1 = {11,22,33,44}
hint2 = {0x7c12e17f,0x43c2b691,0xa8d8d6ce,0x6280ecc8,0xe6e18c6e,0x20d6dfa3,0xf2dd40c,0xb819b77e,0xb9258436,0x5d3e88b6}
.text:0000000000401550 ; unsigned int *__fastcall encrypt(unsigned int *, unsigned int *)
.text:0000000000401550 public _Z7encryptPjS_
.text:0000000000401550 _Z7encryptPjS_ proc near ; CODE XREF: main+FC↓p
.text:0000000000401550 ; DATA XREF: .pdata:000000000040A06C↓o
.text:0000000000401550
.text:0000000000401550 var_14= dword ptr -14h
.text:0000000000401550 var_10= dword ptr -10h
.text:0000000000401550 var_C= dword ptr -0Ch
.text:0000000000401550 var_8= dword ptr -8
.text:0000000000401550 var_4= dword ptr -4
.text:0000000000401550 arg_0= qword ptr 10h
.text:0000000000401550 arg_8= qword ptr 18h
.text:0000000000401550
.text:0000000000401550 55 push rbp
.text:0000000000401551 48 89 E5 mov rbp, rsp
.text:0000000000401554 48 83 EC 20 sub rsp, 20h
.text:0000000000401558 48 89 4D 10 mov [rbp+arg_0], rcx
.text:000000000040155C 48 89 55 18 mov [rbp+arg_8], rdx
.text:0000000000401560 C7 45 EC B9 79 37 9E mov [rbp+var_14], 9E3779B9h
.text:0000000000401567 48 8B 45 10 mov rax, [rbp+arg_0]
.text:000000000040156B 8B 00 mov eax, [rax]
.text:000000000040156D 89 45 FC mov [rbp+var_4], eax
.text:0000000000401570 48 8B 45 10 mov rax, [rbp+arg_0]
.text:0000000000401574 8B 40 04 mov eax, [rax+4]
.text:0000000000401577 89 45 F8 mov [rbp+var_8], eax
.text:000000000040157A C7 45 F4 00 00 00 00 mov [rbp+var_C], 0
.text:0000000000401581 C7 45 F0 00 00 00 00 mov [rbp+var_10], 0
.text:0000000000401581
.text:0000000000401588
.text:0000000000401588 loc_401588: ; CODE XREF: encrypt(uint *,uint *)+B2↓j
.text:0000000000401588 83 7D F0 1F cmp [rbp+var_10], 1Fh
.text:000000000040158C 7F 76 jg short loc_401604
.text:000000000040158C
.text:000000000040158E 8B 45 EC mov eax, [rbp+var_14]
.text:0000000000401591 01 45 F4 add [rbp+var_C], eax
.text:0000000000401594 8B 45 F8 mov eax, [rbp+var_8]
.text:0000000000401597 C1 E0 04 shl eax, 4
.text:000000000040159A 89 C2 mov edx, eax
.text:000000000040159C 48 8B 45 18 mov rax, [rbp+arg_8]
.text:00000000004015A0 8B 00 mov eax, [rax]
.text:00000000004015A2 01 C2 add edx, eax
.text:00000000004015A4 8B 4D F8 mov ecx, [rbp+var_8]
.text:00000000004015A7 8B 45 F4 mov eax, [rbp+var_C]
.text:00000000004015AA 01 C8 add eax, ecx
.text:00000000004015AC 31 C2 xor edx, eax
.text:00000000004015AE 8B 45 F8 mov eax, [rbp+var_8]
.text:00000000004015B1 C1 E8 05 shr eax, 5
.text:00000000004015B4 89 C1 mov ecx, eax
.text:00000000004015B6 48 8B 45 18 mov rax, [rbp+arg_8]
.text:00000000004015BA 48 83 C0 04 add rax, 4
.text:00000000004015BE 8B 00 mov eax, [rax]
.text:00000000004015C0 01 C8 add eax, ecx
.text:00000000004015C2 31 D0 xor eax, edx
.text:00000000004015C4 01 45 FC add [rbp+var_4], eax
.text:00000000004015C7 8B 45 FC mov eax, [rbp+var_4]
.text:00000000004015CA C1 E0 04 shl eax, 4
.text:00000000004015CD 89 C2 mov edx, eax
.text:00000000004015CF 48 8B 45 18 mov rax, [rbp+arg_8]
.text:00000000004015D3 48 83 C0 08 add rax, 8
.text:00000000004015D7 8B 00 mov eax, [rax]
.text:00000000004015D9 01 C2 add edx, eax
.text:00000000004015DB 8B 4D FC mov ecx, [rbp+var_4]
.text:00000000004015DE 8B 45 F4 mov eax, [rbp+var_C]
.text:00000000004015E1 01 C8 add eax, ecx
.text:00000000004015E3 31 C2 xor edx, eax
.text:00000000004015E5 8B 45 FC mov eax, [rbp+var_4]
.text:00000000004015E8 C1 E8 05 shr eax, 5
.text:00000000004015EB 89 C1 mov ecx, eax
.text:00000000004015ED 48 8B 45 18 mov rax, [rbp+arg_8]
.text:00000000004015F1 48 83 C0 0C add rax, 0Ch
.text:00000000004015F5 8B 00 mov eax, [rax]
.text:00000000004015F7 01 C8 add eax, ecx
.text:00000000004015F9 31 D0 xor eax, edx
.text:00000000004015FB 01 45 F8 add [rbp+var_8], eax
.text:00000000004015FE 83 45 F0 01 add [rbp+var_10], 1
.text:0000000000401602 EB 84 jmp short loc_401588
.text:0000000000401602
.text:0000000000401604 ; ---------------------------------------------------------------------------
.text:0000000000401604
.text:0000000000401604 loc_401604: ; CODE XREF: encrypt(uint *,uint *)+3C↑j
.text:0000000000401604 48 8B 45 10 mov rax, [rbp+arg_0]
.text:0000000000401608 8B 55 FC mov edx, [rbp+var_4]
.text:000000000040160B 89 10 mov [rax], edx
.text:000000000040160D 48 8B 45 10 mov rax, [rbp+arg_0]
.text:0000000000401611 48 83 C0 04 add rax, 4
.text:0000000000401615 8B 55 F8 mov edx, [rbp+var_8]
.text:0000000000401618 89 10 mov [rax], edx
.text:000000000040161A 90 nop
.text:000000000040161B 48 83 C4 20 add rsp, 20h
.text:000000000040161F 5D pop rbp
.text:0000000000401620 C3 retn
.text:0000000000401620
.text:0000000000401620 _Z7encryptPjS_ endp
识别为tea(通过hint1,有四个数字,
hint2有4x10=40位,大概的fllag的长度
逆向加密函数中有左移右移,四个异或,脚本直接解
出现9E3779B9h,大概是delta
#include<stdio.h>
#include <stdint.h>
#include<string.h>void encrypt(uint32_t *v, uint32_t *k) {uint32_t v0 = v[0], v1 = v[1], sum = 0, i;uint32_t delta = 0x9e3779b9;for (i = 0; i < 32; i++) {sum += delta;v0 += ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);v1 += ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);}v[0] = v0; v[1] = v1;
}void decrypt(uint32_t *v, uint32_t *k) {uint32_t v0 = v[0], v1 = v[1], i;uint32_t delta = 0x9e3779b9;uint32_t sum = delta * 32;for (i = 0; i < 32; i++) {v1 -= ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);v0 -= ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);sum -= delta;}v[0] = v0; v[1] = v1;
}int main() {// 提供的提示数组uint32_t key[4] = {11, 22, 33, 44};uint32_t v[10] = {0x7c12e17f, 0x43c2b691, 0xa8d8d6ce, 0x6280ecc8, 0xe6e18c6e, 0x20d6dfa3, 0xf2dd40c, 0xb819b77e, 0xb9258436, 0x5d3e88b6};uint32_t temp[2]; //定义存放解密后的值for(int i=0;i<10;i+=2)
{temp[0] = v[i];temp[1] = v[i+1];decrypt(temp, key);for(int j = 0; j < 2; j++){printf("%c", temp[j]&0xff);printf("%c", (temp[j]>>8)&0xff);printf("%c", (temp[j]>>16)&0xff);printf("%c", (temp[j]>>24)&0xff);}
}return 0;
}//NSSCTF{5b84a51236d7043fe2480d69d24b37a3}
NSSCTF/算法识别/工坊第五题XXTEA
给了一个py文件和一个so文件,
from ctypes import c_uint32DELTA = 0x9E3779B9
def decrypt(v, n, k):rounds = 6 + int(52 / n)sum = c_uint32(rounds * DELTA)y = v[0].valuewhile rounds > 0:e = (sum.value >> 2) & 3p = n - 1while p > 0:z = v[p - 1].valuev[p].value -= (((z >> 5 ^ y << 2) + (y >> 3 ^ z << 4)) ^ ((sum.value ^ y) + (k[(p & 3) ^ e] ^ z)))y = v[p].valuep -= 1z = v[n - 1].valuev[0].value -= (((z >> 5 ^ y << 2) + (y >> 3 ^ z << 4)) ^ ((sum.value ^ y) + (k[(p & 3) ^ e] ^ z)))y = v[0].valuesum.value -= DELTArounds -= 1if __name__ == "__main__":k = [0x73645212, 0x31378432, 0x12325153, 0x34356531]m = [c_uint32(0xe034b77),c_uint32(0xfec9c3af),c_uint32(0x763b3820),c_uint32(0x8bdcc362),c_uint32(0xf443f322),c_uint32(0x6a0759bb),c_uint32(0x8d67f594),c_uint32(0x320282e4),c_uint32(0xef25b93c),c_uint32(0x4cad32cd)]decrypt(m, len(m), k)for i in m:for j in range(4):print(chr(i.value&0xff),end='')i.value >>= 8#NSSCTF{c166910265954e79448a6a1d80ea4bfb}
tea就先这样,再死啃就失去兴趣,现在多学一点基础知识,多了解一点,入门之后再慢慢来