Datawhale X 李宏毅苹果书 AI夏令营 深度学习01

神经网络的优化，通常我们使用梯度下降的方法对获取最优的参数，已达到优化神经网络的目的。另外，我们也可以对学习率进行调整，通过使用自适应学习率和学习率调度，最后，批量归一化改变误差表面，达到优化的目的。

同样，也会存在优化失败的时候，在收敛在局部极限值或者鞍点的时候，会导致优化失败。

局部最小值和鞍点

做参数优化的时候，我们总是希望，随着参数不断更新，训练的损失不断下降，最后收敛到我们可以接受的期望的值。但是经常会出现，随着参数的更新，训练损失不再下降，而这时的损失还达不到我们的期望，这个时候，很可能就遇到的局部最小值点，或者鞍点。

如图：

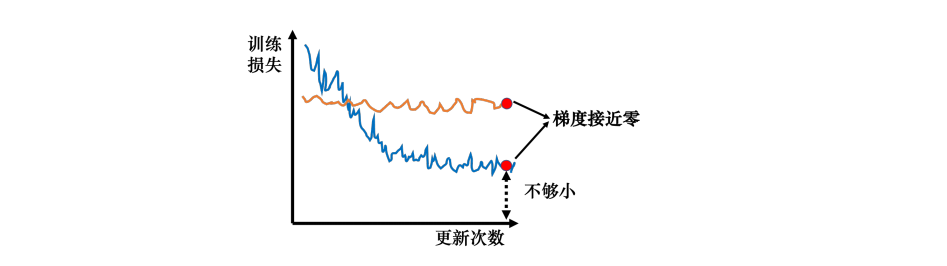
局部最小值与鞍点的异同

我们知道在做深度学习的时候，梯度下降收敛到局部最小值，此时梯度为零。但是并不是所有梯度为零的点都是局部最小值点，比如鞍点，

如图：

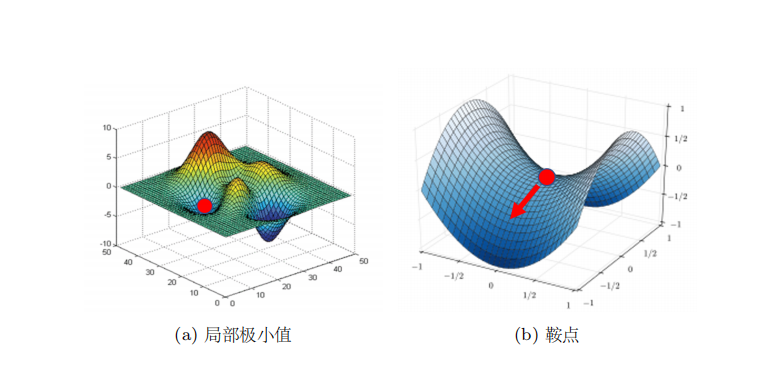
我们把梯度为零的点称为临界点。为什么要区分局部最小值点和鞍点呢？

• 当梯度为零时：在局部最小值点，我们不管往哪个方向走，梯度都会上升，但是鞍点不会，鞍点在局部最小值和最大值之间，在鞍点处，我们可以想办法让损失更低。

逃离鞍点

所以，只要我们遇到的是鞍点，那么我总能找到一个方向去更新参数，然后获得比鞍点更小的损失。

在一维空间的误差表面上，有一个局部最小值，但是在二维空间上，它可能就只是一个鞍点，也就是说当前空间中我们遇到的局部最小值点，在更高维空间中，可能是鞍点，我们就能找到是损失下降的更新参数的方向。

我们在训练一个神经网络的时候，会有很多参数，多大百万千万级，所以误差表面有非常高的维度，非常的复杂。(参数的数量代表了误差表面的维度)。所以我遇到的点很大的可能都是鞍点，而不是局部最小值点。

我们常常会遇到两种情况：损失仍然很高，却遇到了临界点而不再下降；或者损失降得很低，才遇到临界点。

批量和动量

用来学习训练的数据集通常数据量非常大，如果以全部数据为对象求损失函数的值，计算会花费很长的时间，算几千万数据的损失函数的和，是不现实的。因此我们会从全部数据中选取出一部分，作为全部数据的““近似””，这部分数据被称为一个批量(batch)，数据被分成很多个批量，遍历所有批量的过程被称为一个回合(epoch)。并且在分成批量的时候将数据打乱(shuffle)。

如图：

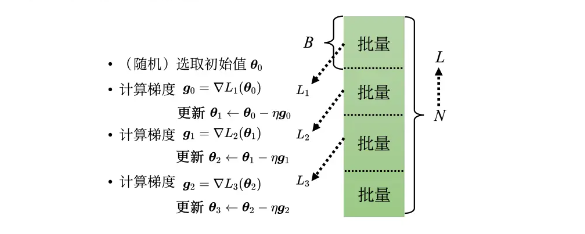
批量大小对梯度下降的影响

批量大小（Batch Size）

1. 收敛速度：

• 较小的批量大小通常可以提供更频繁的权重更新，这有助于模型更快地收敛，因为每次更新都是基于最新的数据信息。

2. 内存使用：

• 较小的批量大小意味着每次只处理少量数据，这减少了对内存的需求，使得可以在内存有限的系统上训练更大的模型。

3. 计算效率：

• 较大的批量大小可以提高计算效率，因为现代硬件（如GPU）可以并行处理大量数据。较小的批量可能无法充分利用这些硬件的并行处理能力。

4. 泛化能力：

• 使用较小批量大小的训练过程可能更不稳定，但有时可以导致更好的泛化能力，因为它允许模型从更多的数据扰动中学习。

5. 训练稳定性：

• 较大的批量大小可以提供更平滑的梯度估计，从而减少训练过程中的噪声和振荡，使得训练过程更稳定。

6. 局部最小值和鞍点：

• 较大的批量大小可能使模型更容易陷入局部最小值或鞍点，因为它们提供了更准确的梯度估计，但这也可能导致模型错过更优的全局最小值。

7. 训练成本：

• 较小的批量大小可能需要更多的迭代次数来达到相同的损失水平，这可能会增加训练成本，尤其是在需要大量计算资源的情况下。

8. 超参数调整：

• 批量大小的选择可能影响其他超参数（如学习率）的调整。例如，较大的批量大小可能需要较小的学习率来防止权重更新过大。

9. 数据多样性：

• 在使用小批量训练时，每次更新都可能基于不同的数据样本，这有助于模型学习到数据的多样性。

10. 过拟合风险：

• 使用较大的批量大小可能会增加过拟合的风险，因为模型可能会过度适应训练数据中的特定模式。

动量法

引用《深度学习详解》

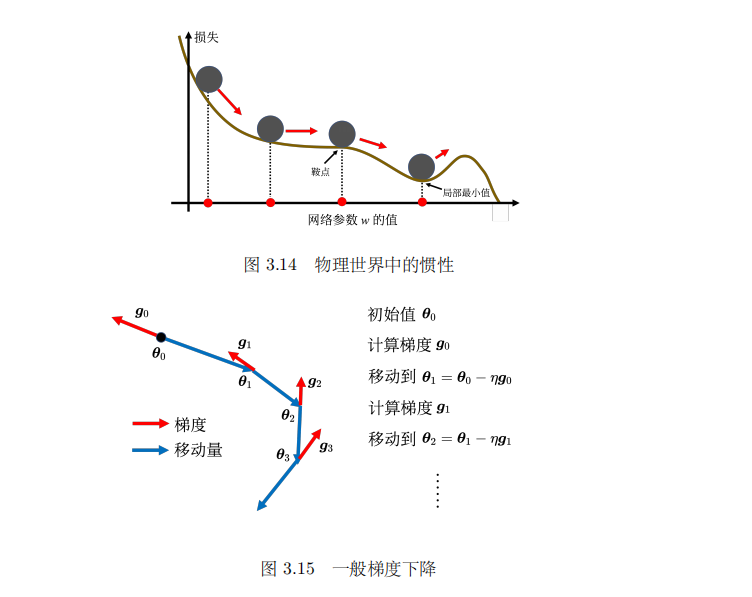
动量法（momentum method）是另外一个可以对抗鞍点或局部最小值的方法。如图3.14
所示，假设误差表面就是真正的斜坡，参数是一个球，把球从斜坡上滚下来，如果使用梯度
下降，球走到局部最小值或鞍点就停住了。但是在物理的世界里，一个球如果从高处滚下来，
就算滚到鞍点或鞍点，因为惯性的关系它还是会继续往前走。如果球的动量足够大，其甚至翻
过小坡继续往前走。因此在物理的世界里面，一个球从高处滚下来的时候，它并不一定会被
鞍点或局部最小值卡住，如果将其应用到梯度下降中，这就是动量。

如图：

动量法（Momentum Method）是一种在梯度下降优化算法中使用的技巧，旨在加速梯度下降的收敛速度，特别是在处理具有大量参数的深度学习模型时。动量法的核心思想是利用过去梯度的信息来调整当前的梯度更新，从而减少训练过程中的振荡，并帮助模型更快地收敛到最小损失值。

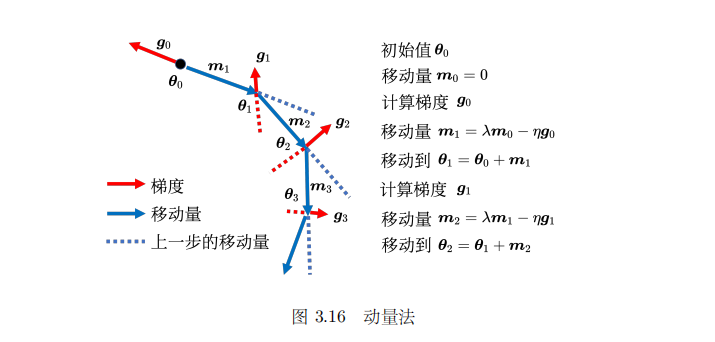
动量法的关键点：

1. 动量项（Velocity）：
   动量法引入了一个动量项，它是一个累积的梯度平均值，可以看作是参数更新的“惯性”。

2. 动量系数（Momentum Coefficient）：
   动量系数（通常表示为γ或β）是一个介于0和1之间的超参数，它决定了动量项在更新中所占的权重。较高的动量系数意味着过去的梯度信息在更新中占更大的比重。

3. 更新规则：
   动量法的参数更新规则如下：

\[v_{t+1} = \gamma v_t + \eta \cdot \nabla J(\theta_t) \]

\[\theta_{t+1} = \theta_t - v_{t+1} \]

其中，\(v\) 是动量项，\(\eta\)是学习率，\(\nabla J(\theta_t)\) 是当前参数的梯度，\(\theta\) 是模型参数。

4. 减少振荡：
   动量法通过平滑梯度的方向，减少了在梯度下降过程中的振荡，特别是在梯度方向频繁变化的情况下。

5. 加速收敛：
   当梯度的方向在连续的迭代中保持一致时，动量项会逐渐增加，从而加速参数的更新，使模型更快地收敛。

6. 避免局部最小值和鞍点：
   动量法有助于模型跳出局部最小值和鞍点，因为它允许模型在梯度方向上获得更大的更新步长。

7. 超参数调整：
   动量法中的动量系数需要仔细调整，以确保动量项不会过大或过小，影响模型的收敛性。

8. Nesterov加速梯度（NAG）：
   Nesterov加速梯度是动量法的一个变体，它在计算动量项时考虑了参数的下一次更新，从而进一步加速收敛。