\(\large\mathfrak{1st.\ Preamble|}\) 前言
题目传送门:P3210 [HNOI2010] 取石头游戏)
主要是参考楼下大佬的题解,对于其中没讲到或比较难懂的地方进行讲解,以及配上了图。
\(\large\mathfrak{2nd.\ Solution|}\) 题解
楼下大佬的比喻十分形象生动地描绘了俩人去石头的过程:
取石子的过程可以转化为两端分别有一个栈,可以从栈顶取石子,中间有若干个双端队列,可以从其两端取石子。
我们可以根据俩人取石子的过程推算出先手积分减去后手积分的差值 \(dif\),然后根据总和就能求出最终俩人的积分。先手肯定希望 \(dif\) 尽可能大,后手肯定希望 \(dif\) 尽可能小。
Q:为什么是算差值而不是直接算积分?
A:因为差值好算呗!等会你就知道了。
为了方便计算,我们肯定希望每次的全局最大权值的位置都是可以直接取的。接下来我们分两个部分讨论这俩人取石子的过程。
注:接下来的递减、递增均指非严格递减和递增。
中间部分(双端队列)
对于每个中间区块(双端队列)中,权值递增、递减和下凹的情况都很好解决,如下图箭头所示,从其中一端或两端开始取就行。
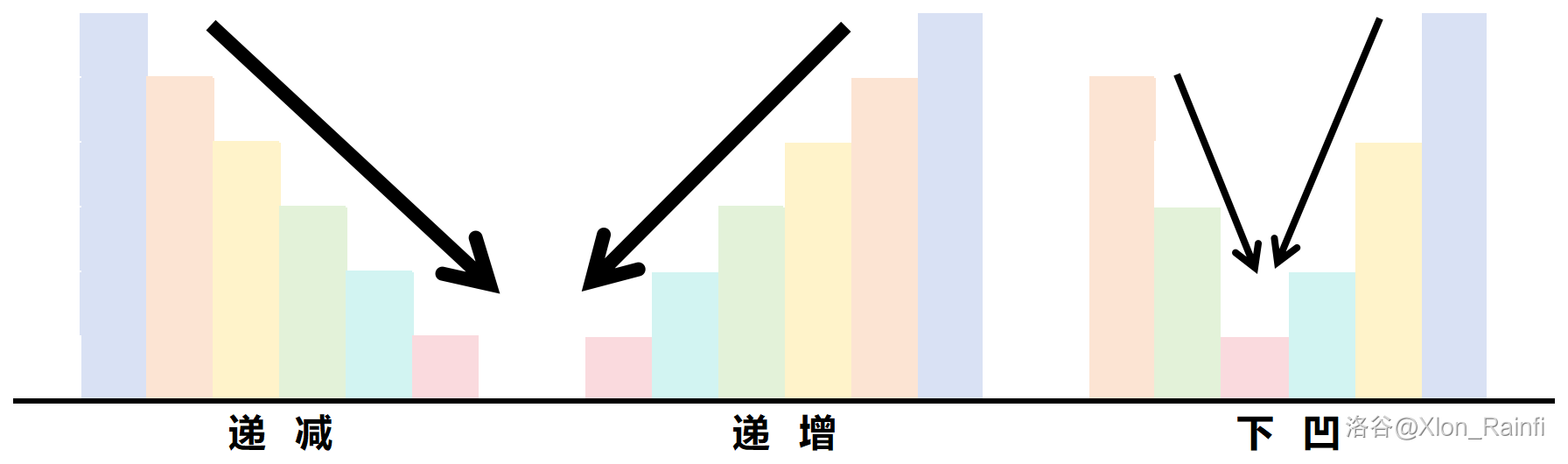
然后我们来看看上凸该如何解决。
我们先来考虑最简单的三个位置的上凸情况:若存在 \(a_{i-1}\le a_i\) 并且 \(a_i\ge a_{i+1}\),若当前最优选择为 \(a_{i-1}\),则先手会选择 \(a_{i-1}\),接着后手会选择 \(a_i\),然后先手会选择 \(a_{i+1}\),最终 \(dif\) 会增加(或减少)\(a_{i-1}-a_i+a_{i+1}\),于是我们就可以把 \(a_{i-1}, a_i, a_{i+1}\) 三个位置打包成一个权值为 \(a_{i-1}-a_i+a_{i+1}\) 的位置。反之同理。这也是为什么我们是算差值而不是直接算积分。
当我们把每个上凸都打包完,剩下就只剩下上面的三种情况,当前最大都是可以直接取到的。
两端(栈)
对于左边部分,我们希望是单调递增的(因为只能从中间往外取);反之,对于右边部分,我们希望是单调递减的。
左边部分中,若存在递减的部分,那我们可以像刚才一样,将其打包起来,即:若存在 \(a_i>=a_{i+1}\),且 \(a_{i+1}\) 为目前全局最优,因为先手只能从右侧开始选,所以先手比选 \(a_{i+1}\),后手必选 \(a_i\),于是我们可以把 \(a_i\) 和 \(a_{i+1}\) 打包成一个权值为 \(a_{i+1}-a_i\) 的位置。
右边部分同理。
实现方法
全部打包完后,接下来每次的全局最大值必定可以直接取到,所以我们可以直接将所有位置按权值从大到小排序,然后从大到小取即可。
\(\large\mathfrak{3rd.\ Code|}\) 代码
代码中过于简单的细节就不标注了。敢做黑题的相信一定能看懂。
#include <bits/stdc++.h>
#define ll long long
#define FOR(i,l,r) for(int i=l;i<=r;i++)
#define FILE(x) freopen(x".in","r",stdin),freopen(x".out","w",stdout);
#define pii pair<int,int>
#define pll pair<long long,long long>
// #define Clock
using namespace std;
const ll N=2e6+10;
ll n,a[N],sum,l[N],r[N],L,R,p[N],cnt,s,ans;
bool book[N];
inline bool cmp(ll a,ll b){return a>b;}
int main(){#ifdef Clockclock_t Start_Time=clock();#endif// ios::sync_with_stdio(false);// cin.tie(0),cout.tie(0);// FILE("xxx");cin>>n; r[0]=1,l[n+1]=n;for(ll i=1;i<=n;i++){cin>>a[i];sum+=a[i],book[i]=a[i];l[i]=i-1,r[i]=i+1;}for(ll i=3;i<=n;i=r[i]){ll x=l[l[i]],y=l[i],z=i;while(book[x]&&book[y]&&book[z]&&a[y]>a[x]&&a[y]>a[z]){a[i]=a[x]+a[z]-a[y],r[l[x]]=i,l[i]=l[x];x=l[l[i]],y=l[i],z=i;}}L=r[0],R=l[n+1];while(a[L]>=a[r[L]]&&book[L]&&book[r[L]])s-=a[L]-a[r[L]],L=r[r[L]];while(a[R]>=a[l[R]]&&book[R]&&book[l[R]])s-=a[R]-a[l[R]],R=l[l[R]];for(ll i=L;i<=R;i=r[i])if(book[i])p[++cnt]=a[i];sort(p+1,p+cnt+1,cmp);p[++cnt]=s;for(ll i=1;i<=cnt;i++)ans+=(i%2?p[i]:-p[i]);cout<<(sum+ans)/2<<' '<<(sum-ans)/2;#ifdef Clockcout<<"\n- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -\nRuntime: "<<clock()-Start_Time<<" ms\n";system("pause");#endifreturn 0;
}
\(\large\mathfrak{4th.\ Postscript|}\) 后记
第一天写的时候没过,那时还是紫题,并且不能写题解。第二天过完后发现变成了黑题,而且还可以写题解!于是遍欣喜若狂地写下了这篇题解。