《深度学习详解》3.2节中关于批量和动量的主要内容总结:
批量的概念:在深度学习训练过程中,数据不是一次性全部用于计算梯度,而是被分成多个小批量(batch),每个批量包含一定数量的数据。每个批量的损失函数用于计算梯度并更新模型参数。
批量大小对梯度下降法的影响:
两种极端情况:
批量梯度下降法(Batch Gradient Descent, BGD):使用全部数据作为批量,计算稳定但每次更新需要等待所有数据处理完毕,计算量大。
随机梯度下降法(Stochastic Gradient Descent, SGD):批量大小为1,每次只用一个数据点更新参数,引入了随机性,更新方向可能会曲折,但有助于逃离局部最小值。
计算时间:考虑并行运算,批量大小较小时,完成一个回合的时间较长;批量大小较大时,GPU计算梯度并更新参数的时间会增加,但在一定范围内,如从1到1000,时间几乎相同。
训练效果:实验表明,过大的批量大小可能会导致模型在验证集上准确率降低,而小的批量梯度有噪声,但对训练和测试有帮助,能避免陷入局部最小值。
动量法(Momentum Method):一种改进的梯度下降方法,通过结合当前梯度和之前更新的方向来更新参数,有助于模型更快收敛,并且能够越过一些小的局部最小值或鞍点。
动量法的数学表达:动量\( m \)可以看作是之前所有梯度的加权和,更新规则可以表示为:
\[
m_{t} = \lambda m_{t-1} - \eta g_{t}
\]
其中,\( m_{t} \)是第\( t \)步的动量,\( \lambda \)是动量参数,\( \eta \)是学习率,\( g_{t} \)是第\( t \)步的梯度。
具体计算:每一步的移动方向由梯度反方向加上前一步移动方向决定,移动量可以表示为之前所有计算梯度的加权和。
动量法的优势:动量法可以增加参数更新的稳定性,减少震荡,有助于模型更快收敛到全局最小值。
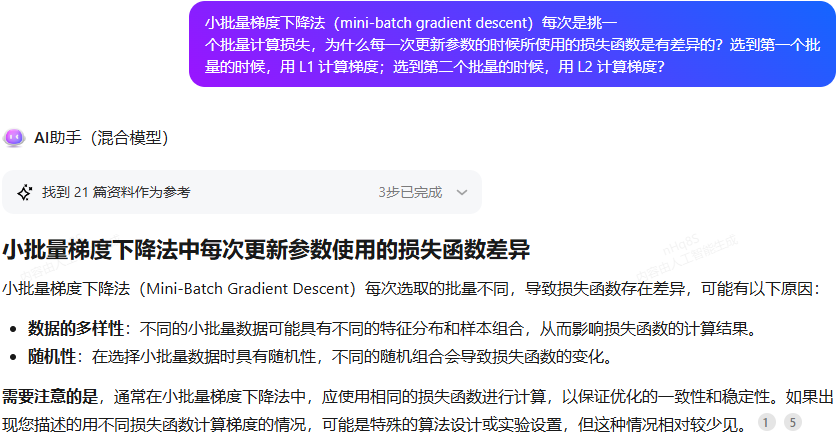
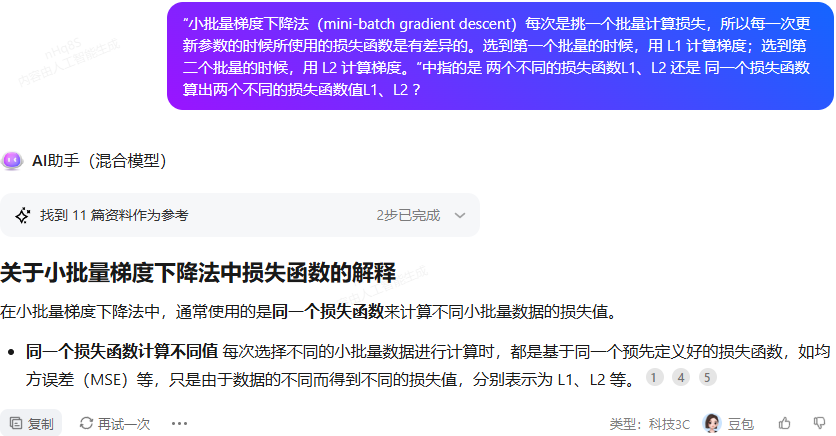
我关于3.2.1批量大小对梯度下降法的影响 的疑问
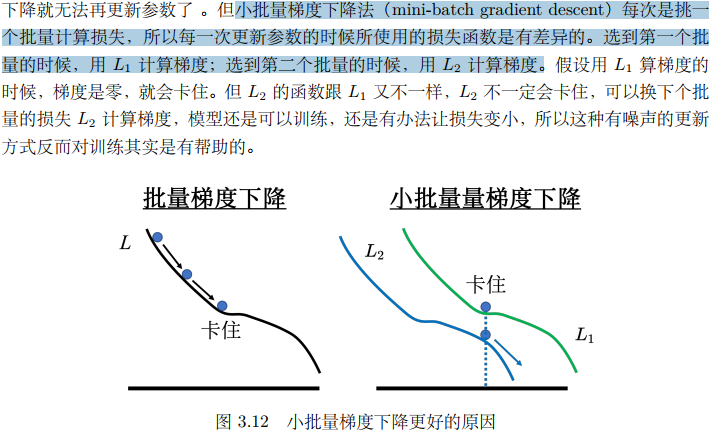
指的是 同一个损失函数算出两个不同的损失函数值L1、L2 还是 两个不同的损失函数L1、L2?问了LLM: