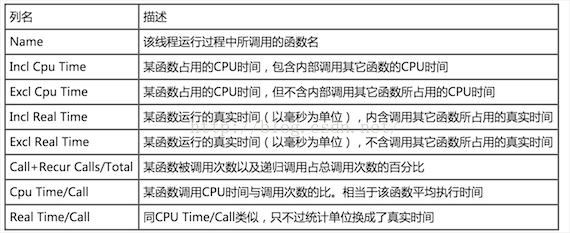
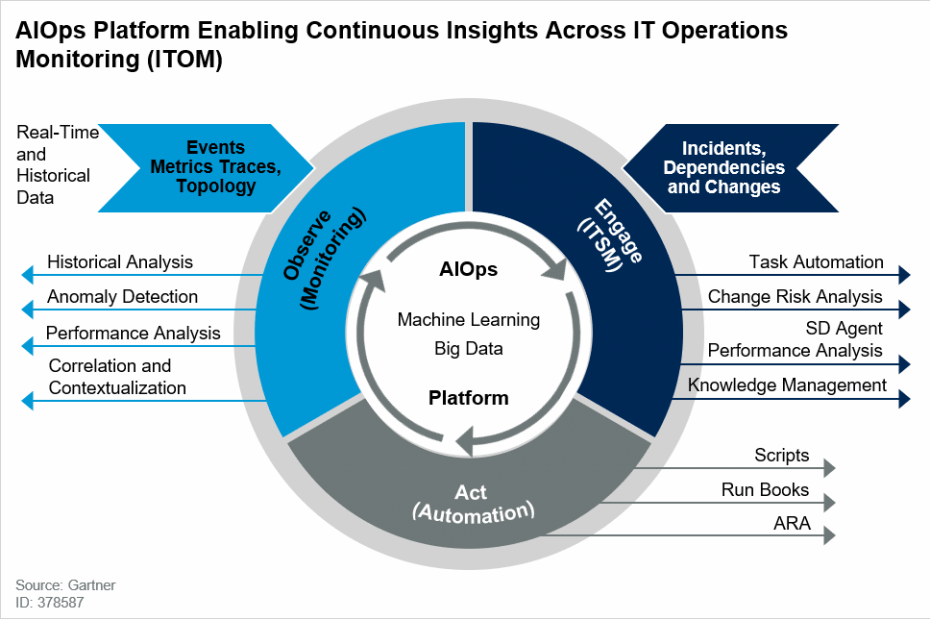
绪论:
今天主要讲RSA的原理以及python的实现,RSA的历史这些就不讲了,RSA的历史你自己去搜视频看才有趣,三个大佬创造的RSA。

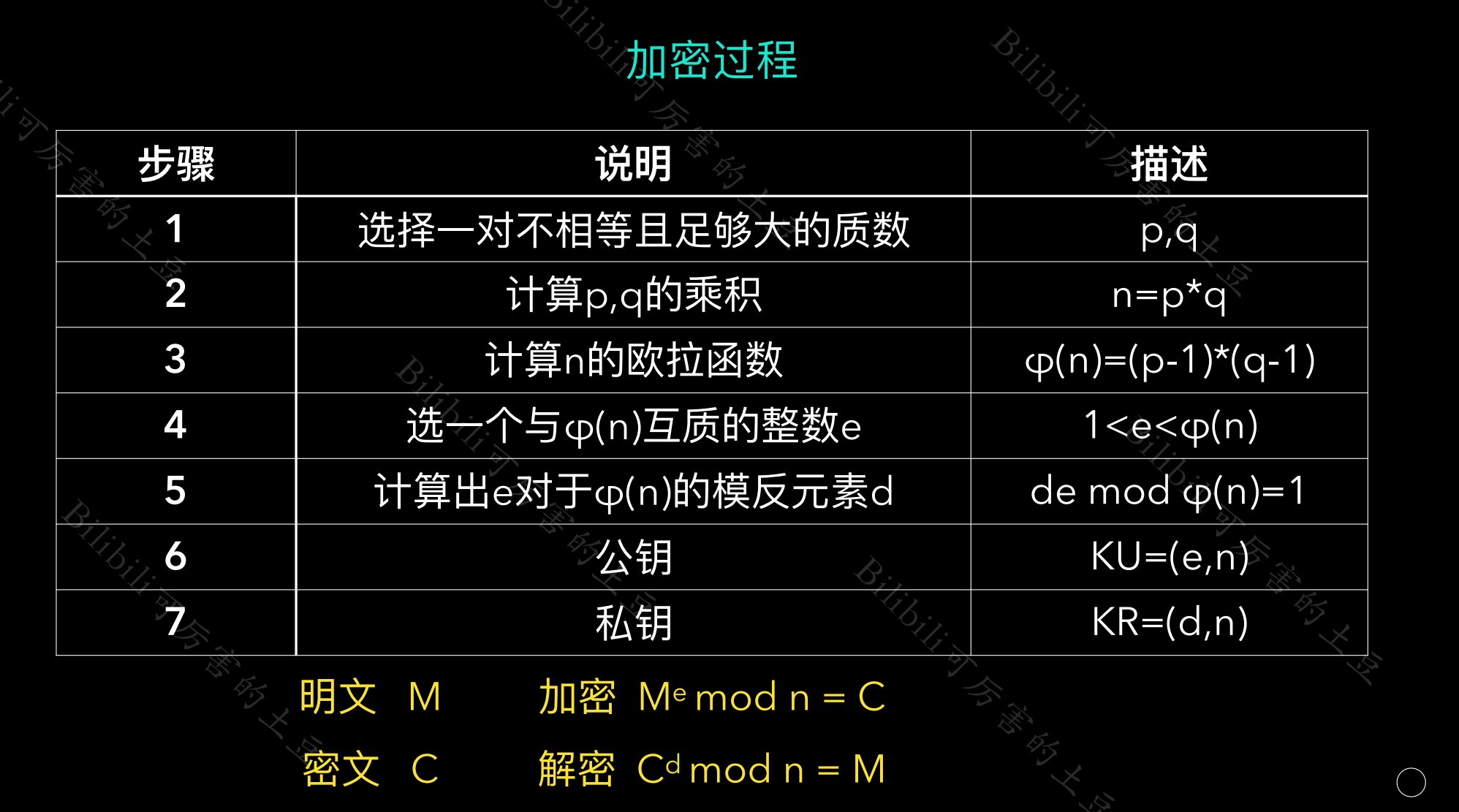
1.RSA加密过程
1.1选择p,q两个质数
(为什么选质数,后面就知道了,这里说一下学习方法:有一些步骤不知道为什么的,先看下去,可能后面会给你解答,不要死板,后面闲聊就没了,自己悟)
1.2计算p,q乘积
1.3计算n的欧拉函数

理解
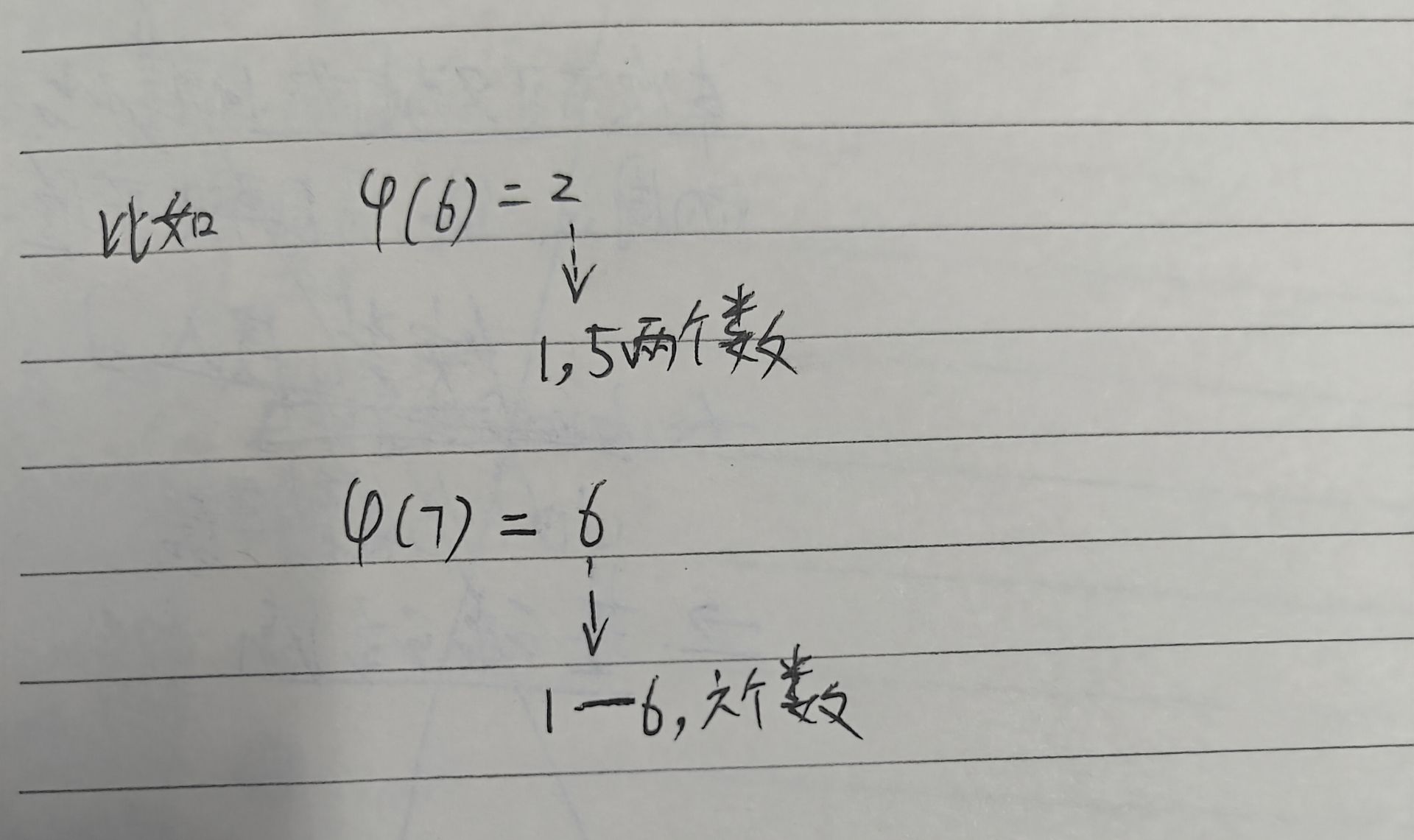

看了上面图解就知道应该为什么n的欧拉函数=(p-1)*(q-1)
1.4选一个与n的欧拉函数互质的数作为e
要求1<e<n的欧拉函数

(e是公钥一部分)
1.5计算模反元素d(RSA最重要部分)


理解
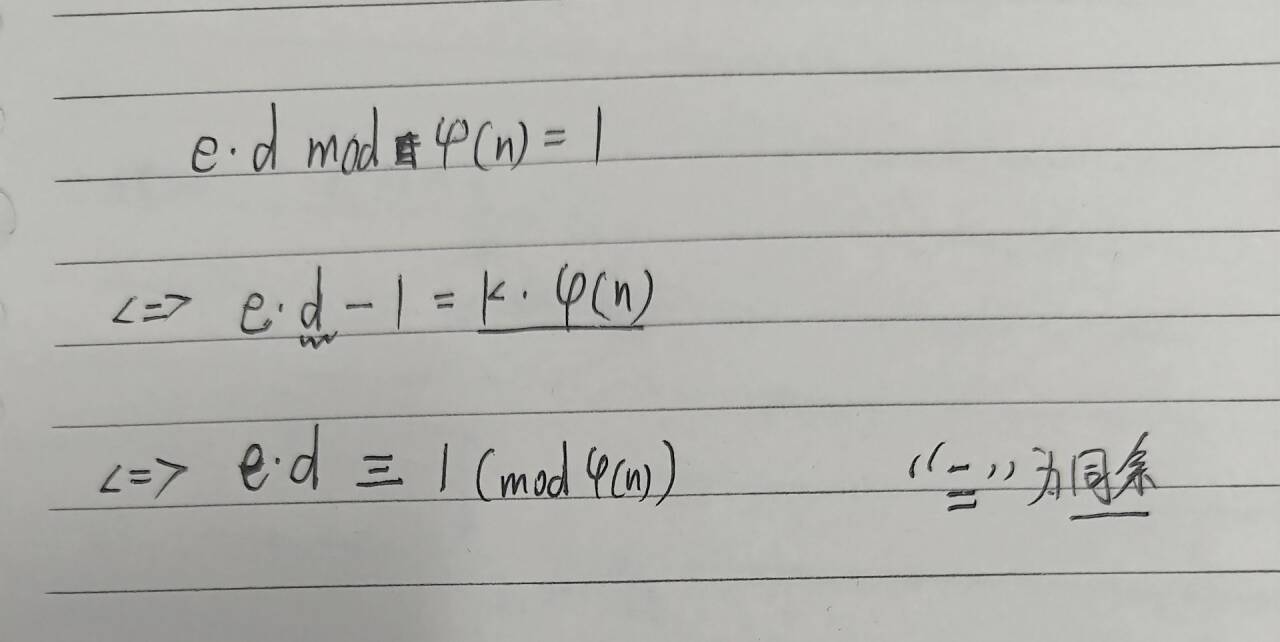
加密过程已经完成,现在验证解密
2.python实现RSA
我们发现RSA无外乎就是那几个参数之间的运算,而我们要做的便是使用Python实现这些算式,首先我们要做的第一步是
2.1生成两个大素数PP,QQ。
这是一个很模糊的概念,我希望各位在学习中能够做到尽量严谨,很显然,这里定义的大素数到底多大才是大呢?
10算大吗?100算吗?10000算吗?葛立恒数算吗?
我们需要一个更加精确的说法,我们生成两个512位的素数(这里包括之后的内容中涉及到的位都是指二进制位而不是十进制),那么如何使用Python产生一个素数呢,如果不借助任何外力的情况,我们可以从1开始选择,2,3,4…直到某个数满足512位且为素数为止,但是既然我们都使用Python了,为何还要这样做呢?
让我们来使用Python强大的开源库pycryptodome,一般来说你只需要使用
pip3 install pycryptodome
# 或
python3 -m pip install pycryptodome
便可以成功安装,然后在Python环境中执行以下代码
import Crypto
如果没有显示ModuleNotFoundError:等诸如此类的错误话,那么恭喜你成功的安装了本库。这里你可能会奇怪为什么安装使用pycryptodome,而引入时使用Crypto,这涉及到这的库和其他库的一些联系,有兴趣的可以自行去查找。
然后我们就可以生成素数了,我们引入库中的子包Crypto.Util.number,这个子包中包含了大量的数学工具,之后我们会经常用到这个子包。
from Crypto.Util.number import *
p = getPrime(512)
q = getPrime(512)
print(p)
print(q)
2.2 n=p⋅q, φ(n)=(p−1)(q−1)
后续的过程便简单了很多,我们只需要在之前的基础上完成运算即可,添加下列代码并执行
n = p*q
phi = (p-1)*(q-1)
2.3计算逆元d
选取与φ(n)φ(n)互素的e,计算满足ed≡1(modφ(n))ed≡1(modφ(n))
这里我们要完成两个数学操作,一个是互素的判断,一个是求解e的乘法逆元。
e = 65537
assert GCD(e, phi) == 1, "该e不满足互素条件"
d = inverse(e, phi)
这里GCD函数能够求解最大公因数(Greatest Common Divisor),之前我们学习了互素的概念就是两个数的最大公因数为1,所以这里我们用断言表达式认定ee一定是和phiphi互素的。为什么我们要选择65537作为e呢,实际上这并不是硬性规定,一些标准提供了一些ee的参考值,65537在各类实现与标准中被广泛使用,但是这并不影响你可以将值改变为其他值进行后续的操作。
求d的过程中,我们使用了inverse函数,该函数有两个参数(a,p),作用便是求解a在模p意义下的乘法逆元,那么这里我们便是求解e在模phi下面的乘法逆元,结果为d。之前我们提到了逆元是互为逆元,所以你可以尝试下面的代码
print(inverse(d, phi) == e)
2.4公钥和私钥
(n,e)即为公钥,(n,d)(n,d)即为私钥,此时我们便得到了一组RSA的公私钥,随后我们便可以开始用这组密钥来进行加解密操作
举例
加密:
假设我们要加密的消息为Hello,我们定义一个字符串进行存储
message = b'hello'
注意这里我们定义的是一个bytes类型字符串,它将每个字符用8位二进制进行存储,是字符串最原生的存储形式。你也可以直接定义'hello',但在Python3中它是一个Unicode的字符串,需要进行编码操作才能转换为bytes类型进行后续的运算。
但我们在RSA中是数与数的运算,该如何将字符串参与操作呢?
我们使用包中的bytes_to_long函数,从函数名也可以猜出来,这个函数是将字符串转换为数字,运行下列代码
m = bytes_to_long(message)
print(m)
此时,我们的消息已经被转换为一个字符串了。随后我们便可以对消息进行RSA加密
c = pow(m, e, n)
print(c)
我们使用Python自带的pow函数进行幂运算,注意不要写成m**e % n,二者代表的意义相同,但是pow函数内置快速幂,可以快速得出结果,而m**e % n会将meme的结果先计算出来再取模,meme是一个非常大的数,这会消耗你计算机大量的运算和存储资源。
至此,我们便完成了加密过程,得到了RSA的密文C。
解密:
msg = pow(c, d, n)
print(msg)
完整代码
from Crypto.Util.number import * #这个是关于RSA很多函数的库
p = getPrime(512) #111RSA第一步:生成随机的512位(二进制位 )p q
q = getPrime(512)
n = p*q #生成n
phi = (p-1)*(q-1) #欧拉函数
e = 65537 #公钥
assert GCD(e, phi) == 1, "该e不满足互素条件" #查看e 与 欧拉函数是否互质
d = inverse(e, phi) #求逆元dprint(f'公钥:({e}, {n})') #查看公钥
print(f'私钥:({d}, {n})') #查看私钥message = b'hello_RSA' #让明文转换为字符串
m = bytes_to_long(message) #将字符串转换为整数
print('消息:', m)c = pow(m, e, n) #加密 m的e次幂在模n下msg = pow(c, d, n) #解密 c的d次幂在模n下
print('明文整数:', msg) #明文mmw = long_to_bytes(msg)
print('明文整数:', mw)
assert msg == m, "解密失败"
有注释帮助理解
3.后续计划
8.28之后一周,学习完RSA基础再加上题巩固,就这样,一点点攻克。
结语:
无论学习的怎么样,理解了多少,不要管,对于我来说,刚刚接触的,理解了50%已经非常帅气了,坚持才是最重要的,不懂可以再找文章学习,不懂可以再问,反正就是方法总比困难多。下课
可能省赛之后会写md文件笔记,现在没有精力去弄
资料来源于:
B站博主/可厉害的土豆
Xenny师傅
若文章有错误,请见谅! 联系作者更改





![P10786 [NOI2024] 百万富翁](https://img2024.cnblogs.com/blog/3204443/202408/3204443-20240828224024278-1423842106.png)