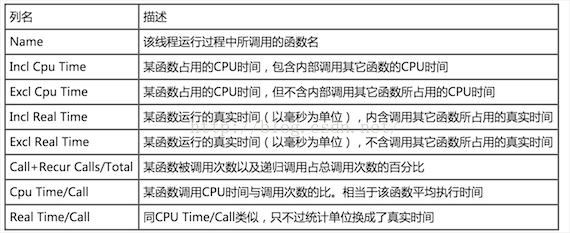
思路:
先考虑 Sub1 的部分分,暴力算法:
暴力询问所有 \(i<j\) 的数对 \((i,j)\)。
则一个 \(i\) 为最大值当且仅当 \((i,j)\) 的返回值都是 \(i\) 且在 \(i\) 之前没有满足此条件的位置。
则设 \(\operatorname{F}(n) = \frac{n(n-1)}{2}\) 表示暴力找出 \(n\) 个数中的最大值需要的询问次数,注意到 \(\operatorname{F}(1000) = 499500\),故可以通过 Sub1。
对于 Sub2,直接暴力肯定是不行的,但是注意到 \(t\) 的值开大了,故我们没必要一步到位,可以逐步缩小范围。
定义 \(\operatorname{W}(a,b)\) 表示原先最大值候选有 \(a\) 个,经过一次请求筛到 \(b\) 个候选人的最小询问次数;考虑分为 \(b\) 组,每组有 \(\lfloor \frac{a}{b} \rfloor \sim \lceil \frac{a}{b} \rceil\) 人,故:
现在我们的目的就是找到一个合理的筛检最大值候选的序列 \(h\),使得长度 \(len \le t\) 且 \(\sum\limits_{i=1}^{len-1} \operatorname{W}(h_i,h_{i+1}) \le s\)。
爆搜经过实测可以搜到 \(t=9\) 的情况,在 \(t=8\) 时几乎无法跑出来。
考虑动态规划算法,令 \(dp_{i,j}\) 表示 \(W_i = j\) 的情况下的最小询问数,则状态转移方程为:
时间复杂度为 \(O(tn^2)\),大概有 \(10^{13}\),按照最低预算,计算机 1s 可以跑 \(10^8\),则 \(\frac{10^{13}}{10^{8}} = 10^5\),则 \(\frac{10^5}{64^2} \approx 24\),大概要跑 \(1\) 天的时间,是肯定不行的。
可以有一个猜想,每次候选人的数量至少要减半,这样一定不会太劣,这样我们就将范围个缩小了,对于 \(dp_{i,j}\) 有效的 \(j\) 只有 \(\frac{n}{2^{i-1}}\),枚举的 \(k\) 大概是 \((j,2j]\),这样大概可以缩到 \(10^{11}\) 左右,可以在 1h 内跑完。
最后根据我们得到的 \(h\) 模拟一下分组求最大值的过程即可。
单组数据时间复杂度最多为 \(O(Nt)\)。
完整代码:
#include<bits/stdc++.h>
#define Add(x,y) (x+y>=mod)?(x+y-mod):(x+y)
#define lowbit(x) x&(-x)
#define pi pair<ll,ll>
#define pii pair<ll,pair<ll,ll>>
#define iip pair<pair<ll,ll>,ll>
#define ppii pair<pair<ll,ll>,pair<ll,ll>>
#define fi first
#define se second
#define full(l,r,x) for(auto it=l;it!=r;it++) (*it)=x
#define Full(a) memset(a,0,sizeof(a))
#define open(s1,s2) freopen(s1,"r",stdin),freopen(s2,"w",stdout);
#define For(i,l,r) for(int i=l;i<=r;i++)
#define _For(i,l,r) for(int i=r;i>=l;i--)
using namespace std;
typedef double db;
typedef unsigned long long ull;
typedef long long ll;
const int maxn=1e6+10;
std::vector<int> ask(std::vector<int> a, std::vector<int> b);
int n;
vector<int> a,b,h;
namespace Sub1{int cnt=0;int work(){a.clear(),b.clear();cnt=0;vector<int> l(n,0),r(n,0);For(i,0,n-1){l[i]=cnt;For(j,i+1,n-1){a.push_back(i);b.push_back(j);++cnt;}r[i]=cnt-1;}h=ask(a,b);For(i,0,n-1){bool F=1;For(j,l[i],r[i]){if(h[j]!=i){F=0;break;}}if(F)return i;}return 0;}
};
namespace Sub2{int cnt=0;int s[maxn];vector<int> E[maxn];stack<int> S;int p[]={1000000,500000,250000,125000,62498,20832,3472,183,1};void solve(int x){s[x]=a.size();int n=E[x].size();For(i,0,n-1){For(j,i+1,n-1){a.push_back(E[x][i]);b.push_back(E[x][j]);}}}int get(int x){int g=s[x],n=E[x].size();For(i,0,n-1){bool F=1;For(j,i+1,n-1)if(h[g++]!=E[x][i])F=0;if(F)return E[x][i];}return 0;}void get(int X,int Y){cnt=0;int l=0,cnt=0,g=0,B=X/Y;For(i,1,Y)E[i].clear();while(!S.empty()){++l;int x=S.top();S.pop();if((l-1)/B+1!=cnt)++cnt;if(cnt<=Y)E[cnt].push_back(x);else{++g;E[g].push_back(x);}}For(i,1,Y)solve(i);h=ask(a,b);For(i,1,Y){int x=get(i);S.push(x);}}int work(){while(!S.empty())S.pop();_For(i,0,n-1)S.push(i);For(i,1,8){a.clear(),b.clear();get(p[i-1],p[i]);}return S.top();}
};
int richest(int N,int T,int S){n=N;if(n<=1000)return Sub1::work();elsereturn Sub2::work();
}
![P10786 [NOI2024] 百万富翁](https://img2024.cnblogs.com/blog/3204443/202408/3204443-20240828224024278-1423842106.png) 讲解 P10786 [NOI2024] 百万富翁。先爆搜出 t>=9 的部分分,然后考虑使用动态规划算法进行常数优化跑出答案。
讲解 P10786 [NOI2024] 百万富翁。先爆搜出 t>=9 的部分分,然后考虑使用动态规划算法进行常数优化跑出答案。