Lecture 03 Real-time Shadows 1

news/2024/11/16 8:13:23/文章来源:https://www.cnblogs.com/Tellulu/p/18391221

Real-time Shadows 1

Recap: shadow mapping

Shadow Mapping

2-Pass Algorithm
- The light pass generates the shadow map
- the camera pass uses the shadow map
An image-space algorithm
- 好处：无需场景中的几何信息
- 坏处：导致自遮挡和走样问题

Pass

Pass 1: Render from light
- 从光源输出深度图
Pass 2: Render from Eye
- 从相机出发渲染
- 将实际相机看到的像素投影回光源看到的深度图（逆变换）记录的像素上，如果该点深度与光源记录的深度图中对应像素深度一致，则说明是同一个点，可以被看到，否则说明这个点是光源看不到的点，说明在阴影中
  
  使用Z值或者离相机的实际距离都可以，但两次Pass要比较同一种值

Shadow Mapping中的问题

Self occlusion 自遮挡

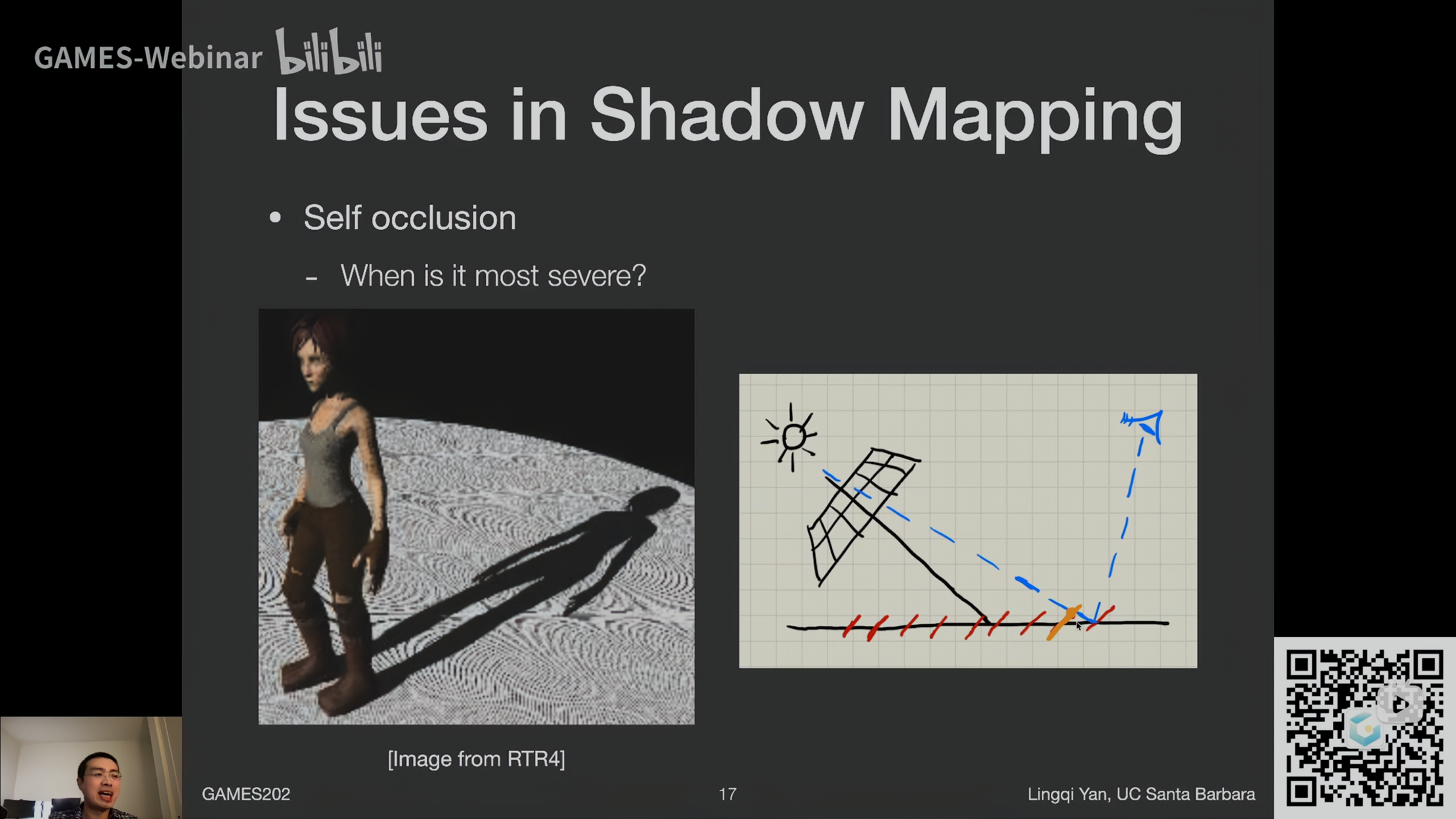
解决方法：
- 增加一个bias减轻自遮挡
  
  bias过大，出现Peter Pan现象(detached shadow)
  
  工业界几乎没有方法解决，只能找一个比较合适的bias
- Second-depth shadow mapping
  - Shadow Map中存最小深度和第二小深度
  - 使用最小深度和最二小深度的中值来做后续阴影比较
  - 这样无需设定bias（相当于自适应bias）
  - 工业界用的少
    
    原因：
    - 要求所有物体是watertight，即必须有正面反面，就算是一张纸，也得是很薄的一个物体
      
      比如说“地板”不是一个watertight（解决方法，记录次浅深度为无限大）
    - 输入的fragment是无序的，要始终保持最小和次小，要涉及到Swap，虽然时间复杂度仍然是\(O(n)\)，能够实现，但是实时渲染不相信复杂度，只相信绝对的速度，因为实时渲染要求速度很苛刻，\(n\)和\(2n\)差异很大

Aliasing 走样

The math behind shadow mapping

微积分中的不等式

Schwaz施瓦茨不等式

\[[\int_a^bf(x)g(x)dx]^2\le\int_a^bf^2(x)dx\cdot\int_a^bg^2(x)dx \]
Minkowski明可夫斯基不等式

\[\{\int_a^b[f(x)+g(x)]^2dx\}^{\frac{1}{2}} \le \{\int_a^b f^2(x)dx\}^{\frac{1}{2}} + \{\int_a^b g^2(x)dx\}^{\frac{1}{2}} \]

实时渲染中的重要约等式

\[\int_{\Omega}f(x)g(x)dx \approx \frac{\int_{\Omega}f(x)dx}{\int_{\Omega}dx} \cdot \int_{\Omega}g(x)dx \]

这里将两个乘积的积分转化成了两个积分的乘积，右侧分母\(\int_{\Omega}dx（=\int_{\Omega}1dx）\)是归一化常数

以下条件满足任一可认为约等式成立

Small support（当积分域很小时）
- point/directional lighting
  
  点光源或方向光时，只有一个点有光照
Smooth integrand，g(x)在积分域内比较光滑
- (diffuse bsdf / constant radiance area lighting)
  
  如有一个面光源，面光源内部给出radiance不变，这样L就完完全全smooth了
  
  在BRDF中，当BRDF是diffuse时，认为其变化非常小，当是glosssing，则不行
即使两项都不满足，也能强行用，如Ambient Occultation环境光遮蔽中

在Shadow Mapping中

\[L_o(p,\omega_o)=\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_iV(p,\omega_i)d\omega_i\\ 通过上面的约等式，可以转化成\\ L_0(p,\omega_o) \approx \frac{\int_{\Omega^+}V(p,\omega_i)d\omega_i}{\int_{\Omega^+d\omega_i}}\cdot\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_id\omega_i\\ 左式是Visibility(上式的V)，右式是shading，这样就把shading和visibility分开了 \]

于是在BRDF中，对于面光源或环境光照（环境光照可以理解为一个超大的面光源），Shadow Mapping是不准的

Percentage closer soft shadows (PCSS)

Soft shadows 软阴影：本影到没有阴影处的过渡

Percentage Closer Filtering (PCF)

PCF最早用于反走样（抗锯齿）

PCF的两点注意

不是对最后已经有阴影的地方进行Filter
如果是对Shadow Map做模糊，那阴影处和阴影外之间模糊的一圈毫无物理意义，且第二趟Pass和模糊了的Shadow Map做深度测试，得到的结果还是非0即1

PCF的工作原理：

普通Shadow Map是比较shading point变换到Shadow Map上对应点的深度，而PCF比较对应点周围一圈的深度（比如说\(7\times 7\)），将做完比较的结果平均（每次比较结果非0即1），得到一个visibility

PCF Filter的是任意一个shading point，做很多次阴影比较的结果

Filter size:

Filter size越大阴影越软。越小阴影越硬，那么是否各个不同的位置都要给一个相同大小的Filter size呢？

如图这里笔尖阴影非常锐利，几乎没有软阴影，而远处的阴影有软阴影

远近取决于shading point离投射阴影的point的距离（与遮挡物距离有关，与光源距离无关）

关键结论

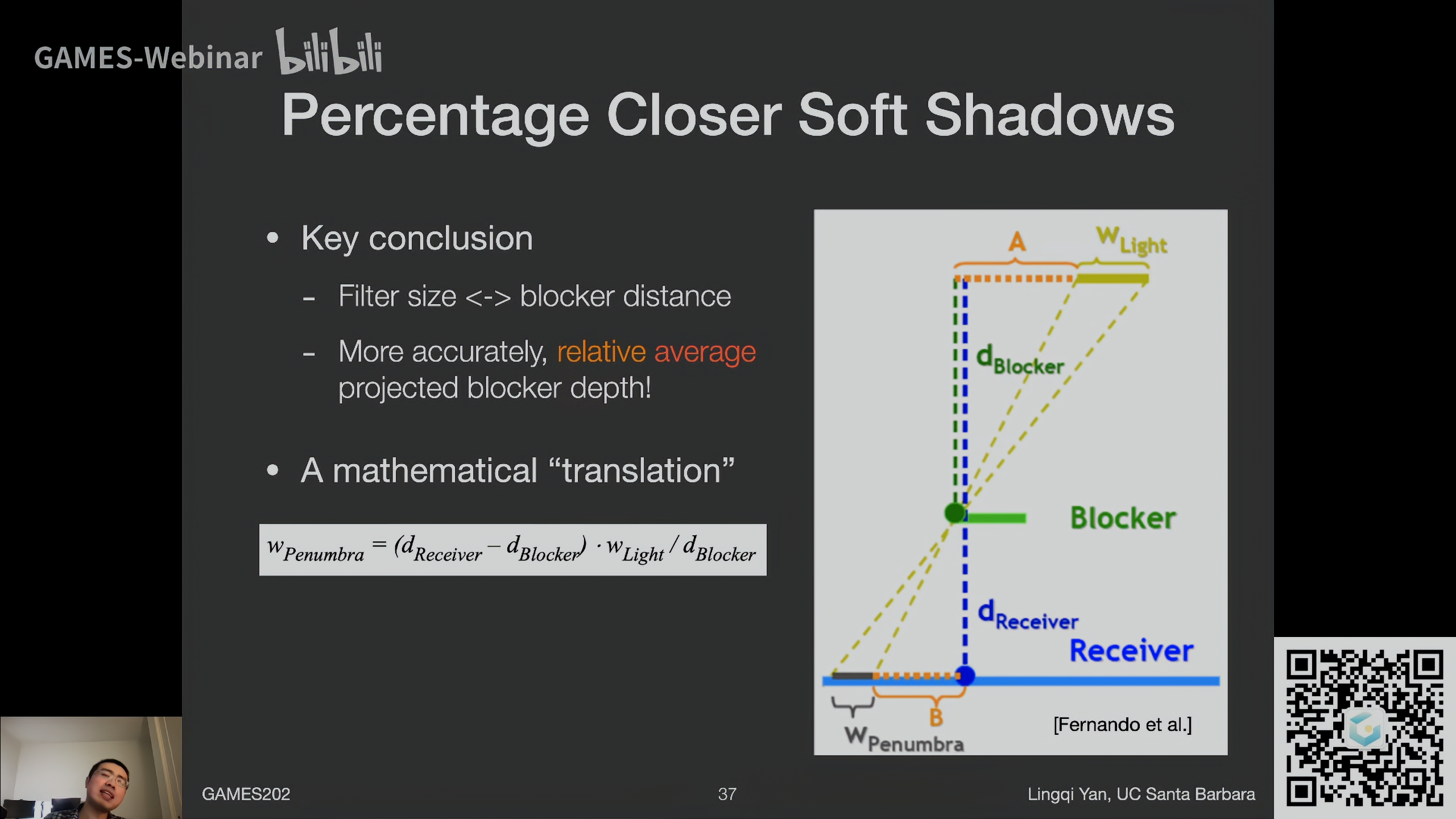
Filter size取决于遮挡物距离，更精确的说，与投射阴影的遮挡物的平均深度有关

根据相似三角形，可以得到半影范围与遮挡物距离的关系\(w_{Penumbra}=(d_{Receiver}-d_{Blocker})\cdot w_{Light}/d_{Blocker}\)，这里\(w_{Penumbra}\)一定程度就可以表示阴影软的程度

*对于面光源，原本是无法生成Shadow Map的，一般做法是将其当成点光源处理，将相机放在面光源中心生成Shadow Map

PCSS

step 1: Blocker search

在特定范围内获得average blocker depth

取周围区域，判断在不在阴影里，将所有Blocker的深度取平均记录（不是Blocker不管）
step 2: Penumbra estimation

使用average blocker depth确定filter size

知道各处filter size多大，后续就跟PCF做法一样了
step 3: Pencertage Closer Filtering

要获得average blocker depth时，需确定在多大范围内比较