GNN-RAG:以RAG形式将 llm 的语言能力与 gnns 推理进行联合

Paper: https://arxiv.org/abs/2405.20139

知识图(KGs)以三元组(头、关系、尾)的形式表示人类精心制作的事实知识，它们

共同构成了一个图。大型语言模型(Large Language Models, llm)是 QA 任务中最

先进的模型，因为它们具有理解自然语言的卓越能力。另一方面，图神经网络

(Graph Neural Networks, gnn)由于能够处理存储在 KG 中的复杂图信息而被广

泛应用于 KGQA。

在本文[1]中，作者介绍了 GNN-RAG，这是一种以检索-增强生成(RAG)风格将

llm 的语言理解能力与 gnn 的推理能力相结合的新方法。

主要贡献:

• 框架:GNN-RAG 将 gnn 重新用于 KGQA 检索，以增强 llm 的推理能力。

• 有效性和可靠性:GNN-RAG 在两个广泛使用的 KGQA 基准(WebQSP 和

CWQ)中实现了最先进的性能。

• 效率:GNN-RAG 提高了 KGQA 性能上的普通 llm，而不会像 KGQA 的现

有 RAG 系统那样需要额外的 LLM 调用

问题陈述和背景

i) KGQA

• 给定一个 KG G，它包含的事实表示为(v, r, v ')，其中 v 表示头部实体，v '

表示尾部实体，r 是两个实体之间的对应关系。

• 给定 G 和一个自然语言问题 q, KGQA 的任务是提取一组正确回答 q 的实

体{a}∈G

ii)检索与推理(Retrieval & Reasoning)

• 由于 KGs 通常包含数百万个事实和节点，因此为问题 q 检索较小的特定

于问题的子图 Gq，例如，通过实体链接和邻居提取。

iii) gnn 网络

• KGQA 可以看作是一个节点分类问题，其中 KG 实体被分类为给定问题的

答案和非答案

iv)llm

• 用于 KGQA 的 llm 使用 KG 信息执行检索增强生成(RAG)，如下所示。

• 首先将检索到的子图转换为自然语言，以便 LLM 对其进行处理。

• 给llm的输入包含 KG 事实信息以及问题和提示

v)基于llm的寻回器

• 作者提出了一个基于llm的检索器(RoG;[4])。

• 给定训练问题-答案对，RoG 从问题实体开始提取到答案的最短路径，以

便对检索器进行微调。

• 基于提取的路径，对 LLM(LLaMA2-Chat-7B [Touvron et al.， 2023])进

行微调，以生成给定问题 q 为 LLM(prompt, q) =⇒{r1→···→rt}k 的推理

路径，

GNN-RAG

i)工作流程

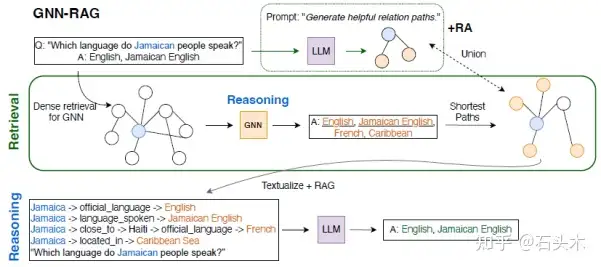
GNN-RAG 的工作流程如下:

• 首先，GNN 在密集 KG 子图上进行推理，以检索给定问题的候选答案。

• 其次，提取 KG 中连接问题实体和基于 gnn 的答案的最短路径，以表示有

用的 KG 推理路径。提取的路径被语言化，并作为使用 RAG 进行 LLM 推理

的输入。

• GNN 作为密集子图推理器来提取有用的图信息，而 LLM 则利用其自然语

言处理能力来实现最终的 KGQA

ii) GNN

• gnn 被用于检索，因为它们具有探索多种推理路径的架构优势，从而导致

高答案召回率。

• 当 GNN 推理完成后，根据其最终 GNN 表示 h(L) v 对子图中的所有节点

进行答案与非答案评分，然后进行 softmax(·)操作

• 使用训练问题-答案对通过节点分类(答案与非答案)对 GNN 参数进行优化。

在推理过程中，具有最高概率分数的节点(例如，高于概率阈值)作为候选答案

返回，以及连接问题实体与候选答案的最短路径(推理路径)。

• 检索到的推理路径被用作基于 llm 的 RAG 的输入

3) LLM

• 在通过 GNN-RAG 获得推理路径后，我们将其语言化，并将其作为输入给

下游的 LLM，如 ChatGPT 或 LLaMA。然而，llm对输入提示模板和图

形信息的语言表达方式很敏感

• 为了解决这个问题，RAG 提示调优[2][3]用于具有开放权值且可训练的llm

• LLaMA2-Chat-7B 模型基于训练的问答对进行微调，生成正确答案列表，

给出提示:“基于推理路径，请回答给定的问题。”\n 推理路径:{推理路径}\n

问题:{问题}"。

• 推理路径表述为“{问题实体}→{关系}→{实体}→···→{关系}→{答

案实体}\n”，GNN-RAG 如上图所示

iv)检索分析:为什么 gnn 及其局限性

gnn 利用图结构来检索包含多跳信息的 KG 的相关部分。

• 作者训练了两个不同的 GNNs，一个深 gnn (L = 3)和一个浅 gnn (L = 1)，

并测量了它们的检索能力

• 报告了“答案覆盖率”指标，它评估检索器是否能够为 RAG 获取至少一

个正确答案

• 下表显示了 WebQSP 数据集的单跳和多跳问题与基于 llm 的检索器的

GNN 检索结果，其中“#Input Tokens”表示检索到的 KG 路径的输入令牌

的中位数

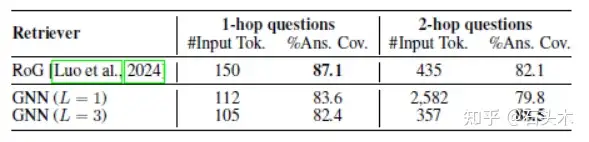
• 结果表明，深度 GNNs (L = 3)可以更有效地处理复杂的图结构并检索有用

的多跳信息(%Ans)。Cov.)和高效(#Input Tok.)比 LLM 和浅 GNN。

• 另一方面，GNNs 的局限性是针对简单的(1 跳)问题，其中准确的问题关系

匹配比深度图搜索更重要

v)检索增强(RA)

• 检索增强(RA)将从不同方法检索到的 KG 信息组合在一起

• 作者提出了一种 RA 技术(GNN-RAG +RA)，它将 GNN 寻回器与基于 llm

的寻回器相补充，分别结合了它们在多跳和单跳问题上的优势。以增加多样

性和答案召回率

• 基于 llm 的检索的一个缺点是，它需要多代(波束搜索解码)来检索不同的

路径，这是以效率换取有效性

• 一个更便宜的替代方案是通过组合不同GNNs的输出来执行RA，这些gnn

配备了不同的 lm

• GNN-RAG+Ensemble 采 用 两 个 不 同 GNN (GNN+SBERT 和

GNN+LMSR)检索路径的并集作为 RAG 的输入

实验结果

i)主要结果

• 下表给出了不同 KGQA 方法的性能结果

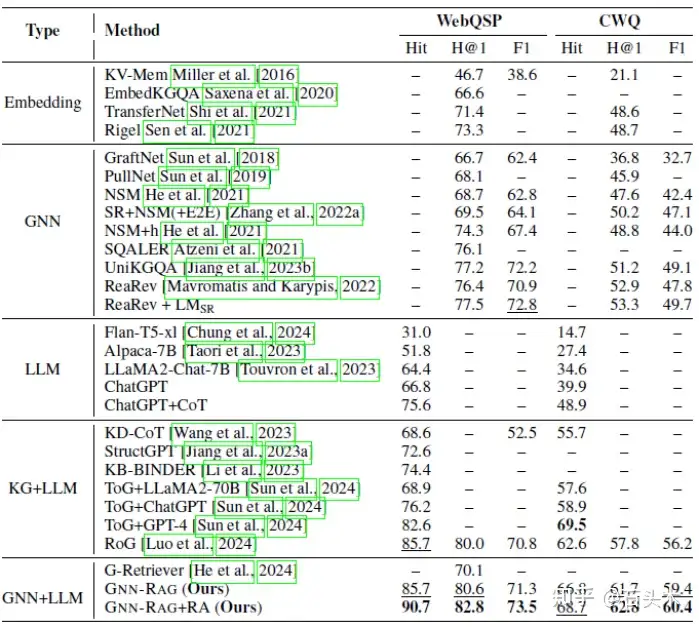
• 上面的结果表明，GNN-RAG 总体上表现最好，在几乎所有指标的两个

KGQA 基准测试中都取得了最先进的结果

• 结果表明，为 LLM 配备基于 GNN 的检索可以显著提高其推理能力

(GNN+LLM vs. KG+LLM)。

• GNN-RAG+RA 在 Hit 上的性能优于 RoG 5.0-6.1%，而使用只有 7B 参数

的 LLM 和更少的 LLM 调用时，它的性能优于或匹配 ToG+GPT-4

• GNN-RAG +RA 在 Hit 中比 ToG+ChatGPT 高出 14.5%，在 Hits@1 和 F1

中表现最好的 GNN 分别高出 5.3-9.5%和 0.7-10.7%。

ii)多跳和多实体 KGQA

• 下表比较了多跳问题(答案距离问题实体不止一跳)和多实体问题(具有多

个问题实体)的性能结果

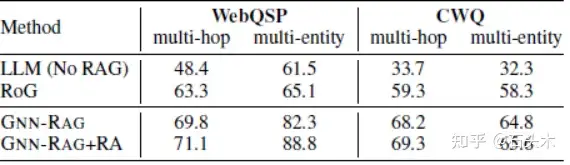
• GNN-RAG 利用 gnn 处理复杂的图形信息，在 WebQSP 上比 RoG(基于

LLM-based 的检索)在 F1 上高出 6.5-17.2%，在 CWQ 上比前者高出 8.5-8.9%

• GNN-RAG+RA 在 F1 上提供了高达 6.5%的额外改进，这表明当深度图搜

索对于成功的 KGQA 很重要时，GNN-RAG 是一种有效的检索方法。

iii)检索增强

• 下表比较了 GNN-RAG 的不同检索增强

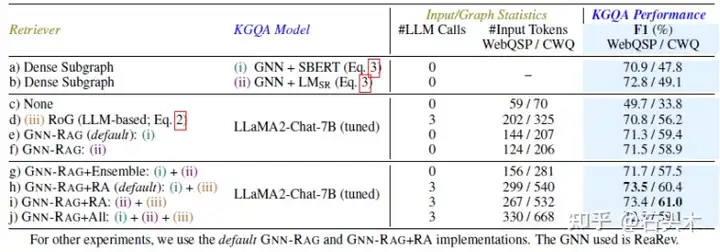
• 以上结果表明，基于 gnn 的检索比基于 LLM 的检索更高效(#LLM Calls，

#输入令牌)和有效(F1)，特别是对于复杂问题(CWQ)。

• 当结合 gnn 诱导的推理路径和 llm 诱导的推理路径时，检索增强效果最好

(F1)，因为它们获取非重叠的 KG 信息(增加的#输入令牌)，从而提高了 KGQA

的检索

• 增加所有检索方法不一定会提高性能(F1)，因为长输入(#输入令牌)可能会

混淆 LLM

• 虽然两种gnn在KGQA (F1)上的表现不同，但它们都能通过llm改善RAG，

然而，弱 gnn 并不是有效的检索器

iv)对 llm 的检索效果

• 下表给出了使用GNN-RAG或LLM-based检索器(RoG和ToG)的各种llm

的性能结果。

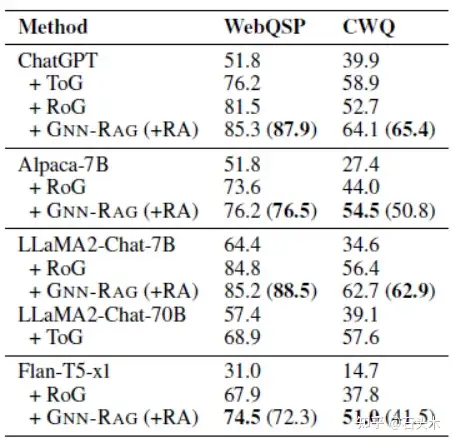
• 作者报告 Hit 指标，因为很难从 LLM 的输出中提取答案的数量。

• GNN-RAG (+RA)是对 RAG 改进最大的检索方法

• GNN-RAG 显著提高了弱 LLMs(如 Alpaca-7B 和 Flan-T5-xl)的 KGQA 性

能。与 RoG 相比，Hit 的改进高达 13.2%，而 GNN-RAG 使用轻量级的 7B

LLaMA2 模型优于 LLaMA2- chat - 70b +ToG。

v)关于忠实度的案例研究

• 下面的两个案例研究说明了 GNN-RAG 如何提高 LLM 的可靠性。在这两

种情况下，GNN-RAG 检索回答复杂问题所必需的多跳信息。

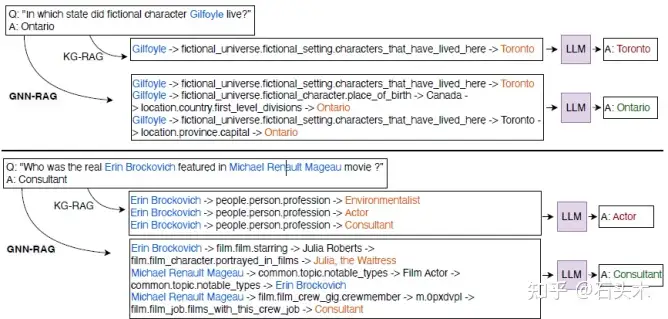
• 下面的案例研究说明了检索增强(RA)的好处。RA 使用 LLMs 来获取语义

相关的 KG 信息，这些信息可能被 GNN 遗漏了

1.GNN-RAG: Graph Neural Retrieval for Large Language Model Reasoning by Mavromatis et

al.arXiv:2405.20139

2.Ra-dit: Retrieval-augmented dual instruction tuning. by Lin et al.arXiv preprint

arXiv:2310.01352, 2023

3.Graph chain-of-thought: Augmenting large language models by reasoning on graphs. by

Zhang et al. arXiv preprint arXiv:2404.07103, 2024

4.Reasoning on graphs: Faithful and interpretable large language model reasoning. by

Luo et al. In International Conference on Learning Representations,