代码随想录day50 || 图论基础

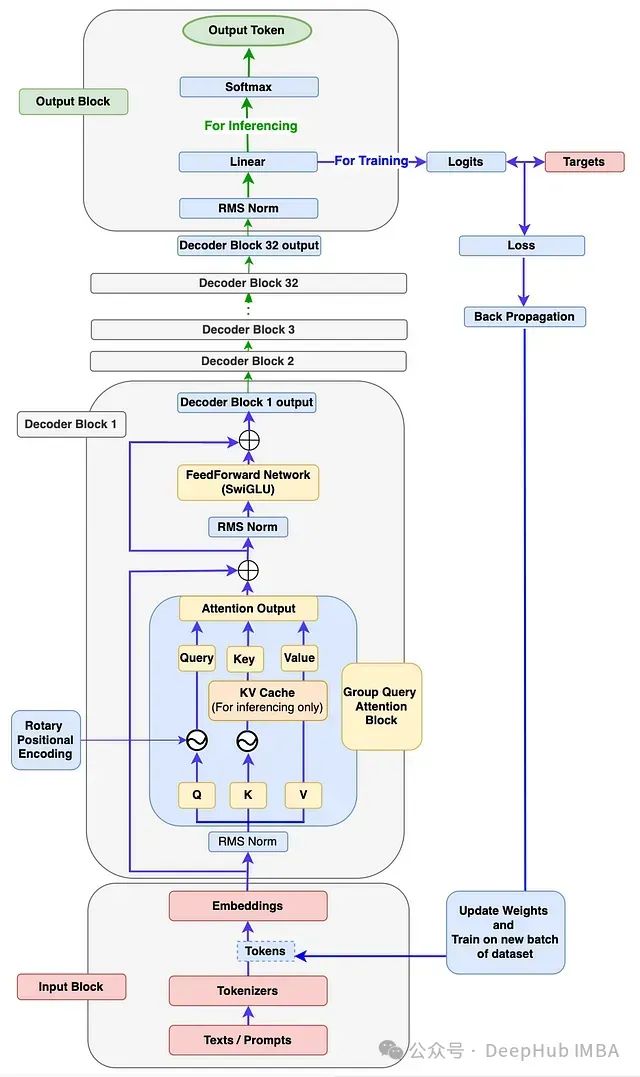
图论

基础定义

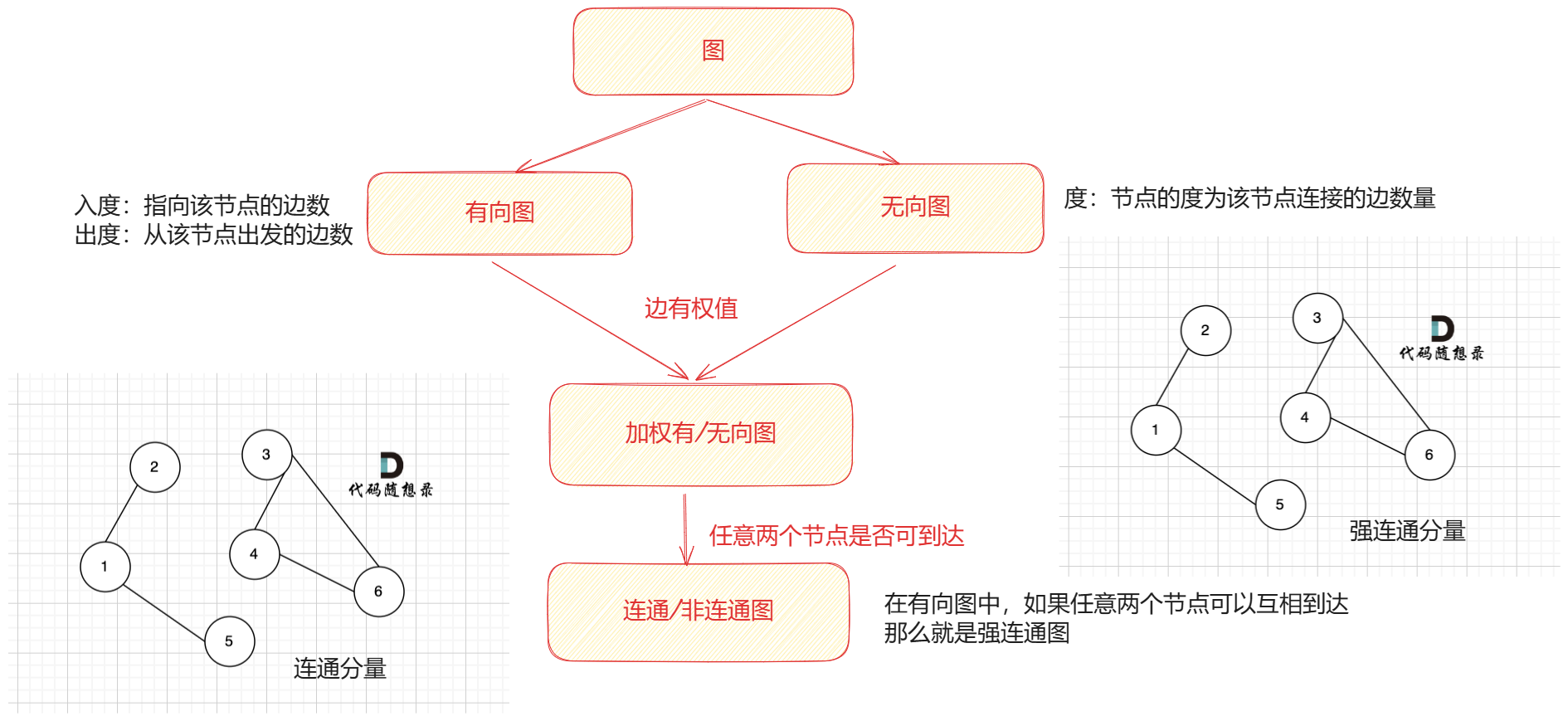
图的构造方式

1，邻接矩阵

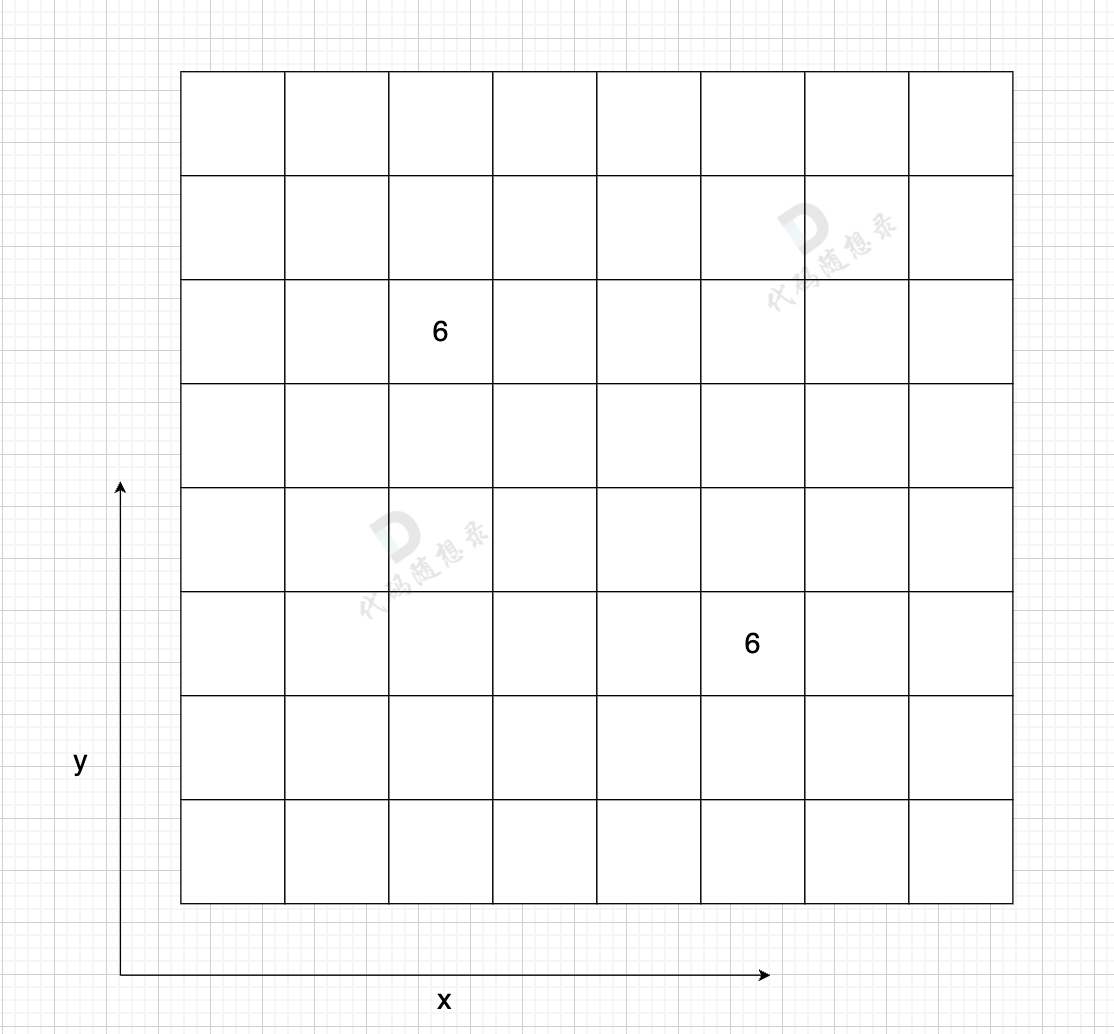
矩阵位置array[i][j] = k, i表示节点i，j表示节点j，[i][j] 表示i-->j存在一条边，k表示的是边的权重邻接矩阵的优点：
表达方式简单，易于理解
检查任意两个顶点间是否存在边的操作非常快
适合稠密图，在边数接近顶点数平方的图中，邻接矩阵是一种空间效率较高的表示方法。缺点：
遇到稀疏图，会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵，造成时间浪费

2，邻接表

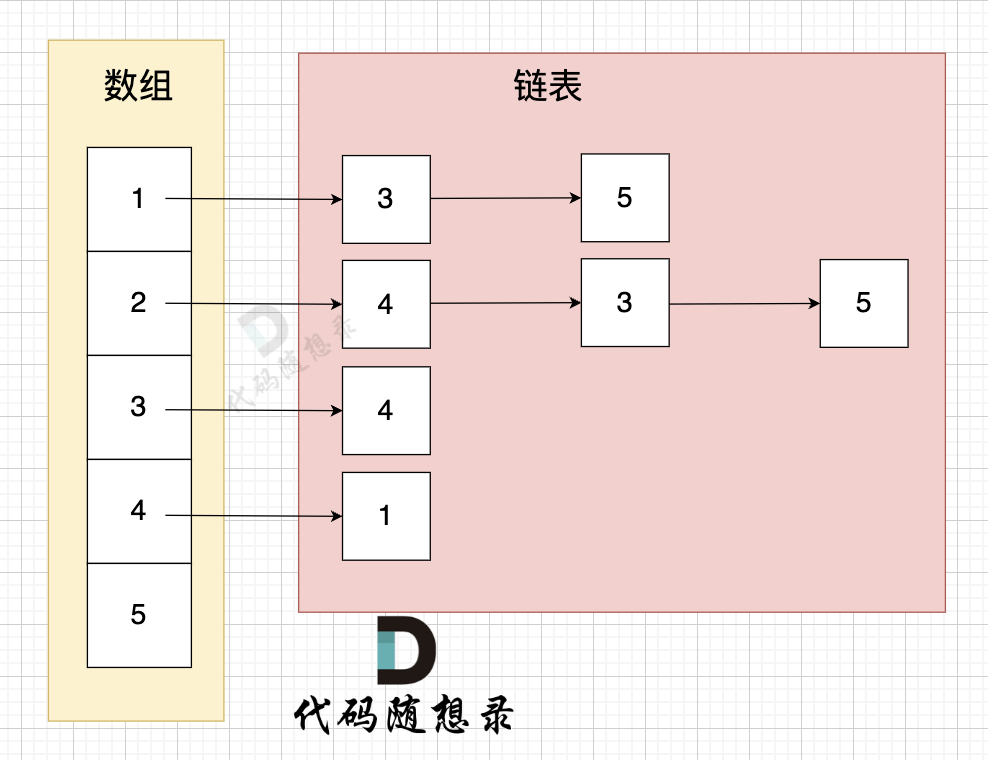
邻接表的数组存放的所有节点，每个位置对应的链表保存了该节点的所有度，eg: 1-->3-->5 代表节点1分别指向了节点3 和 节点5邻接表的优点：
对于稀疏图的存储，只需要存储边，空间利用率高
遍历节点连接情况相对容易缺点：
检查任意两个节点间是否存在边，效率相对低，需要 O(V)时间，V表示某节点连接其他节点的数量。
实现相对复杂，不易理解

797 图所有路径

var path []int
var res [][]intfunc allPathsSourceTarget(graph [][]int) [][]int {// 本体是一个有向图，参数已经给出了邻接表的结构// 本题是搜索路径，先考虑dfs，深度优先，原理是先一条路走到头，然后回溯，走下一条路path = []int{0}res = [][]int{}dfs(graph, graph[0], len(graph)-1)return res
}func dfs(graph [][]int, route []int, target int) {  // 回溯参数返回值// 回溯终止条件 + 收集结果if path[len(path) - 1] == target{var copypath = make([]int, len(path))copy(copypath, path)res = append(res, copypath)return}if len(route) == 0{return}// for{单次回溯逻辑}for i:=0; i<len(route); i++ {path = append(path, route[i])dfs(graph, graph[route[i]], target)path = path[ : len(path) - 1]}return
}