洛谷 P5658 [CSP-S2019] 括号树
题意
给定一棵树,每个点有一个括号 ( 或 )。
定义 \(s_i\) 表示 根节点到 \(i\) 每个点的括号组成的序列。
求每个 \(s_i\) 中合法括号子串的个数 \(f_i\)。
思路
定义 \(g_i\) 表示 \(s_i\) 中以 \(i\) 结尾的合法括号子串的个数。
有 \(f_i=f_{fa_i}+g_i\),求出 \(g_i\) 即可。
若 \(i\) 为左括号,\(g_i=0\)。
若 \(i\) 为右括号,
若没有左括号和它匹配,\(g_i=0\),
若有左括号和它匹配,设为第 \(j\) 个,\(g_i=g_{fa_j}+1\)。
即这一段匹配的括号接在上一段后面,又多出来了一个。
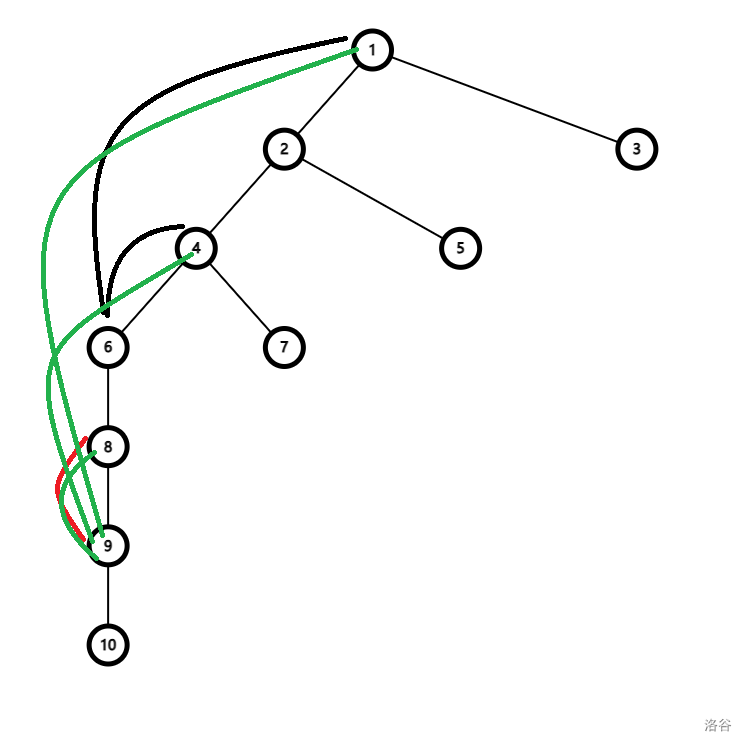
如图,黑色表示上一段的 \(g\),红色表示这一段匹配的括号,绿色表示这一段的 \(g\)。
由于两个合法子串拼接后仍为合法子串,所以 \([8,9]\) 可以单独,也可以和 \([6,4],[6,1]\) 拼接,这样就是 \(g_6+1\)。
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 5e5 + 5;
int n, fa[N], stk[N], top;
char s[N];
ll ans, g[N], f[N];
vector <int> E[N];
void dfs(int x) {int flg = 0;if (s[x] == '(') stk[++ top] = x;else if (top) g[x] = g[fa[stk[top]]] + 1, flg = stk[top --]; f[x] = f[fa[x]] + g[x];for (auto y : E[x]) dfs(y);if (s[x] == '(') top --;else if (flg) stk[++ top] = flg;
}
int main() {scanf("%d", &n);scanf("%s", s + 1);for (int i = 2; i <= n; i ++) scanf("%d", &fa[i]), E[fa[i]].push_back(i);dfs(1);for (int i = 1; i <= n; i ++) ans ^= 1ll * i * f[i];printf("%lld\n", ans);return 0;
}