本文是 Mamba 阅读第一篇文章,本来想从三个问题出发(1)不同 SSM 模型的区别是什么?(2)Transformer 和 SSM 可以等效吗?什么情况下可以等效?(3)很多实验表明 Mamba1 和 Mamba2 并不是单纯替代关系[1],Mamba2 相比 Mamba1 的变化是什么?即 SSM 部分、Transformer 部分 以及 计算部分。时间有限后续博客完成遥遥无期,故将第一部分整理发表。
动态模型发展: 从 Transformer 到 Mamba
最近模型架构从静态计算到动态计算转变趋势越发明显,也许 Transformer 强大 scalability 来自其动态计算特征。
所谓静态计算,指参与计算的俩个操作数一个属于事先已知的静态参数(比如权重)一个属于推理中产生的动态参数(比如特征),传统 MLP 以及卷积层都属于静态计算;而动态计算则是俩个操作数都属于动态参数,比如早期动态卷积中的加权混合以及 Transformer 中的 Q、K 乘法等等。
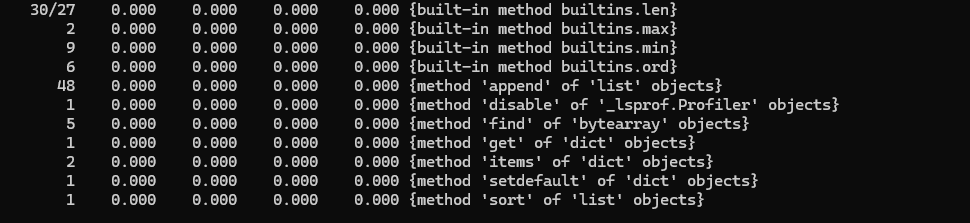
模型中加入动态计算使得计算需求并不能单一反映计算量。比如 Transformer 的 KV Cache 容量随着 Token 数量平方增长。动态计算需求和模型参数一起反映模型规模更加准确。
但 Transformer 随着 Token 数量增长动态开销太过巨大,如果将 KV Cache 看作过去输入带来的状态,那么 Transformer 就像无损压缩将所有信息存储。针对 Transformer 巨大的开销,Mamba 采用 SSM 中的状态变量压缩所有过去输入信息,并引入动态机制选择性压缩重要部分。
一言以蔽之,Mamba 是采用 State Space 压缩过去信息的动态模型。

如图,MoE 机制将模型容量和激活参数解耦,而动态机制将激活参数和硬件容量需求解耦。动态模型下以静态模型参数作为唯一衡量指标并不恰当。

本文接下来将对各种 SSM 模型总结,从 SSM 角度梳理 Mamba2 的模型发展。
说文解字,从 S4 到 SSD
按 Mamba2 文章中 SSM 模型分为 3 类:
- Structured State Space Model (传统卡尔曼现代控制理论中 S4 模型)
- Diagnoal State Space Model (包括 S4D、S6[2])
- Scalar-Identity SSM (也叫 1-Semiseparable Structed Masked Attention,包括 SSD)

S4 模型 4 个 S 来自 Structed State Space Sequential Model,也就是卡尔曼控制理论表示用状态方程和输出方程表示控制关系的那一套。其中 Sequential 揭示了 SSM 的计算本质,sequential 是有序 1D 数据结构,顺序性和 Transformer 中并行计算所有一个窗口内 Token 不同,而顺序 1D 与处理 2D 图像数据乃至 3D 空间数据相矛盾,后续 Mamba 扩展到非语言任务所采用五花八门的 trick 源自这里。

而将 SSM 迁移到 ML 中便是假设矩阵参数 A、B、C、D 是学习的权重参数,而输入作为激励 u,计算状态 x 和输出 y。实际推理是由于权重固定,实际对应的是 time-invariant 模型。

回到 SSM 的计算形式,时间维对应实际是 token 的数量,和实际推理有关是一个动态维度,除了动态维度每个变量还有些固定静态维度,比如输入维度 p、状态维度 n 和输出维度 q。计算上状态空间便是用 A、B、C、D 矩阵将数据在 p、n、q 维度之间互相投影变化。 基于模型扩展考虑,输入输出维度一般选择相同,即 p = q。

自然可知状态方程中 A 是 nxn 的方程,表示状态变量在时间维度的作用关系。若将 A 退化为对角矩阵,从 nxn 退化到 n 个自由参数,Ax 矩阵向量乘退化到俩个 n 维向量乘法,便是 Diagonal State Space Model。
但此时模型仍是静态模型,A、B、C、D 是静态参数,因此 SSM 的计算也是静态计算。前文说到 SSM 可以看作将历史信息压缩到固定大小的空间(状态变量),而对于时间维度上不变的 A、B、C、D 就像对任何时间压缩率相等,那么显而易见,随着输入序列长度变大,历史信息在固定空间中所占比例更小。对所有信息采用相同压缩率并不符合压缩的味道,而 time-invariant 也有现实时变系统更多概念相违背。
因此 Mamba 再加了一个 S:Selective,A、B、C、D 并不直接由模型权重提供,而是计算中类似 Q、K、V 动态生成,实际是将 SSM 变为 time-variant 系统。
S6 中的另一个 S 则有点特殊,并非是模型的变动而是类似 Flash Attention 具体计算执行上的变化。前文说到 SSM 一个重要特征是天然 sequential 特性,这个特征实际与并行加速存在冲突,因为有序性,后面的输出要等到前面的输出结果,这种依赖关系便限制了并行加速。更专业的术语叫做前缀和问题(prefix sum)或者扫描问题(scan)[3],前缀和问题想要并行加速必定要引入额外的计算量[4],但如何在资源开销增加和加速销量之间 trade-off 仍然是一个重要的问题。Mamba 中使用的是 Blelloch 提出的前缀和算法[5]。
可见 Mamba 有俩个明显的特征,一是理论延续性,SSM 家族的高贵血统使得系列工作中对数学的合理异常重视(当然一旦扯到Machine Learning解释性就靠边站了);二是不但对模型理论修正,计算实现也非常重视,毕竟是做出 Flash Attention 的作者呐。
那么进一步也不难猜测,Scalar-Idenetity 便是在 Diagnoal 基础上进一步退化 A,从n维向量直接退化到一个标量。
比如 Jamba 指出纯 Mamba 架构 Mamba2 胜过 Mamba1,但attn-Mamba 混合架构下 Mamba1 胜过 Mamba2 ,见 Jamba-1.5: Hybrid Transformer-Mamba Models at Scale ↩︎
Mamba 类模型从卡尔曼 State Space Model 发展而来,除了有按 DNN 这边起名传统的昵称(什么 ELMO、BERT、Transformer),也有能反映在 SSM 家族谱系的正式名称,比如 Mamba1 也叫 S6,Mamba2 也叫 SSD ↩︎
扫描这个词非常生动形象,很容易联想到老式显像管电子束来回扫描出影像的画面。更泛化地说,扫描是将空间的信息按某种顺序在时间维上挨个输入。 ↩︎
这里的计算量并非指增加计算单元。而是变化模型的计算量本身,举个例子,对于一个固定模型,其计算量是固定的,增加单元只是缩短计算时间,而这里是类似 Flash Attention 中为了使算法可迭代引入了额外的迭代计算步骤一样,增加了总体计算量。 ↩︎
Prefix Sums and Their Applications ↩︎


![洛谷 P5658 [CSP-S2019] 括号树](https://cdn.luogu.com.cn/upload/image_hosting/qm7ooxbi.png)