线段树分治

适用

某一个条件在查询的一段区间中存在的问题

如:有 \(t\) 个询问,每个询问输入一条边 \(u, v\), 如果当前图中没有这条边,那么插入这条边;反之删除这条边

思路

假设有 \(q\) 组询问,并且 \(q = 8\),我们就对 \(q\) 组询问建一棵线段树,如下图:

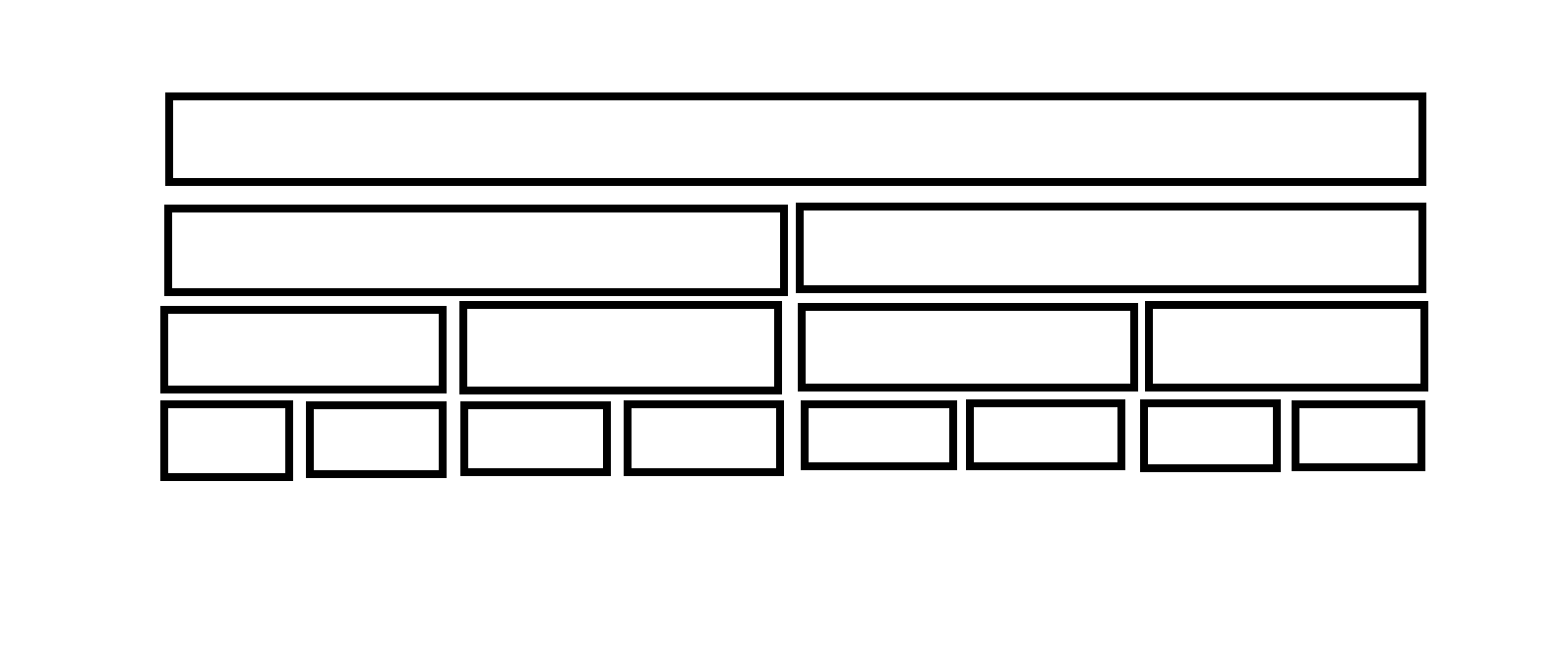
假设现在第一个条件出现在了 \(3\) 到 \(7\) 这个区间内,那么图将变成这样:

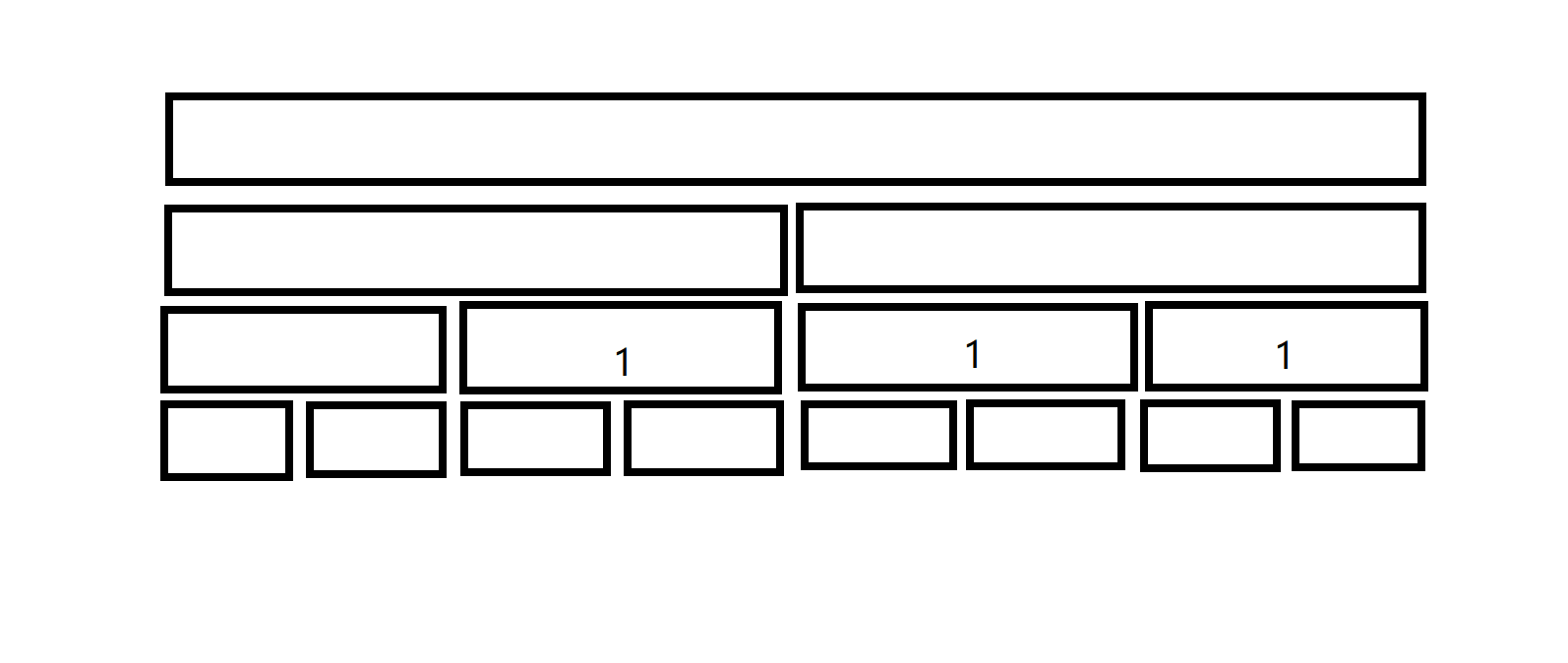
假设现在第二个条件出现在了 \(1\) 到 \(6\)这个区间内,那么图将变成这样:

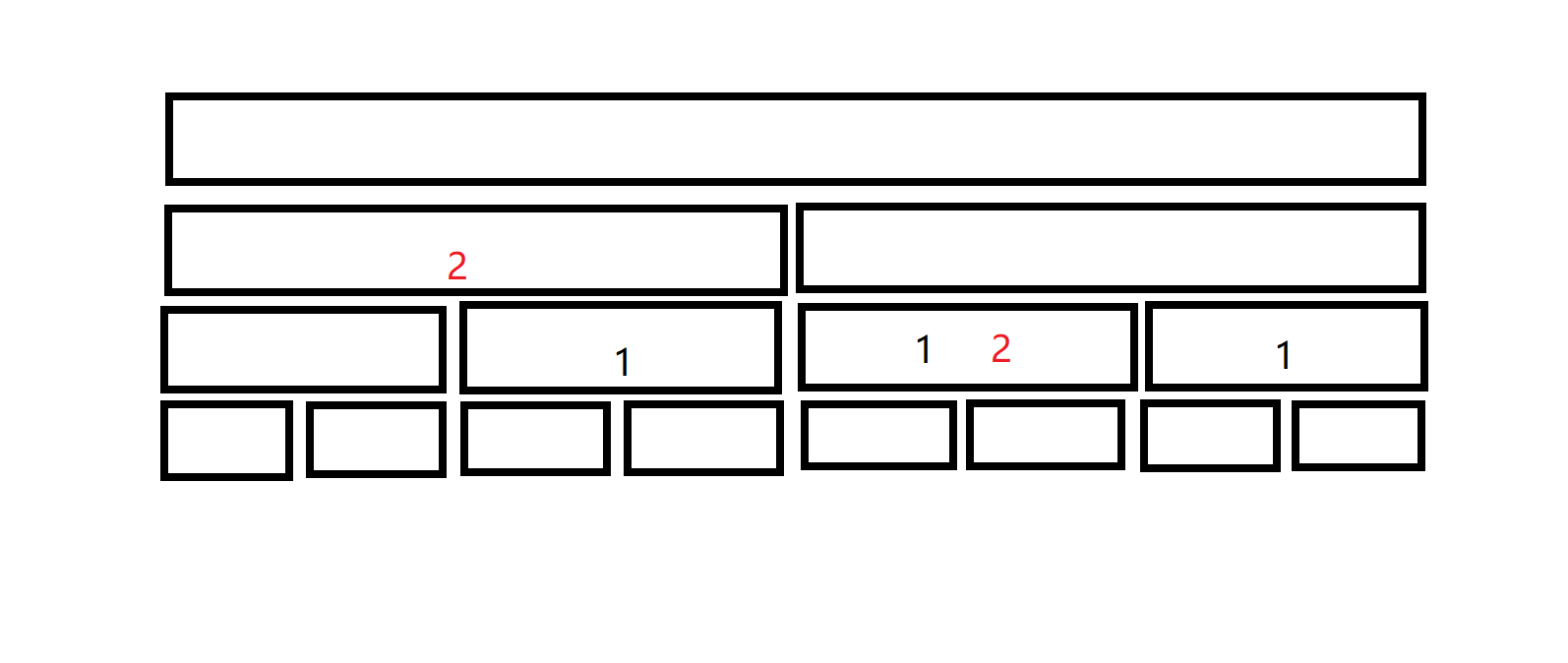
由于每个询问最多会打 \(log(q)\) 个标记,所以时间复杂度为 \(q \times log(q)\)

Connect and Disconnect

看到题面,我们肯定会想到用并查集维护,可是普通的并查集并不支持删除操作,可是支持撤销操作,所以我们要使用线段树分治
code:

#include <bits/stdc++.h>using namespace std;const int N = 3e5 + 5;int n, k, u[N], v[N], len[N], ans, sz[N], fa[N];bool vis[N];char op[N];map<pair<int, int>, int > mp;vector<int> tr[N * 4];vector<pair<int, int> > stk;int find(int x) {if (fa[x] == x) {return x;}return find(fa[x]);
}bool merge(int x, int y) {x = find(x), y = find(y);if (x == y) {return 0;}if (sz[x] > sz[y]) {swap(x, y);}fa[x] = y;sz[y] += sz[x];stk.push_back({x, y});//记录合并了哪些return true;
}void cancel() {//撤销auto [x, y] = stk.back();stk.pop_back();sz[y] -= sz[x];fa[x] = x;
}void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {int tot = 0;for (auto cur : tr[i]) {tot += merge(u[cur], v[cur]);}ans -= tot;if (l == r) {if (vis[l]) {cout << ans << "\n";}}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}ans += tot;while (tot--) {cancel();}
}int main() {ios::sync_with_stdio(0);cin.tie(0);freopen("connect.in", "r", stdin);freopen("connect.out", "w", stdout);cin >> n >> k;if (k == 0) {return 0;}for (int i = 1; i <= k; i++) {cin >> op[i];if (op[i] == '-') {cin >> u[i] >> v[i];if (u[i] > v[i]) {swap(u[i], v[i]);}len[mp[{u[i], v[i]}]] = i - mp[{u[i], v[i]}] + 1;}else if (op[i] == '+') {cin >> u[i] >> v[i];if (u[i] > v[i]) {swap(u[i], v[i]);}mp[{u[i], v[i]}] = i;}else vis[i] = true;}for (int i = 1; i <= k; i++) {if (u[i] && v[i] && !len[i] && op[i] == '+') {len[i] = k - i + 1;}//求出区间}for (int i = 1; i <= k; i++) {if (!len[i]) {continue;}modify(1, 1, k, i, i + len[i] - 1, i);}for (int i = 1; i <= n; i++) {fa[i] = i;sz[i] = 1;}ans = n;query(1, 1, k);return 0;
}

Disconnected Graph

由于不能直接从图中删去边,所以还是要用线段树分治
code:

#include <bits/stdc++.h>using namespace std;const int N = 1e6 + 2e5 + 5;int n, m, k, u[N], v[N], ans, sz[N], fa[N];vector<int> tr[N * 4], tmp[N];vector<pair<int, int> > stk;int find(int x) {if (fa[x] == x) {return x;}return find(fa[x]);
}bool merge(int x, int y) {x = find(x), y = find(y);if (x == y) {return 0;}if (sz[x] > sz[y]) {swap(x, y);}fa[x] = y;sz[y] += sz[x];stk.push_back({x, y});return true;
}void cancel() {auto [x, y] = stk.back();stk.pop_back();sz[y] -= sz[x];fa[x] = x;
}void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {int tot = 0;for (auto cur : tr[i]) {tot += merge(u[cur], v[cur]);}ans -= tot;if (l == r) {if (ans == 1) {cout << "Connected\n";}else cout << "Disconnected\n";}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}ans += tot;while (tot--) {cancel();}
}int main() {ios::sync_with_stdio(0);cin.tie(0);freopen("disconnected.in", "r", stdin);freopen("disconnected.out", "w", stdout);cin >> n >> m;for (int i = 1; i <= n; i++) {fa[i] = i;sz[i] = 1;}ans = n;for (int i = 1; i <= m; i++) {cin >> u[i] >> v[i];}cin >> k;for (int i = 1, cnt, a; i <= k; i++) {cin >> cnt;for (int j = 1; j <= cnt; j++) {cin >> a;tmp[a].push_back(i);}}for (int i = 1; i <= m; i++) {if (!tmp[i].size()) {modify(1, 1, k, 1, k, i);continue;}if (tmp[i][0] != 1) {modify(1, 1, k, 1, tmp[i][0] - 1, i);}for (int j = 1; j < tmp[i].size(); j++) {if (tmp[i][j - 1] + 1 != tmp[i][j]) {modify(1, 1, k, tmp[i][j - 1] + 1, tmp[i][j] - 1, i);}}if (tmp[i][tmp[i].size() - 1] != k) {modify(1, 1, k, tmp[i][tmp[i].size() - 1] + 1, k, i);}}query(1, 1, k);return 0;
}

二分图 /【模板】线段树分治

都不用分析就能看出来是线段树分治,只不过要维护是否为二分图

如何维护是否为二分图呢?

分为两个集合,编号 \(1\) 至 \(n\) 表示为二分图的左边,编号 \(n + 1\) 至 \(2 \times n\) 表示为二分图的右边 (左右不重要),那么对于一条边 \(u, v\), 我们就要将 \(u\) 与 \(v + n\) 建边,将 \(u + n\) 与 \(v\) 建边,如果有一个点 \(x\) 使得 \(x\) 与 \(x + n\) 在同一个集合里,自然就不是二分图
code:

#include <bits/stdc++.h>using namespace std;const int N = 5e5 + 5;int n, m, k, u[N], v[N], ans, sz[N], fa[N];//ans记录有几个不符合要求的bool vis[N];vector<int> tr[N * 2], tmp[N];vector<pair<int, int> > stk;int find(int x) {if (fa[x] == x) {return x;}return find(fa[x]);
}bool merge(int x, int y) {x = find(x), y = find(y);if (x == y) {return 0;}if (sz[x] > sz[y]) {swap(x, y);}fa[x] = y;sz[y] += sz[x];stk.push_back({x, y});if (!vis[x] && find(x + n) == find(x)) {ans++;vis[x] = true;}if (!vis[y] && find(y + n) == find(y)) {ans++;vis[y] = true;}return true;
}void cancel() {auto [x, y] = stk.back();stk.pop_back();sz[y] -= sz[x];fa[x] = x;if (vis[x] && find(x + n) != find(x)) {ans--;vis[x] = false;}if (vis[y] && find(y + n) != find(y)) {ans--;vis[y] = false;}
}void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {int tot = 0;for (auto cur : tr[i]) {tot += merge(u[cur] + n, v[cur]);tot += merge(u[cur], v[cur] + n);}if (l == r) {if (l != k) {if (ans == 0) {cout << "Yes\n";}else cout << "No\n";}}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}while (tot--) {cancel();}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m >> k;k++;for (int i = 1; i <= 2 * n; i++) {fa[i] = i;sz[i] = 1;}for (int i = 1, l, r; i <= m; i++) {cin >> u[i] >> v[i] >> l >> r;if (l == r) {continue;}l++;modify(1, 1, k, l, r, i);}query(1, 1, k);return 0;
}

大融合

简化题面后其实就是对于要询问的这条边 \(u, v\) 求出将 \(u, v\) 断开后, \(u\) 集合内的元素数量乘 \(v\) 集合里的元素数量

如何确定一条边出现的区间

如果是第 \(x\) 条边,那么出现区间为 \([1, x - 1]\) 与 \([x + 1, q]\)

#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 5;int n, q, u[N], v[N], ans, sz[N], fa[N], len[N];char op[N];bool vis[N];map<pair<int, int>, int > dis;map<pair<int, int>, vector<int> > mp;vector<int> tr[N * 4];vector<pair<int, int> > stk;int find(int x) {if (fa[x] == x) {return x;}return find(fa[x]);
}bool merge(int x, int y) {x = find(x), y = find(y);if (x == y) {return 0;}if (sz[x] > sz[y]) {swap(x, y);}fa[x] = y;sz[y] += sz[x];stk.push_back({x, y});return true;
}void cancel() {auto [x, y] = stk.back();stk.pop_back();sz[y] -= sz[x];fa[x] = x;
}void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {int tot = 0;for (auto cur : tr[i]) {tot += merge(u[cur], v[cur]);}if (l == r) {if (vis[l]) {if (l == 4) {// cout << find(u[l]) << " " << find(v[l]) << "dfsafsafda\n";}cout << sz[find(u[l])] * sz[find(v[l])] << "\n";}}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}while (tot--) {cancel();}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> q;for (int i = 1; i <= n; i++) {fa[i] = i;sz[i] = 1;}for (int i = 1; i <= q; i++) {cin >> op[i] >> u[i] >> v[i];if (op[i] == 'A') {dis[{u[i], v[i]}] = i;}if (op[i] == 'Q') {mp[{u[i], v[i]}].push_back(i);vis[i] = true;}}for (int i = 1; i <= q; i++) {if (op[i] == 'Q') {continue;}if (!mp[{u[i], v[i]}].size()) {modify(1, 1, q, dis[{u[i], v[i]}], q, i);continue;}modify(1, 1, q, dis[{u[i], v[i]}], mp[{u[i], v[i]}][0] - 1, i);for (int j = 1; j < mp[{u[i], v[i]}].size(); j++) {if (mp[{u[i], v[i]}][j - 1] + 1 != mp[{u[i], v[i]}][j]) {modify(1, 1, q, mp[{u[i], v[i]}][j - 1] + 1, mp[{u[i], v[i]}][j] - 1, i);}}if (mp[{u[i], v[i]}][mp[{u[i], v[i]}].size() - 1] != q) {modify(1, 1, q, mp[{u[i], v[i]}][mp[{u[i], v[i]}].size() - 1] + 1, q, i);}}query(1, 1, q);return 0;
}

No Bug No Game

我们可以枚举最后一条边,也就是那个 \(sum + p_i > k\) 的 \(i\),那么 \(i\) 出现的区间就是 \([1, i - 1]\) 与 \([i + 1, q]\),合并时就等于每加入一个物品做一遍背包
code :

#include <bits/stdc++.h>using namespace std;const int N = 3e3 + 5;int n, k, a[N], w[N][15], p[N], tot, dp[N][N], ans;vector<int> tr[N * 4];void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {int now = tot;for (auto cur : tr[i]) {tot++;for (int j = 0; j <= k; j++) {dp[tot][j] = dp[tot - 1][j];if (j >= p[cur]) {dp[tot][j] = max(dp[tot][j], dp[tot - 1][j - p[cur]] + w[cur][p[cur]]);}}}if (l == r) {ans = max(ans, dp[tot][k]);for (int j = k - p[l] + 1; j < k; j++) {if (j >= 0) ans = max(ans, dp[tot][j] + w[l][k - j]);}}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}tot = now;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> k;for (int i = 1; i <= n; i++) {cin >> p[i];for (int j = 1; j <= p[i]; j++) {cin >> w[i][j];}}for (int i = 1; i <= n; i++) {if (i != 1) {modify(1, 1, n, 1, i - 1, i);}if (i != n) {modify(1, 1, n, i + 1, n, i);}}memset(dp, 0xcf, sizeof(dp));dp[0][0] = 0;for (int i = 1; i <= n; i++) {for (int j = 0; j <= k + 10; j++) {dp[i][j] = dp[i - 1][j];if (j >= p[i]) {dp[i][j] = max(dp[i][j], dp[i - 1][j - p[i]] + w[i][p[i]]);}if (j <= k) {ans = max(ans, dp[i][j]);}}}memset(dp, 0xcf, sizeof(dp));dp[0][0] = 0;query(1, 1, n);cout << ans;return 0;
}

Minimum Xor Pair Query

首先一个数出现的范围很明显,那么我们如何得出黑板上写的整数中两个整数的最小可能的按位异或值呢?我们可以维护一个 \(01\) 字典树,每插入一个数就找一遍最小的可能异或值即可
code :

#include <bits/stdc++.h>using namespace std;#define int long long const int N = 3e5 + 5;struct node {int son[2];
}trie[N * 31];int q, op[N], a[N], len[N], ans = 1e18, dcnt = 1, cnt[N * 31];bool vis[N];map<int, vector<int>> mp;vector<int> tr[N * 4];int query(int x) {int sum = 0, cur = 1;for (int i = 30; i >= 0; i--) {int a = (x >= (1 << i));x -= a * (1 << i);if (cnt[trie[cur].son[a]]) {cur = trie[cur].son[a];}else cur = trie[cur].son[a ^ 1], sum += (1 << i);}return sum;
}void insert(int x) {int cur = 1;for (int i = 30; i >= 0; i--) {int a = (x >= (1 << i));x -= a * (1 << i);if (!trie[cur].son[a]) trie[cur].son[a] = ++dcnt;cur = trie[cur].son[a];cnt[cur]++;}
}void erase(int x) {int cur = 1;for (int i = 30; i >= 0; i--) {int a = (x >= (1 << i));x -= a * (1 << i);if (!trie[cur].son[a]) trie[cur].son[a] = ++dcnt;cur = trie[cur].son[a];cnt[cur]--;}
}void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {int tot = 0, p = ans;for (auto cur : tr[i]) {ans = min(ans, query(a[cur]));insert(a[cur]);}if (l == r) {if (vis[l]) {cout << ans << "\n";}}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}for (auto cur : tr[i]) {erase(a[cur]);}ans = p;
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cin >> q;for (int i = 1; i <= q; i++) {cin >> op[i];if (op[i] == 1) {cin >> a[i];mp[a[i]].push_back(i);}else if (op[i] == 2) {cin >> a[i];len[mp[a[i]].back()] = (i - 1) - mp[a[i]].back() + 1;mp[a[i]].pop_back();}else {vis[i] = true;}}for (int i = 1; i <= q; i++) {if (op[i] != 1) {continue;}if (!len[i]) {len[i] = q - i;}modify(1, 1, q, i, i + len[i], i);}query(1, 1, q);return 0;
}

Make Q

对于一个点 \(cur\), 枚举他的三个临点 \(a, b, c\) 其中 \(a, b, c\) 互不相等,那么 \(cur\) 至 \(a\), \(cur\) 至 \(b\) 与 \(a\) 至 \(b\)可以形成一个环,那么\(cur\) 至 \(c\) 就是 "Q" 的那个角,如下图

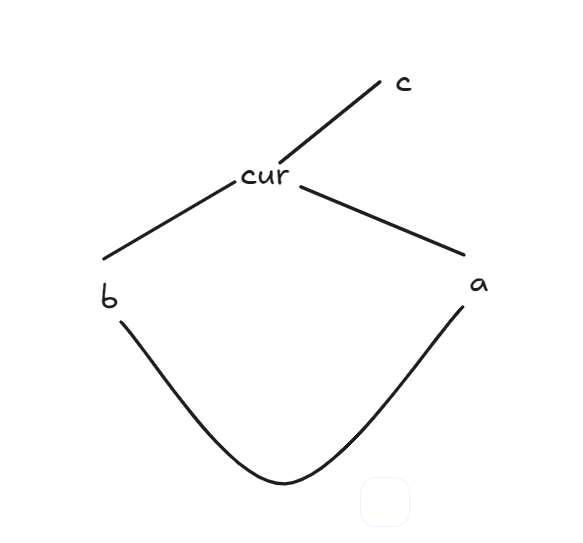
那不就是,一个点出现在 \([1, cur - 1]\) 与 \([cur + 1, n]\),在维护一下 \(floyd\) 即可
code :

#include <bits/stdc++.h>using namespace std;#define int long longconst int N = 3e2 + 5;struct node {int v, w;
};int n, m, tot, tmp[N * 5][N][N], dis[N][N], ans = 1e18;vector<int> tr[N * 5];vector<node> g[N];bool cmp(node _x, node _y) {return _x.w < _y.w;
}void modify(int i, int l, int r, int x, int y, int p) {if (l > y || r < x) {return ;}if (l >= x && r <= y) {tr[i].push_back(p);return ;}int mid = (l + r) >> 1;modify(i * 2, l, mid, x, y, p);modify(i * 2 + 1, mid + 1, r, x, y, p);
}void query(int i, int l, int r) {for (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {tmp[i][j][k] = dis[j][k];}}for (auto cur : tr[i]) {for (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {dis[j][k] = min(dis[j][k], dis[j][cur] + dis[cur][k]);}}}if (l == r) {for (node a : g[l]) {for (node b : g[l]) {if (a.v == b.v) {continue;}int cnt = 0;for (node c : g[l]) {if (cnt >= 5) {break;}if (c.v == a.v || c.v == b.v) {continue;}else {ans = min(ans, dis[a.v][b.v] + a.w + b.w + c.w);cnt++;}}}}}else {int mid = (l + r) >> 1;query(i * 2, l, mid);query(i * 2 + 1, mid + 1, r);}for (int j = 1; j <= n; j++) {for (int k = 1; k <= n; k++) {dis[j][k] = tmp[i][j][k];}}
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> m;memset(dis, 0x3f, sizeof(dis));for (int i = 1, u, v, w; i <= m; i++) {cin >> u >> v >> w;dis[u][v] = dis[v][u] = w;g[u].push_back({v, w});g[v].push_back({u, w});}for (int i = 1; i <= n; i++) {sort(g[i].begin(), g[i].end(), cmp);}for (int i = 1; i <= n; i++) {if (i != 1) {modify(1, 1, n, 1, i - 1, i);}if (i != n) {modify(1, 1, n, i + 1, n, i);}}query(1, 1, n);if (ans == 1e18) {cout << "-1";}else cout << ans;return 0;
}
/*
1 2
2 2 1
*/