AGC007F Shik and Copying String

涉及知识点：Ad-hoc，贪心

题意

Link

给出两个长度相同的字符串 \(S,T\)，定义一次操作为：

从头至尾处理每一位，每位可以变成上一位，或者不变。

求最少对 \(S\) 进行多少次操作使得 \(S=T\)。

思路

引理

可以发现，一次操作其实类似于选择一些点 \(l\)，从左到右覆盖它后面的点，并且如果记每个 \(l_i\) 覆盖的区间为 \([l_i,r_i]\)，满足这些区间无交集。

因此我们可以想到，将 \(T\) 中按相邻相同的字符划分成一些段，称这段为 \([l_i,r_i]\) 并且段内所有字符都为 \(T_{l_i}\)，显然让这些字符由离 \(l_i\) 最近的满足 \(S_j=T_{l_i},j\leq l_i\) 的 \(S_j\) 覆盖而来是最优的，下文我们把这样的 \(j\) 称为该段的 \(pre\)，另外下文有时用某个 \(pre\) 来指代覆盖某段的操作。

初始思路

于是我们想到了一个做法：先将 \(T\) 分段，然后倒序遍历 \(T\) 上每个段，对于每个段找到既小于该段段首也小于前一段 \(pre\) 的该段 \(pre\)。如果找到最后发现有些段找不到合法 \(pre\) 了则说明无解。至于如何计算最少操作次数，可以记录下每段 \([pre_i,r_i]\) 对应在 \(S\) 上存在的全局 \(pre\) 数量；此外如果 \(pre_i<l_i\)，那么说明它不能和左边的操作共存于一轮，还要 \(+1\)，取个 \(\max\) 作为答案。

这样是错误的。

改进思路

我们仔细思考刚才的思路有什么不妥之处：

1. 将 \(pre\) 视为静态。我们统计的时候将每段的 \(pre\) 都看成了静态的，但是实际上在一轮操作中，\(S_{pre_i}\) 可以通过操作而覆盖到 \(pre_{i+1}\) 的前面（当然同时得保证 \(pre_i\leq l_i\)），由于这么做不会覆盖到其他 \(pre\)，因此不会对影响合法性，但这样这个 \(pre_i\) 就会离 \(l_i\) 更近，这样一定是更优的。

   Example:

   考虑 \(S=\) abxxcdxxx，\(T=\) aaabbbbcd，根据我们之前的计算方法，答案应该为 4，即 d、c、b、a 依次覆盖。但我们发现实际上不用这么做，在第一轮操作时就可以同时操作 d 和 b 得到 abbbcdddd，然后再同时操作 a 和 c 得到 aaabccccd，最后操作 b 得到 aaabbbbcd，共 3 步。

2. 漏掉仍有冲突的 \(pre\)。我们只统计了与 \(pre_i\) 有冲突的 \(pre_j\)，并且想着如果让所有 \(pre_j\) 依次执行就不会有冲突，但是却没考虑 \(pre_j\) 在执行的过程中有可能会和更右边的 \(pre\) 发生冲突。

   Example:

   考虑 \(S=\) abcdef，\(T=\) aabcde，每个 \([pre_i,r_i]\) 区间内都只有至多 2 个 \(pre\)，但很明显不只是 2 个 \(pre\) 有冲突。

---

我们现在求每个段变为不影响它右边操作合法性，且不与它左边其他操作冲突的最小操作数，那么答案便为这些操作数的最大值。考虑用一个队列维护当前段 \([l_i,r_i]\) 会产生影响的 \(pre_j\) \((i\leq j)\)，从右到左逆序插入。

于是当我们逆序遍历到 \(i\) 时，处理分为两步：对 \(pre_i\) 右边的 \(pre\) 的处理，以及对 \(pre_i\) 本身的处理。

\(pre_i\) 右侧的处理

此时 \(pre_i\) 还未插入队列。

可以证明如果队头在 \(l_i\) 右侧且到 \(l_i\) 的距离大于队列中的元素个数，那么队头的操作合法性不受该段的影响，可以弹出。用代码表示即：while(!q.empty() && q.front()-(int)q.size()+1>l) q.pop();。

为什么？我们想象在段首设立一个“缓冲区”（我们队列维护的就是这个缓冲区），可以通过一系列操作把对该段以及该段右侧有影响的 \(pre\) 都搬到“缓冲区”里，并且保证他们的相对顺序不变。这样一来，这些之前在该段左侧的操作全部可以合法的转移到该段缓冲区中，这保证了这些操作不与左侧其他操作冲突；另外由于相对顺序不变，那么也不影响这些右侧操作的合法性。

而如果之前入队的某些 \(pre\) 在 \(l_i\) 右侧且到 \(l_i\) 的距离大于队列中的元素个数，那么这些 \(pre\) 即使不用缓冲区也可以保证上述两条性质，因此不用计入缓冲区。

为什么不用计入缓冲区？

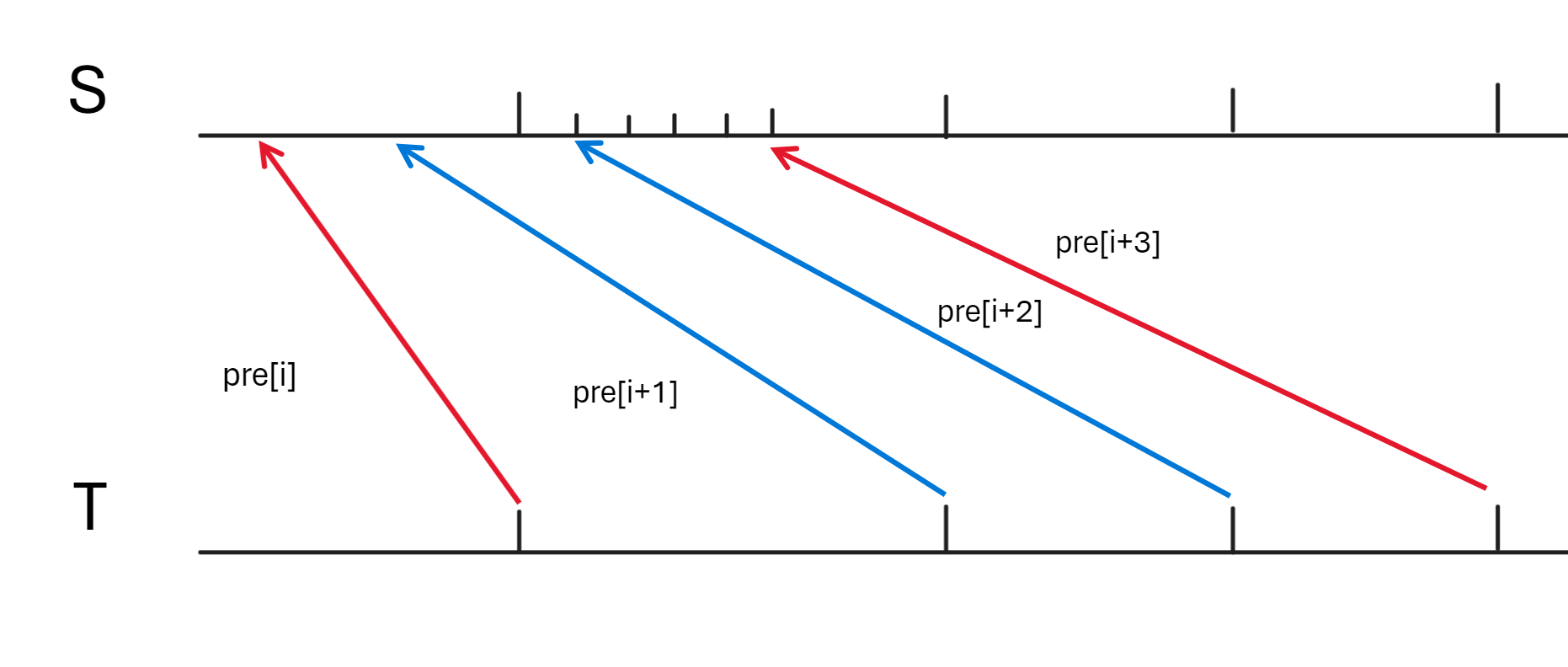
如下图，\(pre[i+3]\) 就是这样“不用记入”的 \(pre\)，因为不管它向后拓展与否，它都不影响左边其他的 \(pre[i+1],pre[i+2]\) 进入缓冲区，但 \(pre[i+2]\) 就是个反例，如果它不动，那么 \(pre[i+1]\) 就无法进入缓冲区，进而 \(pre[i]\) 就必须无法拓展到 \(l_i\) 上，对左侧造成了影响。

那这样的 \(pre\) 造成了贡献吗？

\(pre[i+3]\) 是有贡献的，但是它的操作可以与加入缓冲区的 \(pre\) 同时操作，因此没有独立的影响。事实上，\(pre[i+3]\) 的贡献是由遍历到段 \([l_{i+3},r_{i+3}]\) 的时候计算的，此时已经计算出了 \(pre[i+3]\) 不影响 \(pre[i]\) 时的操作数了。更多可以看完下文 “\(pre_i\) 本身的处理” 回来理解。

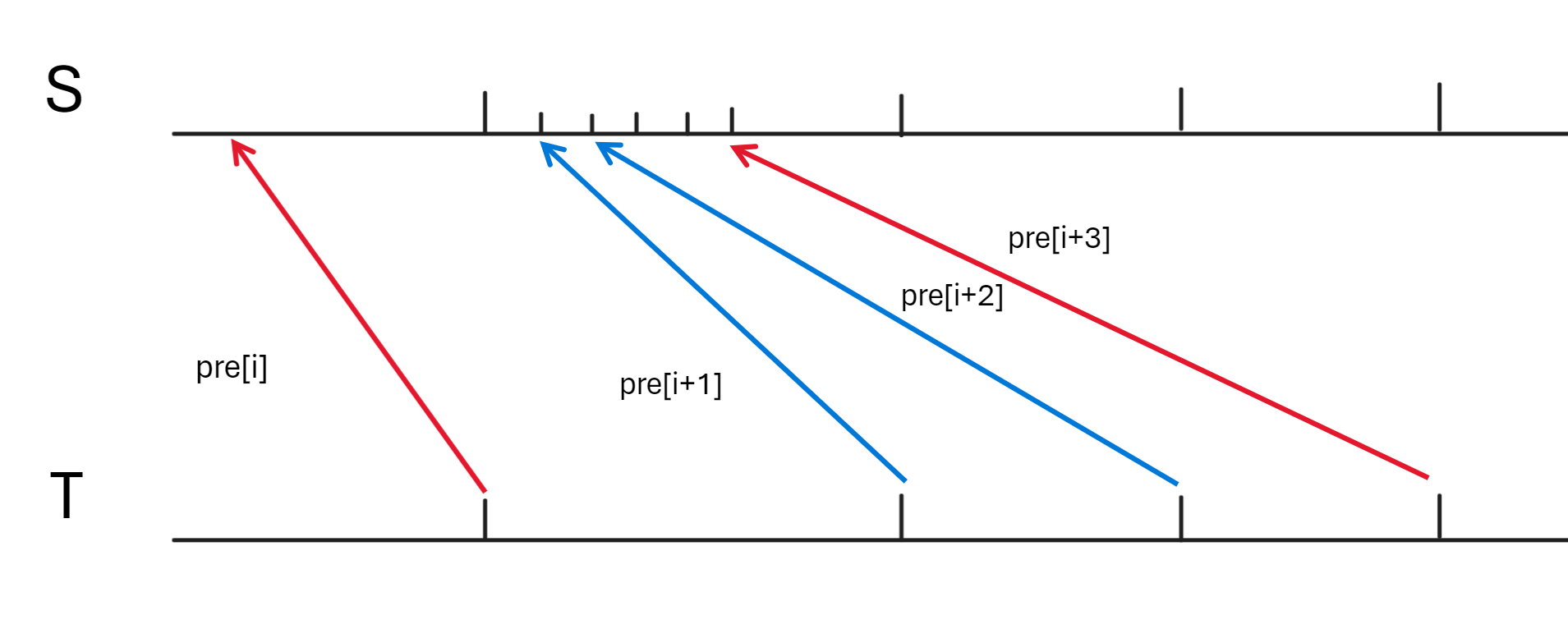
很明显，由于要保证相对顺序，上文中“一系列操作”的次数便为“缓冲区”的大小。

\(pre_i\) 本身的处理

此时 \(pre_i\) 已经插入队列。

根据定义，\(pre_i\) 不可能大于 \(l_i\)。

• \(pre_i < l_i\) 的情况：

  此时说明本段的 \(pre\) 会影响左侧的操作，因此为了满足 \(pre_i\) 不与左侧操作冲突，除了做完队列中的操作，还需要左侧额外覆盖一次多余的部分，如图，先覆盖蓝色再覆盖绿色：

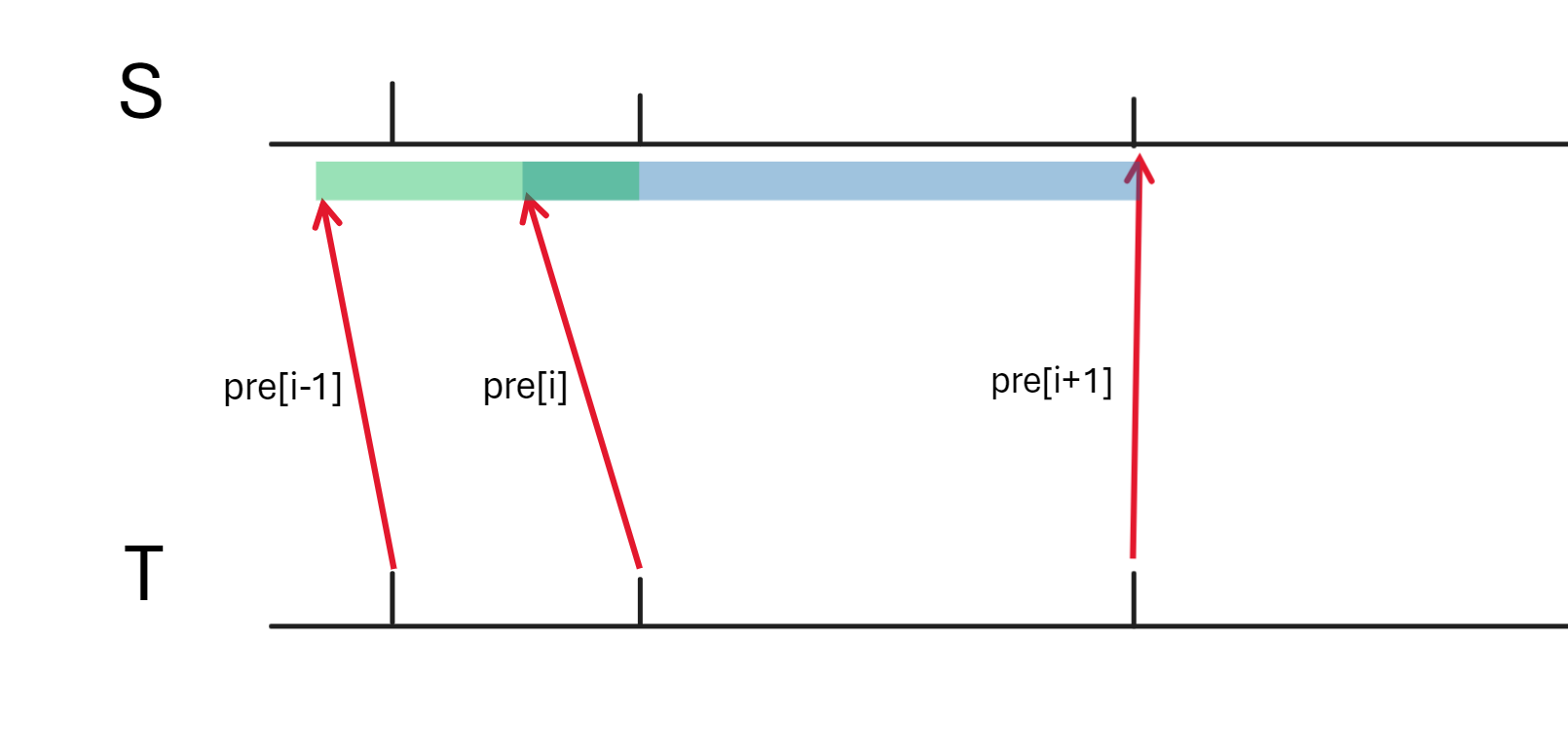
• \(pre_i=l_i\) 的情况：

  此时说明本段的 \(pre\) 不会影响左侧的操作，那么直接记录为“缓冲区”的大小即可。另外需特别注意如果 \(pre_{i+1}\) 不在本段内，即本段完全不影响右边的 \(pre\)，不能直接判断该段操作数为 \(1\)，还得判断该段 \(S\) 和 \(T\) 是否相同，如果相同则操作数只需要 \(0\)。

  实际上，对于 \(pre_i=l_i\) 且 \(pre_{i+1}\) 不在本段内的情况（代码 48~50 行）不需要额外处理，因为这个情况在处理 \(pre_{i+1}\) 的时候就由上一种情况处理过了。

代码

本体思路比较抽象，很难保证一遍理解，建议代码与分析结合食用。

#include<bits/stdc++.h>
#define mkp make_pair
using namespace std;
typedef pair<int,int> pii;
const int MAXN=3e6+5;
int n;
string s,t;
int fst[MAXN],ans=0;
int main(){freopen("string.in", "r", stdin);freopen("string.out", "w", stdout);ios::sync_with_stdio(false);cin>>n>>s>>t;if(s==t){cout<<0<<endl;return 0;}s=" "+s;t=" "+t;int rside=n;for(int i=n;i>=1;i--){if(t[i]!=t[i+1]){fst[rside]=i+1;rside=i;}}fst[rside]=1;queue<int>q;for(int l,r=n,pre=n,lstpre=n+1;r>=1;r=l-1){l=fst[r];if(pre>=l) pre=l;while(pre>=1 && s[pre]!=t[l]) pre--;if(pre<1){cout<<-1<<endl;return 0;}while(!q.empty() && q.front()-(int)q.size()+1>l) q.pop();q.push(pre);if(pre<l) ans=max(ans,(int)q.size()+1);else if(pre==l){bool flag=false;for(int i=l;i<=r;i++){if(s[i]!=t[i]){flag=true;break;}}if(flag) ans=max(ans,1);if(lstpre>r){//lstpre==r+1ans=max(ans,(int)flag);}else{ans=max(ans,(int)q.size());}}lstpre=pre;}cout<<ans<<endl;return 0;
}