调度问题





插入排序

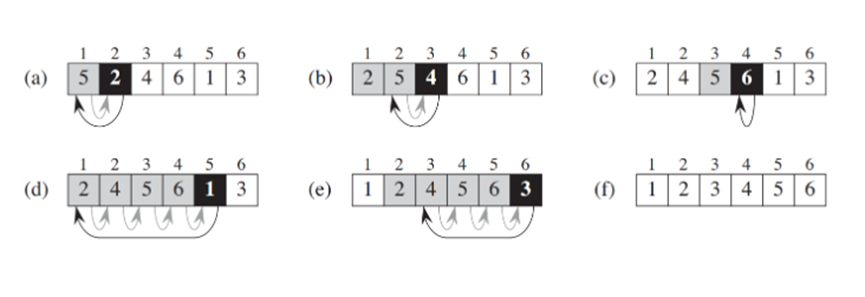

分治法
分治法是将原问题划分为多个规模较小的子问题,这些子问题可以独立求解,将子问题的解进行综合得到原问题的解。算法设计一般使用递归算法,算法分析一般使用递归表达式。


归并排序
归并排序,就是分组再合并,将一个数组等分为左右两个子数组,然后再使用归并排序递归地排序两个子数组,最后将两个子数组的排序结果进行合并。





快速排序算法
先确定一个数组的中间一个元素(枢轴),将数组划分为两个子数组,其中前面的数组元素都小于枢轴元素,后面的数组元素都大于枢轴元素。然后再递归地处理两个子数组。



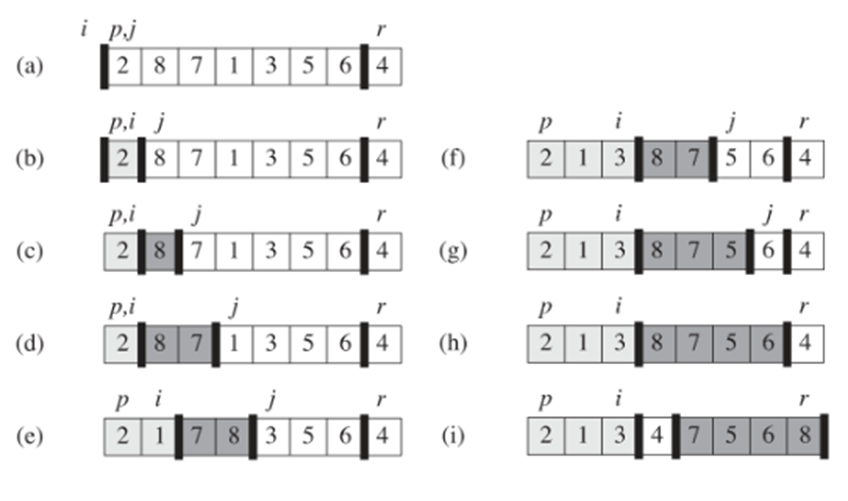
这里的快排算法,取最后一个元素作为枢轴,i和j之间的元素是大于枢轴的元素,i及其之前的元素是小于枢轴的元素,j及其之后的元素是未处理的元素。。
最坏情况是输入数组完全有序,时间复杂度为O(n2),因为确定一个枢轴需要遍历一遍数组,而又需要确立n个枢轴。最好和平均都是O(nlogn)。

选择问题



贪心算法
依据某种"短视的"贪心选择性质,问题求解表示成多步判断。期望通过局部优化选择达到全局优化选择,但贪心算法是否产生优化解,需要经过正确性证明。

活动选择问题
每次选择剩余时间最多的,通过局部最优解达到全局最优解。则按结束时间非降序排列,从前往后进行选择。
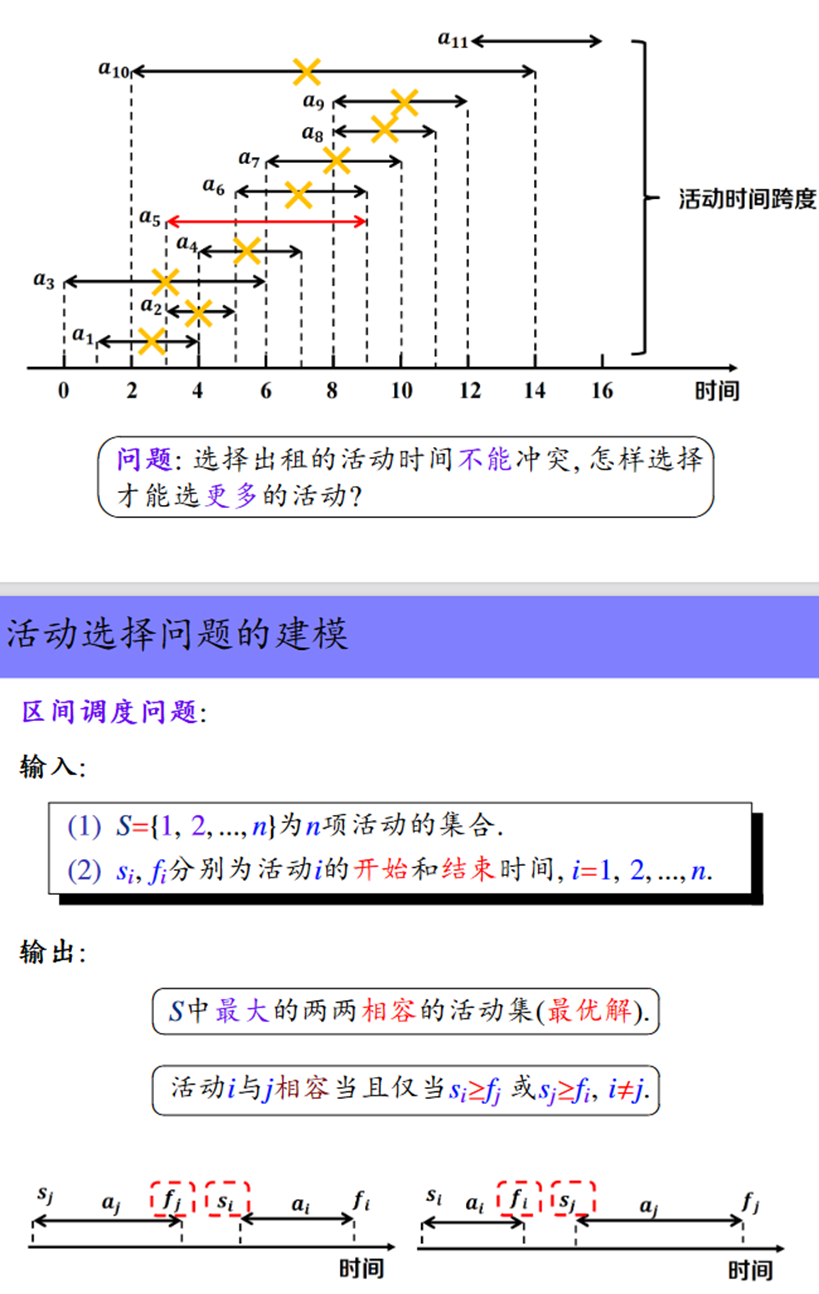

部分背包问题

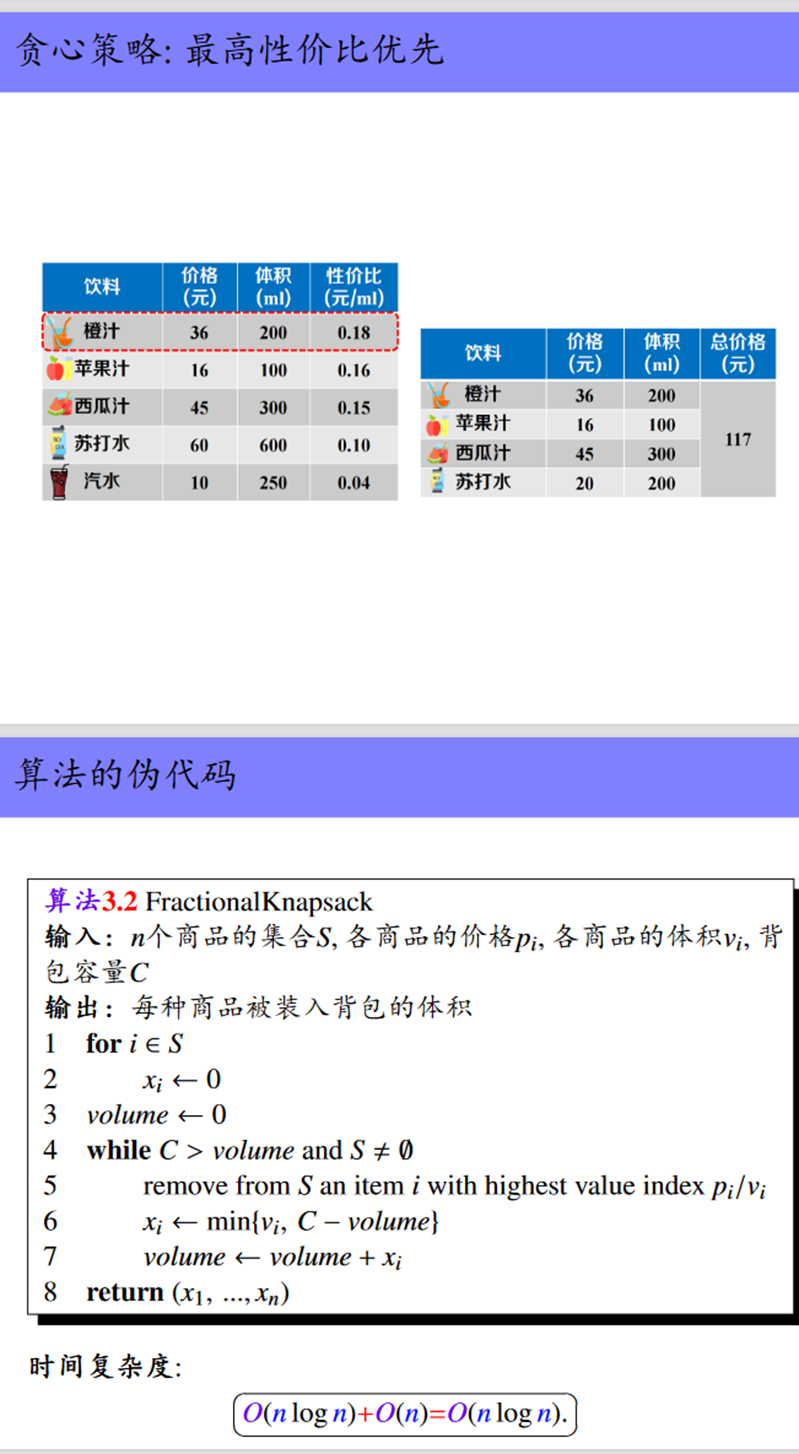
最小延迟调度问题

动态规划
动态规划法和分治法类似,也是将要求解的问题分解为一级一级、规模逐渐缩小的子问题,直到可以求解其解的子问题为止。所有子问题按层次关系构成一棵子问题树,树根是原问题,原问题的解依赖于子问题树中所有子问题的解。
与分治法不同的是,子问题往往不是独立的,子问题树中的子问题会有大量重复,对于重复的子问题,可以在第一次求解时将答案保存起来,后面遇到直接引用。
动态规划法求解的问题需要有优化子结构性质,即一个问题的优化解包含了子问题的优化解。



加权区间调度问题




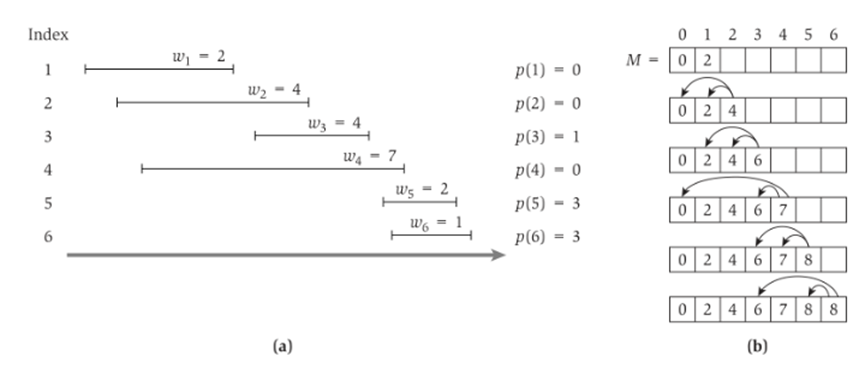

最长公共子序列问题
-
刻画结构特征
-
递归定义最优解的值
-
迭代计算最优解的值,并且记录构造最优解所需的信息
-
根据记录的信息构造最优解
这里计算最优解的值,是在一个矩阵中从上向下进行计算的,而构造最优解时,是反过来从下向上进行构造的。



标记函数b[I,j]的箭头是表示此处的值是从哪里来的,只有向左上角的箭头才是xi=yj的,并且等于左上角的值+1。


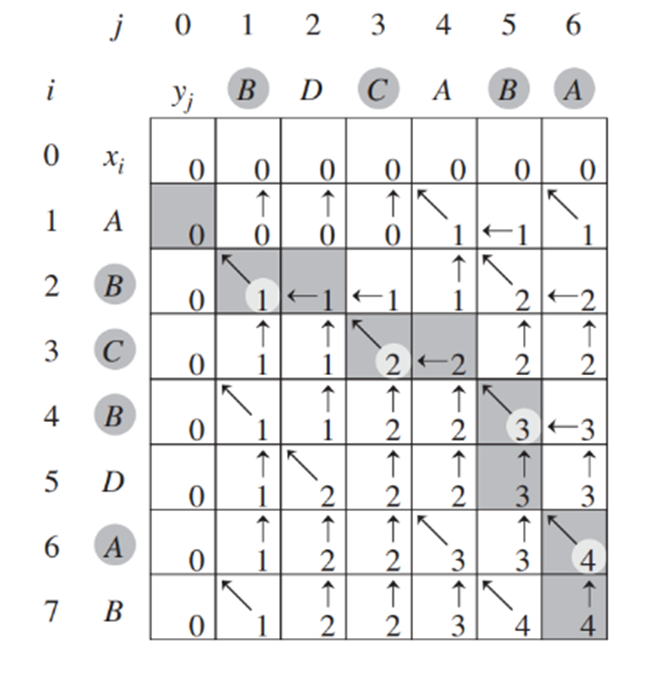
矩阵链乘法问题
首先两个矩阵Aij和矩阵Bjk相乘,最小乘法次数是i*j*k。





S用来标记划分点,便于后面构建最优解
向量P表示的是矩阵的行和列,如下
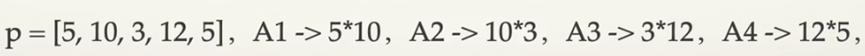
M矩阵如下,是一个上三角矩阵,对角线元素是0,计算时从左下到右上的每一层依次进行计算。

下面算法中r是矩阵链长度,从2到n,对应上图中左下到右上的每一层;i是行标,j是列标。

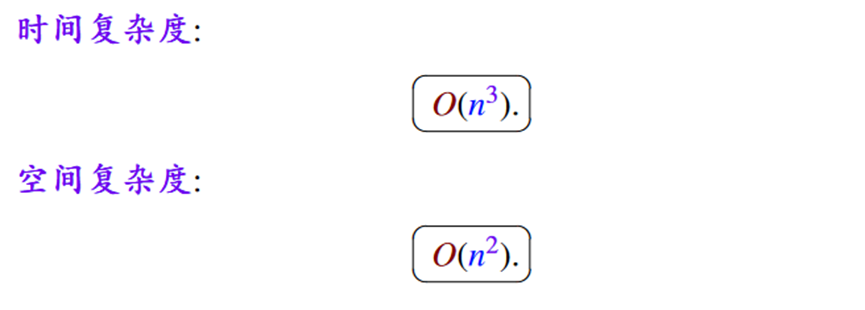

01背包问题

K(I,c)表示前i个商品中,背包容量为c时的最优解的值。
即是先考虑前1个商品,然后考虑前2个商品等,动态规划的思想就是利用优化子结构性质和重复子问题性质,这类问题的最优解包含着它们子问题的最优解,因此先从子问题的最优解算起。

特殊的01背包问题

子集合问题中,背包容量是W,价值和是元素和。
划分问题中,可以对整数集合求和,然后除以2得到平均值,拿平均值作为背包容量。所以问题就变成了判断能否从原集合中选择子集合,使子集合的整数和等于背包容量。
图
节点v从u可达:从节点u到节点v有一条路径
路径是简单的:路径上所有节点都是不同的
子图:V'包含于V,E'包含于E
生成子图:包含所有节点
树:连通无回路的无向图是树
森林:无回路的图是森林
生成树:图的一个生成子图,并且是一个树