Ciallo~(∠・ω< )⌒★ 我是赤川鹤鸣。本文假设您已经初步了解了 Hodgkin-Huxley Model,这里只是针对其中的公式的一些推导。不会对其优缺点、特性、应用等进行详述。
物理基础知识
如果已学习过物理学中电流、电容、电导率的概念,可跳过此节。
首先,让我们复习一下物理学中电流、电容、电导率的概念。
电流强度是单位时间内通过导体某一横截面的电荷量,简称电流,符号为 \(I\)。
\[I = \dfrac{\text{d}q}{\text{d}t} \tag{1.1}
\]
其中 \(q\) 是电荷量,\(t\) 是时间。
电容量在数值上等于一个导电极板上的电荷量与两个极板之间的电压之比,简称电容,符号为 \(C\)。
\[C = \dfrac{q}{V} \tag{1.2}
\]
其中 \(q\) 是一个导电极板上的电荷量,\(V\) 是两个极板之间的电压。
把式 \((1.2)\) 代入到式 \((1.1)\) 中,则
\[I = \dfrac{\text{d}(CV)}{\text{d}t} = C\dfrac{\text{d}V}{\text{d}t} \tag{1.3}
\]
电导率是用来描述物质中电荷流动难易程度的参数,符号为 \(g\)。
\[g = \dfrac{I}{U} \tag{1.4}
\]
数学基础知识
如果已学习过微分方程的解法,可跳过此节。
接下来,我们分别推导一阶齐次线性微分方程和一阶非齐次线性微分方程的通解。
一阶齐次线性微分方程的通解推导
例如,有如下的一阶齐次线性微分方程
\[\dfrac{\text{d}y}{\text{d}x} + P(x)y = 0 \ \ (y \neq 0)
\]
两侧除以 \(y\) 并乘 \(\text{d}x\),得
\[\dfrac{\text{d}y}{y} + P(x)\text{d}x = 0
\]
移项,得
\[\dfrac{\text{d}y}{y} = - P(x)\text{d}x
\]
两侧积分,得
\[\int{\dfrac{\text{d}y}{y}} = \int{ - P(x)\text{d}x}
\]
因为 \(\ln{y} + \ln{C}\) 的导数是 \(\dfrac{1}{y}\),所以
\[\ln y = \int{ - P(x)\text{d}x} + \ln C
\]
换成以自然对数 \(e\) 为底的形式,即
\[e^{\ln{y}} = e^{\int{ - P(x)\text{d}x} + \ln C} = e^{- \int{P(x)\text{d}x}} e^{\ln C}
\]
由于 C 只是一个常数,为了方便,最终通解可写为
\[y = C e^{- \int{P(x)\text{d}x}} \tag{2.1}
\]
一阶非齐次线性微分方程的通解推导
例如,有如下的一阶非齐次线性微分方程
\[\frac{\text{d}y}{\text{d}x} + P(x)y = Q(x) \tag{2.2}
\]
根据式 \((2.1)\),令 \(C = u(x)\),得
\[y = u(x) e^{- \int{P(x)\text{d}x}} \tag{2.3}
\]
带入原方程 \((2.2)\) 得
\[\frac{\text{d}u}{\text{d}x} = \dfrac{Q(x)}{e^{- \int{P(x)\text{d}x}}}
\]
对 \(\frac{\text{d}u}{\text{d}x}\) 积分得 \(u(x)\) 并带入式 \((2.3)\) 得
\[y = C e^{- \int{P(x)\text{d}x}} + e^{- \int{P(x)\text{d}x}} \int Q(x) e^{ \int{P(x)\text{d}x}} \text{d}x
\]
Hodgkin-Huxley Model
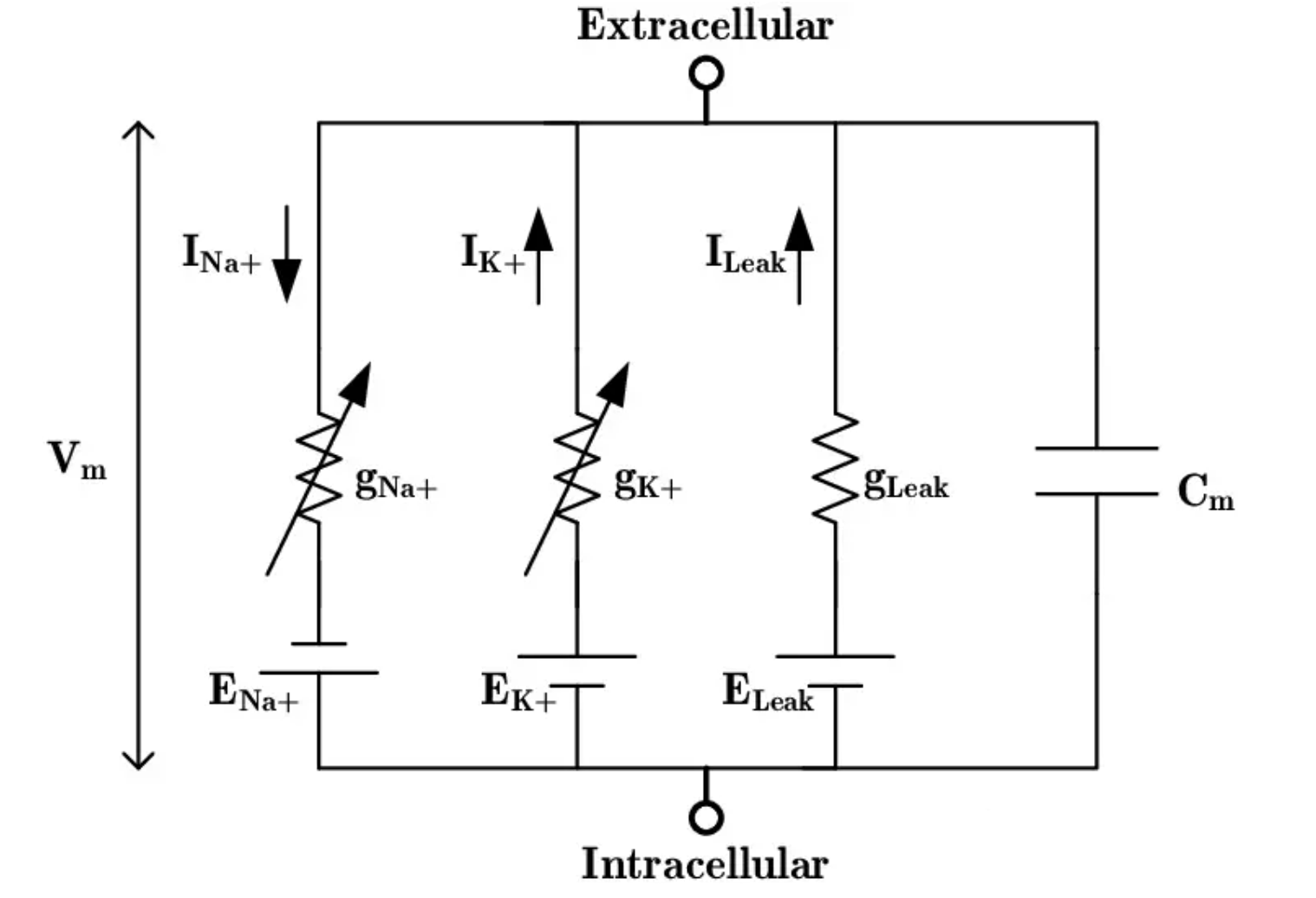
Hodgkin-Huxley Model 的结构如图所示,可以看出膜电流 \(I_{\text{m}}\) 是由钠离子电流\(I_{\text{Na+}}\)、钾离子电流 \(I_{\text{K+}}\)、漏电电流 \(I_{\text{Leak}}\) 和电容器电流 \(I_{C}\) 组成的,即
\[I_{\text{m}} = I_{\text{Na+}} + I_{\text{K+}} + I_{\text{Leak}} + I_{C} \tag{3.1}
\]
接下来我们依次推导各个通道上的电流计算公式。
通道电流计算公式
钠离子通道电流
根据式 \((1.4)\),钠离子通道上的电流 \(I_{\text{Na+}}\) 就可由下式决定
\[I_{\text{Na+}} \left( V_{\text{m}}, t \right) = g_{\text{Na+}}\left( V_{\text{m}}, t \right) (V_{\text{m}} - E_{\text{Na+}})
\]
其中钠离子通道上的电导率 \(g_{\text{Na+}}\left( V_{\text{m}}, t \right)\) 是一个与膜电压 \(V_{\text{m}}\) 和时间 \(t\) 相关的函数。为了更好地研究这个函数,我们使用钠离子通道在膜电压 \(V_{\text{m}}\) 和时间 \(t\) 下打开的概率函数 \(P_{\text{Na+}} \left(V_{\text{m}}, t \right)\)、钠离子通道的个数 \(N_{\text{Na+}}\) 和单个钠离子通道的电导率 \(\hat{g}_{\text{Na+}}\) 进行表示,即
\[g_{\text{Na+}}\left( V_{\text{m}}, t \right) = P_{\text{Na+}} \left(V_{\text{m}}, t \right) N_{\text{Na+}} \hat{g}_{\text{Na+}} \tag{3.2}
\]
通常,还使用门限变量来重写公式 \((3.2)\) 为
\[g_{\text{Na+}}\left( V_{\text{m}}, t \right) = \bar{g}_{\text{Na+}} m^3 \left( V_{\text{m}}, t \right) h \left( V_{\text{m}}, t \right) \tag{3.3}
\]
其中 \(\bar{g}_{\text{Na+}}\) 是钠离子通道的平均电导率,\(m\) 和 \(h\) 是两个与膜电压 \(V_{\text{m}}\) 和时间 \(t\) 相关的门限变量,因为钠离子通道含有两种状态——激活与非激活。
钾离子通道电流
同理,也可以得到钾离子通道上的电流计算公式
\[I_{\text{K+}} \left( V_{\text{m}}, t \right) = g_{\text{K+}}\left( V_{\text{m}}, t \right) (V_{\text{m}} - E_{\text{K+}})
\]
\[g_{\text{K+}}\left( V_{\text{m}}, t \right) =
P_{\text{K+}} \left(V_{\text{m}}, t \right) N_{\text{K+}} \hat{g}_{\text{K+}}
= \bar{g}_{\text{K+}} n^4 \left( V_{\text{m}}, t \right) \tag{3.4}
\]
漏电通道电流
可以得到漏电通道电流的公式
\[I_{\text{Leak}} = g_{\text{Leak}} (V_{\text{m}} - E_{\text{Leak}})
\]
其中 \(g_{\text{Leak}}\) 是漏电通道上的电导率,\(V_{\text{m}}\) 是膜电压,\(E_{\text{Leak}}\) 是漏电通道上的电势差。
电容通道电流
根据公式 \((1.3)\),可以得到电容通道电流的公式
\[I_{\text{C}} = C_{\text{m}}\dfrac{\text{d}V_{\text{m}}}{\text{d}t}
\]
其中 \(C_m\) 是膜电容,\(V_{\text{m}}\) 是膜电压,\(t\) 是时间。
电导率计算公式
从式 \((3.3)\) 和 \((3.4)\) 中,我们知道了 \(m\)、\(n\)、\(h\) 三种门限变量,但是其具体的内部构造仍不清楚。我们不妨将门限变量统一设为 \(\varphi(t)\),并由 \(\alpha_{\varphi}\) 和 \(\beta_{\varphi}\) 两个因子决定,即
\[\frac{\text{d}\varphi}{\text{d}t} = \alpha_{\varphi} (1 - \varphi) - \beta_{\varphi} \varphi \tag{3.5}
\]
整理式 \((3.5)\) ,按照一阶非齐次线性微分方程的一般形式,可得
\[\frac{\text{d}\varphi}{\text{d}t} + (\alpha_{\varphi} + \beta_{\varphi}) \varphi = \alpha_{\varphi}
\]
这样根据一阶非齐次线性微分方程的通解,可求得
\[\begin{align*}\varphi(t) &= Ce^{-(\alpha_{\varphi} + \beta_{\varphi})t} + e^{-(\alpha_{\varphi} + \beta_{\varphi})t} \int \alpha_{\varphi} e^{(\alpha_{\varphi} + \beta_{\varphi})t} \text{d} t \\&= Ce^{-(\alpha_{\varphi} + \beta_{\varphi})t} + e^{-(\alpha_{\varphi} + \beta)t} \cdot \dfrac{\alpha_{\varphi}}{\alpha_{\varphi} + \beta_{\varphi}} \cdot e^{(\alpha_{\varphi} + \beta_{\varphi}) t} \\&= C e^{-(\alpha_{\varphi} + \beta_{\varphi})t} + \dfrac{\alpha_{\varphi}}{\alpha_{\varphi} + \beta_{\varphi}}
\end{align*}
\]
还可以看出一些性质
\[\varphi(0) = C + \dfrac{\alpha_{\varphi}}{\alpha_{\varphi} + \beta_{\varphi}}
\]
\[\varphi(+ \infty) = \dfrac{\alpha_{\varphi}}{\alpha_{\varphi} + \beta_{\varphi}}
\]
令 \(\tau_{\varphi} = \dfrac{1}{\alpha_{\varphi} + \beta_{\varphi}}\),
\[\varphi(t) = \left( \varphi(0) - \varphi(+ \infty) \right) e^{-\frac{t}{\tau_{\varphi}}} + \varphi(+\infty)
\]
也等价于
\[\varphi(t) = \varphi(0) - \left( \varphi(0) - \varphi(+ \infty) \right) \left( 1 -e^{-\frac{t}{\tau_{\varphi}}} \right)
\]
综上,根据 \(m\)、\(n\)、\(h\) 三种门限变量和式,我们都可以从微分方程得到原函数的表达式,这里给出各个门限变量的微分方程
\[\dfrac{\text{d}n}{\text{d}t} = \alpha_n (V_{\text{m}}) \left(1 - n(t)\right) - \beta_{n}(V_{\text{m}})n(t)
\]
\[\dfrac{\text{d}m}{\text{d}t} = \alpha_m (V_{\text{m}}) \left(1 - m(t)\right) - \beta_{m}(V_{\text{m}})m(t)
\]
\[\dfrac{\text{d}h}{\text{d}t} = \alpha_h (V_{\text{m}}) \left(1 - h(t)\right) - \beta_{h}(V_{\text{m}})h(t)
\]
具体到 \(\alpha_{\varphi}\) 和 \(\beta_{\varphi}\) 的计算,它们是由实验数据拟合的,因此不同的细胞类型也具有不同的 \(\alpha_{\varphi}\) 和 \(\beta_{\varphi}\) 。
总结
Hodgkin-Huxley Model 中细胞膜电流的计算公式为
\[\begin{align*}I_{\text{m}} \left( V_{\text{m}}, t \right) &= \bar{g}_{\text{Na+}} \cdot m^3 \left( V_{\text{m}}, t \right) \cdot h \left( V_{\text{m}}, t \right) \cdot \left( V_{\text{m}} - E_{\text{Na+}} \right) \\&+ \bar{g}_{\text{K+}} \cdot n^4 \left( V_{\text{m}}, t \right) \cdot \left( V_{\text{m}} - E_{\text{K+}} \right) \\&+ g_{\text{Leak}} \left( V_{\text{m}} - E_{\text{K+}} \right) \\&+ C_{\text{m}} \dfrac{\text{d} V_{\text{m}}}{\text{d} t}
\end{align*}
\]