第十一章图论 Part8

news/2024/11/15 0:39:30/文章来源:https://www.cnblogs.com/haohaoscnblogs/p/18409954

单源最短路径算法
- dijkstra（朴素版）
  - 适用范围（权值不能为负数的单源最短路径）
  - 思路
  - 算法正确性
拓扑排序
- 思路
心得

单源最短路径算法

dijkstra（朴素版）

适用范围（权值不能为负数的单源最短路径）

思路

基本类似Prim算法，只是新加入（确定）点的时候，当前算法算的是距离源点的最短路径，而Prim算法算的是距离最小生成树的最短路径。

minValVec 记录当前每个点到源点的最短路径（随着遍历的过程而更新）
每次并入的步骤：

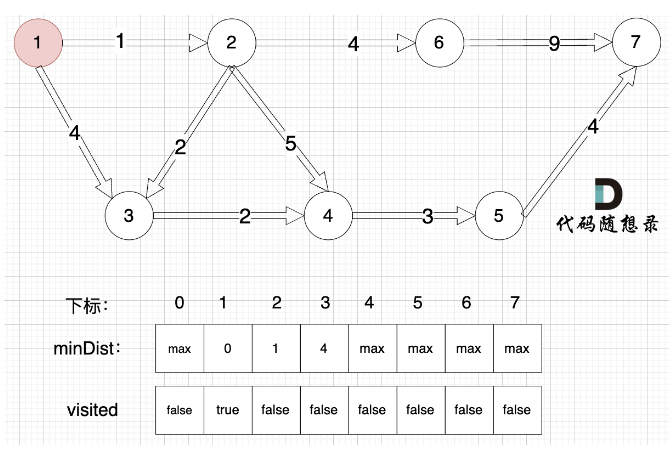
确定选哪个节点并入（不在已访问节点中，距离源点最小的节点）遍历每个点，得到最小距离的那个点及最小距离。 (顶点编号）
将第一步选到的点加入到visited中，用一个bool列表记录已经访问的点。
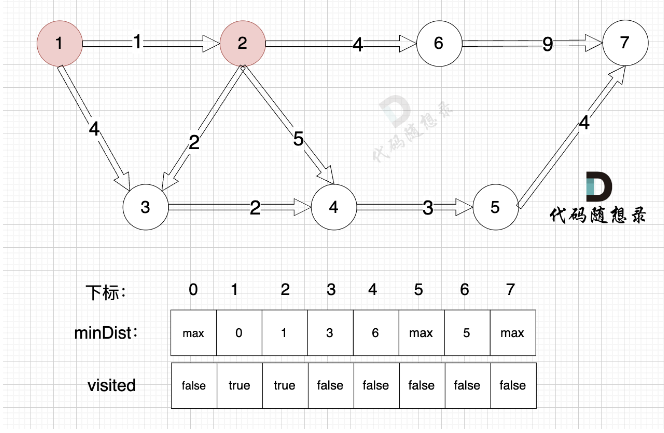
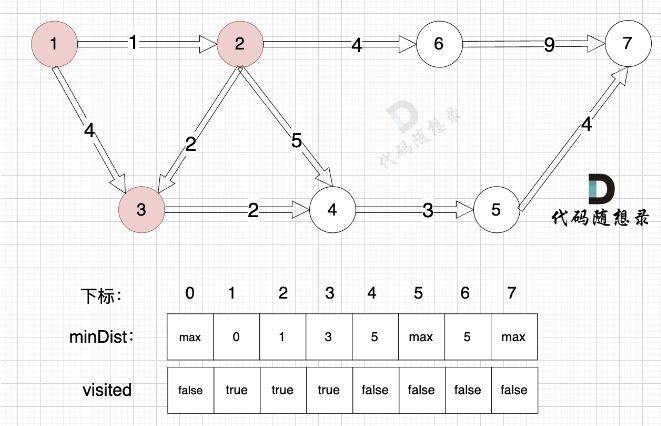
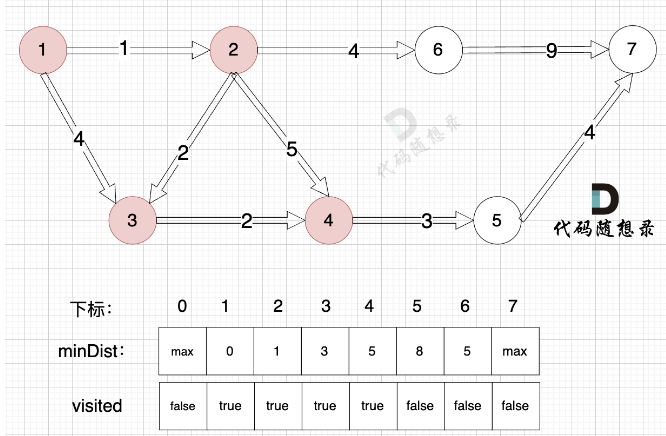
更新未访问的节点到源点的距离。（与cur相连的j节点距离源点的距离，比cur加入之前j节点到源点的距离小） =》因为cur变成访问过的节点后，其他节点需要更新距离这个最新形成的与源点的距离） =》观察4这个节点随着各个节点的加入，距离源点的最短路径的变化；以及最终作为被选取的点和确认该点最短路径的过程。

如果想记录这个最短路径的边，则使用parent数组（元素值表示使当前节点更新的前一个节点），在第三步更新时记录即可，如果后续节点的加入还会使该点更新，则parent数组实际也会更新。

v,e = map(int,input().split()) # 顶点数，边数
graph = [[float('inf')]* (v+1) for _ in range(v+1)] #邻接矩阵for _ in range(e):x,y,k = map(int,input().split())#有向图graph[x][y] = kvisited = [False]* (v+1) #是否访问过
minValVec = [float('inf')]* (v+1) #所有点的最小距离列表,初始化每个距离为inf
minValVec[1] = 0 #源点到自己的距离为0for i in range(1,v+1):  # 确认每个点的最短距离#1. 确认新加入的点的编号(谁距离源点最近就加谁）cur = -1minDist = float('inf') #最大的权值 for j in range(1,v+1): #遍历所有还未访问点，确认要新加入的点的编号if not visited[j] and minValVec[j] < minDist:minDist = minValVec[j] #更新最小距离,以便在后续迭代中继续比较cur = j #更新新加入的点的编号，当循环退出时，确定新加入的点的编号if cur == -1: #未找到最小距离的点，说明剩下的点和已经访问的点不连通，退出循环break#2.记录新加入的点visited[cur] = True#3.因为路径中有了新加入的点，更新每个未确定的点到源点的最小距离for j in range(1,v+1):if (not visited[j] and graph[cur][j] != float('inf') and minValVec[cur] +  graph[cur][j] < minValVec[j]):#某点到源点的距离可能由于新加入了点而改变minValVec[j] = minValVec[cur] +  graph[cur][j]minValVec[v] = -1 if minValVec[v] == float('inf') else minValVec[v]
print(minValVec[v])

算法正确性

那么这个算法为什么就能确定是最短路径呢？实际上按照算法的步骤解释，我们每次选择距离某点的相邻节点时，都是选择最短的（距离源点），假设值为x，而其他的路径非最短，假设值为y1,y2...，那么绕路的话,假设绕路的边的长度为z1,z2...，由于x < y1,y2... 所以x < y1+ z1,y2+z2.（由于算法的适用范围，权值必须非负，所以这里的x,y,z均大于等于0）.. ,就更不可能作为最短路径的选取。简单的说，就是每次选距离源点最短的保证了没有其他方式可以使得这个距离更短。
这也是权值必须非负的原因。反例如下：

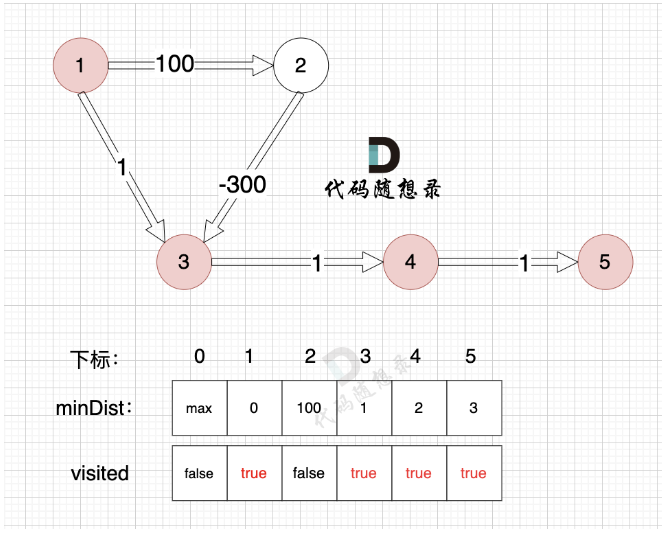
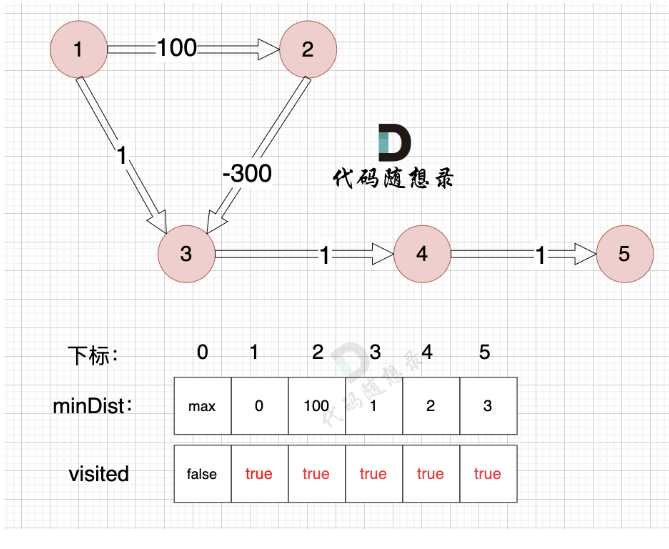
相当于先走一个长路，然后绕路比直接走反而可以使到源点最短路径更短，所以该算法要求权值非负。

拓扑排序

拓扑排序是经典的图论问题。

先说说拓扑排序的应用场景。

大学排课，例如先上A课，才能上B课，上了B课才能上C课，上了A课才能上D课，等等一系列这样的依赖顺序。问给规划出一条完整的上课顺序。

拓扑排序在文件处理上也有应用，我们在做项目安装文件包的时候，经常发现复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。

思路

找到当前入度为0的点（当前入度为0的节点是由zerolist来记录的），加入到结果集，删除它对原图的影响(更新它影响节点的入度，即它的出边连接的点的入度减1），继续这一过程，直到zerolist中没有节点，此时结束，res中记录的即是拓扑排序的过程，表示找完或者没有入度为0的点（有环）。

v,e = map(int,input().split()) # 顶点数，边数
graph = [[float('inf')]* (v+1) for _ in range(v+1)] #邻接矩阵inDegree = [0] * v #剩余入度（随着选取的进行会更新）
for _ in range(e):x,y = map(int,input().split())#有向图graph[x][y] = 1inDegree[y] += 1from collections import deque
#剩余入度为0的点(用deque是为了删除头部时复杂度o(1)
zeroList = deque()
for i in range(len(inDegree)):if inDegree[i] == 0:zeroList.append(i)#拓扑排序的结果放入res
res = []
while(len(zeroList) > 0):cur = zeroList.popleft()res.append(cur)#更新该点影响的点的入度,若修改后入度为0，则加入到zero列表中for i in range(v):if graph[cur][i] == 1:inDegree[i] -= 1if inDegree[i] == 0:zeroList.append(i)
#print(res) 
if len(res) != v:print('-1')
else:print(' '.join(map(str,res)))