1 2022 CSP-J 阅读程序3
阅读程序(程序输入不超过数组或字符串定义的范围;判断题正确填 √,错误填×;除特 殊说明外,判断题 1.5 分,选择题 3 分)
源代码
#include<iostream>using namespace std;int n,k;int solve1()
{int l=0,r=n;while(l<=r){int mid=(l+r)/2;if(mid * mid <=n) l=mid+1;else r=mid-1;}return l-1;
}double solve2(double x)
{if(x == 0) return x;for(int i=0;i<k;i++)x=(x+n/x)/2;return x;
}int main()
{cin>>n>>k;double ans=solve2(solve1());cout<<ans<<' '<<(ans * ans == n)<<endl;return 0;
}假设int为32位有符号整数类型,输入的n是不超过47000的自然数、k是不超过int表示范围的自然数,完成下面的判断题和单选题
判断题
28.该算法最准确的时间复杂度分析结果为O(logn+k) ( )
29.当输入为"9801 1"时,输出的第一个数为"99" 。( )
30.对于任意输入的n,随着所输入k的增大,输出的第2个数会变成"1" 。( )
31.该程序有存在缺陷。当输入的n过大时,第12行的乘法有可能溢出,因此应当将mid强制转换为64位整数再计算。( )
单选题
32.当输入为 “2 1” 时,输出的第一个数最接近( )
A. 1
B. 1.414
C. 1.5
D. 2
33.当输入"3 10"时,输出的第一个数最接近( )
A. 1.7
B. 1.732
C. 1.75
D. 2
34.当输入为"256 11"时,输出的第一个数( )
A. 等于16
B. 接近但小于16
C. 接近但大于16
D. 前三种情况都有可能
2 相关知识点
1) 算法时间复杂度
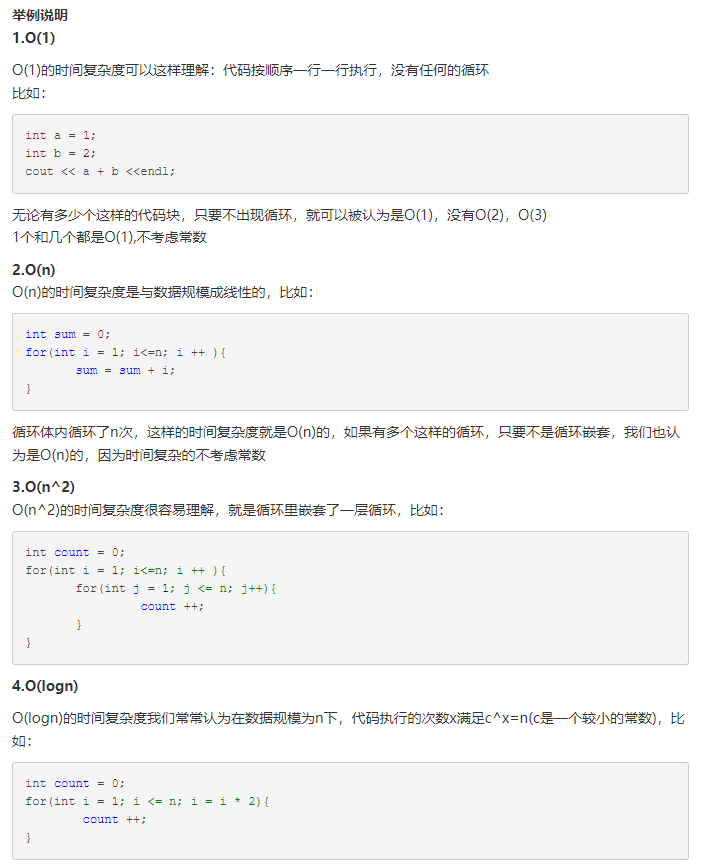
算法时间复杂度定性描述该算法的运行时间,常用大O符号表述
常用时间复杂度举例
2) 二分答案
二分答案顾名思义,它用二分的方法枚举答案,并且枚举时判断这个答案是否可行
直接对答案进行枚举查找,接着判断答案是否合法。如果合法,就将答案二分进一步靠近,如果不合法,就接着二分缩小判断。这样就可以大大的减少时间。
二分中有时可以得可行得答案,但不是最大的,继续向右靠近,求出最大值
示例
int ans = 1;int l = 1,r = 100000;//在1~100000之间的整数枚举 while(l <= r){int m = l + (r - l) / 2;if(check(m)){//满足 则进行向右缩小范围 看看有没有更大的 ans = m;//可能多次赋值 最后一定是可能的最大值 l = m + 1;}else{//不满足缩小边长 向左缩小范围 用更小边长继续尝试 r = m - 1;} }二分查找时间复杂度分析
二分查找每次都缩小或扩大为原来的一半和上面示例4类似,所以也是Olog(n)
3 思路分析
solve1函数
int solve1()
{int l=0,r=n;while(l<=r){int mid=(l+r)/2;if(mid * mid <=n) l=mid+1;else r=mid-1;}return l-1;
}solve1函数是一个标准的二分答案算法,找到1个数x ,使得x * x 无限接近于n
也就是求n的平方根,当n=4时进行验证
n=4 l=0 r=4
//0<=4 进入循环
//第1次循环
mid=(l+r)/2=(0+4)/2=2 ,mid * mid =2 * 2=4<=4 条件满足 l=mid+1=2+1=3 r=4
//3<=4 条件满足
//第2次循环
mid=(l+r)/2=(3+4)/2=3, mid * mid =3 * 3 =9<=4 不满足,r=mid-1=3-1=2 l=3
//3<=2 条件不满足 退出循环
//返回 l-1 = 3 -1 =2
//所以当n=4时,函数solve1返回2,是4得平方根如果n=5,是否也可以算出其平方根呢?
n=5 l=0 r=5
//0<=5 进入循环
//第1次循环
mid=(l+r)/2=(0+5)/2=2 ,mid * mid =2 * 2=4<=5 条件满足 l=mid+1=2+1=3 r=5
//3<=5 条件满足
//第2次循环
mid=(l+r)/2=(3+5)/2=4, mid * mid =4 * 4 =16<=5 不满足,r=mid-1=4-1=3 l=3
//3<=3 条件满足
//第3次循环
mid=(l+r)/2=(3+3)/2=3, mid * mid =3 * 3 =9<=5 不满足,r=mid-1=3-1=2 l=3
//3<=2 条件不满足 退出循环
//返回 l-1 = 3 -1 =2
//所以当n=5时,函数solve1返回2,不是5得平方根,2是小于5平方根得最大整数根据如下代码,可以大概猜测solve2是辅助求出平方根是小数的情况,如果猜不出,可以模拟对应数据
double ans=solve2(solve1());
cout<<ans<<' '<<(ans * ans == n)<<endl;假设int为32位有符号整数类型,输入的n是不超过47000的自然数、k是不超过int表示范围的自然数,完成下面的判断题和单选题
判断题
28.该算法最准确的时间复杂度分析结果为O(logn+k) ( T )
分析
此题调用了2次函数,solve1和solve2,其中solve1是二分答案,时间复杂度为O(logn),solve2的时间复杂度为O(k)
所以准确的时间复杂度为2者之和O(logn+k)
29.当输入为"9801 1"时,输出的第一个数为"99" 。( T )
分析
n=9801 ,求其对应平方根是99
k为1,执行1次 x = (x + n / x) / 2;
x=(99 + 9801/99)/2=99
所以是99
30.对于任意输入的n,随着所输入k的增大,输出的第2个数会变成"1" 。( F )
分析
如果平方根不是整数,求出结果没有精确的值,只能计算n的近似值,所以不会相等,返回false为0
31.该程序有存在缺陷。当输入的n过大时,第12行的乘法有可能溢出,因此应当将mid强制转换为64位整数再计算。( F )
分析
n最大是47000,中间可能导致溢出的是mid * mid,最大是(47000/2)*(47000/2)不会超过int的表示范围21亿
单选题
32.当输入为 “2 1” 时,输出的第一个数最接近( C )
A. 1
B. 1.414
C. 1.5
D. 2
分析
当n=2时,solve1求出平方根整数为1
//模拟过程
n=2 l=0 r=2
//0<=2 进入循环
//第1次循环
mid=(l+r)/2=(0+2)/2=1 ,mid * mid =1 * 1=1<=2 条件满足 l=mid+1=1+1=2 r=2
//2<=2 条件满足
//第2次循环
mid=(l+r)/2=(2+2)/2=2, mid * mid =2 * 2 =4<=2 不满足,r=mid-1=2-1=1 l=2
//2<=1 条件不满足 退出循环
//返回 l-1 = 2 -1 =1k为1,执行1次 x = (x + n / x) / 2;
x=(1+2/1)/2=1.5
所以选C
33.当输入"3 10"时,输出的第一个数最接近( B )
A. 1.7
B. 1.732
C. 1.75
D. 2
分析
当n=3时,solve1求出平方根整数为1
//模拟过程
n=3 l=0 r=3
//0<=3 进入循环
//第1次循环
mid=(l+r)/2=(0+3)/2=1 ,mid * mid =1 * 1=1<=3 条件满足 l=mid+1=1+1=2 r=3
//2<=3 条件满足
//第2次循环
mid=(l+r)/2=(2+3)/2=2, mid * mid =2 * 2 =4<=3 不满足,r=mid-1=2-1=1 l=2
//2<=1 条件不满足 退出循环
//返回 l-1 = 2 -1 =1k为10,执行10次 x = (x + n / x) / 2;
第1次 x=(1+3/1)/2=2
第2次 x=(2+3/2)/2=1.75
第3次 x=(1.75+3/1.75)/2=1.732
第4次 x=(1.732+3/1.732)/2=1.732
3/1.732 =1.732 所以后续计算约等于1.732所以选B
34.当输入为"256 11"时,输出的第一个数( A )
A. 等于16
B. 接近但小于16
C. 接近但大于16
D. 前三种情况都有可能
分析
当n=256时,solve1求出平方根整数为16
//模拟过程
n=256 l=0 r=256
//0<=256 进入循环
//第1次循环
mid=(l+r)/2=(0+256)/2=128 ,mid * mid =128 * 128<=256 条件不满足 r=mid-1=128-1=127 l=0
//0<=127 条件满足
//第2次循环
mid=(l+r)/2=(0+127)/2=63, mid * mid =63 * 63 <=256 条件不满足,r=mid-1=63-1=62 l=0
//0<=62 条件满足
//第3次循环
mid=(l+r)/2=(0+62)/2=31, mid * mid =31 * 31 <=256 条件不满足,r=mid-1=31-1=30 l=0
//0<=30 条件满足
//第4次循环
mid=(l+r)/2=(0+30)/2=15, mid * mid =15 * 15 =225 <=256 条件满足,l=mid+1=15+1=16 r=30
//16<=30 条件满足
//第5次循环
mid=(l+r)/2=(16+30)/2=24, mid * mid =24 * 24<=256 不满足,r=mid-1=24-1=2 l=16
//16<=23 条件满足
//第6次循环
mid=(l+r)/2=(16+23)/2=19, mid * mid =19 * 19<=256 不满足,r=mid-1=19-1=18 l=16
//16<=18条件满足
//第7次循环
mid=(l+r)/2=(16+18)/2=17, mid * mid =17 * 17<=256 不满足,r=mid-1=17-1=16 l=16
//16<=16条件满足
//第8次循环
mid=(l+r)/2=(16+16)/2=16, mid * mid =16 * 16<=256 条件满足,l=mid+1=16+1=17 r=16
//17<=16 条件不满足 退出循环
//返回 l-1 = 17 -1 =16k为11,执行11次 x = (x + n / x) / 2;
第1次 x=(16+256/16)/2=16
第2次 x=(16+256/16)/2=16
....
第11次 x=(16+256/16)/2=16所以选A