给你一个下标从 0 开始的整数数组 nums 。
一开始,所有下标都没有被标记。你可以执行以下操作任意次:
选择两个 互不相同且未标记 的下标 i 和 j ,满足 2 * nums[i] <= nums[j] ,标记下标 i 和 j 。
请你执行上述操作任意次,返回 nums 中最多可以标记的下标数目。
示例 1:
输入:nums = [3,5,2,4]
输出:2
解释:第一次操作中,选择 i = 2 和 j = 1 ,操作可以执行的原因是 2 * nums[2] <= nums[1] ,标记下标 2 和 1 。
没有其他更多可执行的操作,所以答案为 2 。
示例 2:
输入:nums = [9,2,5,4]
输出:4
解释:第一次操作中,选择 i = 3 和 j = 0 ,操作可以执行的原因是 2 * nums[3] <= nums[0] ,标记下标 3 和 0 。
第二次操作中,选择 i = 1 和 j = 2 ,操作可以执行的原因是 2 * nums[1] <= nums[2] ,标记下标 1 和 2 。
没有其他更多可执行的操作,所以答案为 4 。
示例 3:
输入:nums = [7,6,8]
输出:0
解释:没有任何可以执行的操作,所以答案为 0 。
提示:
1 <= nums.length <= 105
1 <= nums[i] <= 109
解题思路:
题目是找出两个 互不相同且未标记 的下标,一共能构成多少组
要求:1.互不相同且未标记
2.满足2 * nums[3] <= nums[0]
思路:
1.先数组排序,让数组变的有序
2.排序完后数组就变的有序了,使用双指针,左指针从0开始,右指针从1开始,那么就有了循环的依据(左指针最大是数组的长度的一半,右指针的数组长度,条件就是能组成的对数)
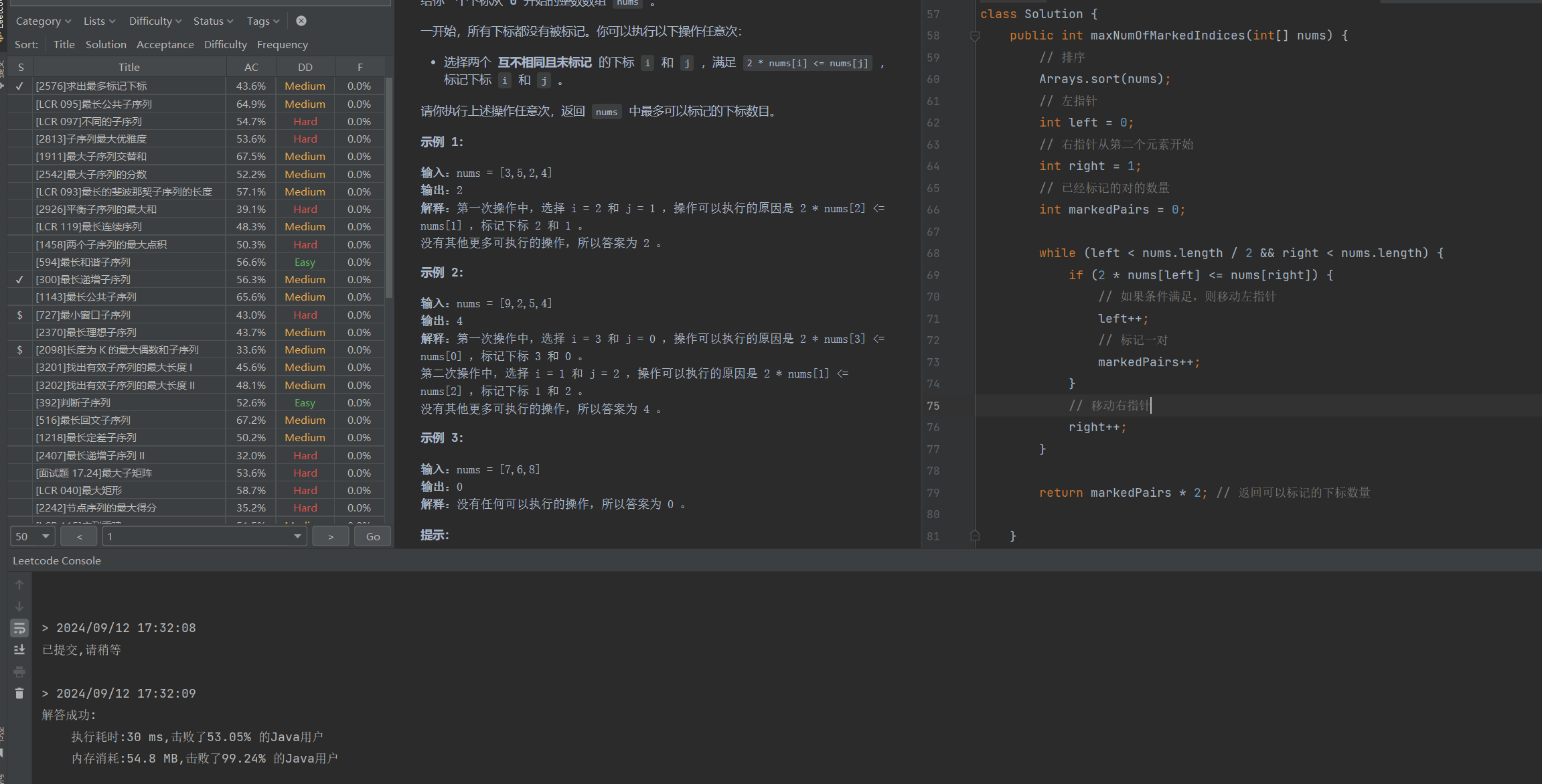
这里补充一点:因为数组是有序的,所以右指针右边的数一定大于左边的数,假设有对数组排序完是1,3,9....时,left = 0,right = 1时 满足2 * nums[1] <= nums[1]的条件,不用考虑nums[1]是否被标记,以为下标right 后面任何一个数都满足,循环条件 right < nums.length 不满足时,则循环也就结束了