[NOIP 2024 模拟2]数组操作
题意
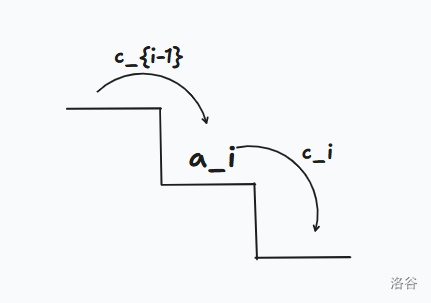
有 \(n + 2\) 个整数 \(a_0, a_1, . . . , a_n, a_{n+1}\),\(a_0 = a_{n+1} = 0\)。你需要做确切地 \(n\) 次操作,每次数组操作为以下形式: 选择一个整数 \(x\) 满足 \(a_x \ne 0\),使得 \(a_x = 0\),令 \(l=\max_{i<x,a_i=0} i,r=\min_{i>x,a_i=0} i\),此次操作的花费为 $\max(a_l, a_{l+1}+, . . . , a_{x−1}) + \max(a_{x+1}. . . , a_{r−1}, a_r) $牛币。 有多少不同的操作方式使得操作花费的牛币最少,两种操作不同当且仅当两种操 作的操作序列不同。 答案对 \(998244353\) 取模。
思路
发现把一个位置变成 \(0\) 后左右两部分就没有关系了,可以使用区间 dp。
定义 \(f_{i,j}\) 表示操作区间 \([i,j]\) 的最小代价,\(g_{i,j}\) 表示操作区间 \([i,j]\) 代价最小的方案数。
\(f_{i,j} = \min(f_{i,k-1}+f_{k+1,j}+\max_{i\le t<k}a_t+\max_{k< t\le j} a_t)\)
\(g_{i,j}=\sum_{k\rightarrow (i,j)} g_{i,k-1}\times g_{k+1,j} \times C_{j-i}^{k-i}\)
第一个转移方程显然。第二个转移方程的 \(C_{j-i}^{k-i}\) 表示这个区间还剩下 \(j-i\) 个操作(按顺序),分 \(k-i\) 个给左边,剩下的给右边,所以 \(C_{j-i}^{j-k}\) 也正确。可能会有疑问,只确定了哪些操作给左边,哪些操作给右边,但内部的顺序没有确定啊?实际上,虽然区间 dp 是从小区间合并成大区间,但实际操作时是从大区间分成小区间,这里只用确定哪些分给左边,哪些分给右边,它们内部的顺序它们自己分的时候会确定好。
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 998244353;
const int N = 2e3 + 5;
int n, a[N], pre[N], suf[N];
ll cnt[N][N], dp[N][N], c[N][N];
void solve() {cin >> n;for (int i = 1; i <= n; i ++) cin >> a[i];c[0][0] = 1;for (int i = 1; i <= n; i ++) {c[i][0] = 1;for (int j = 1; j <= n; j ++) {c[i][j] = c[i - 1][j] + c[i - 1][j - 1];c[i][j] %= mod;}}for (int i = 0; i <= n + 1; i ++) for (int j = 0; j <= n + 1; j ++) cnt[i][j] = 1;for (int k = 1; k <= n; k ++) {for (int i = 1; i <= n; i ++) {int j = i + k - 1;if (j > n) break;pre[i - 1] = 0, suf[j + 1] = 0;for (int t = i; t <= j; t ++) pre[t] = max(pre[t - 1], a[t]);for (int t = j; t >= i; t --) suf[t] = max(suf[t + 1], a[t]);dp[i][j] = 1e9, cnt[i][j] = 0;for (int t = i; t <= j; t ++) dp[i][j] = min(dp[i][j], dp[i][t - 1] + dp[t + 1][j] + pre[t - 1] + suf[t + 1]);for (int t = i; t <= j; t ++) if (dp[i][t - 1] + dp[t + 1][j] + pre[t - 1] + suf[t + 1] == dp[i][j]) cnt[i][j] += cnt[i][t - 1] * cnt[t + 1][j] % mod * c[j - i][j - t] % mod, cnt[i][j] %= mod;}}cout << cnt[1][n] << "\n";
}
signed main() {freopen("arr.in", "r", stdin);freopen("arr.out", "w", stdout);int Case = 1;
// cin >> Case;while (Case --)solve();return 0;
}