降维算法 0基础小白也能懂(附代码)
原文链接
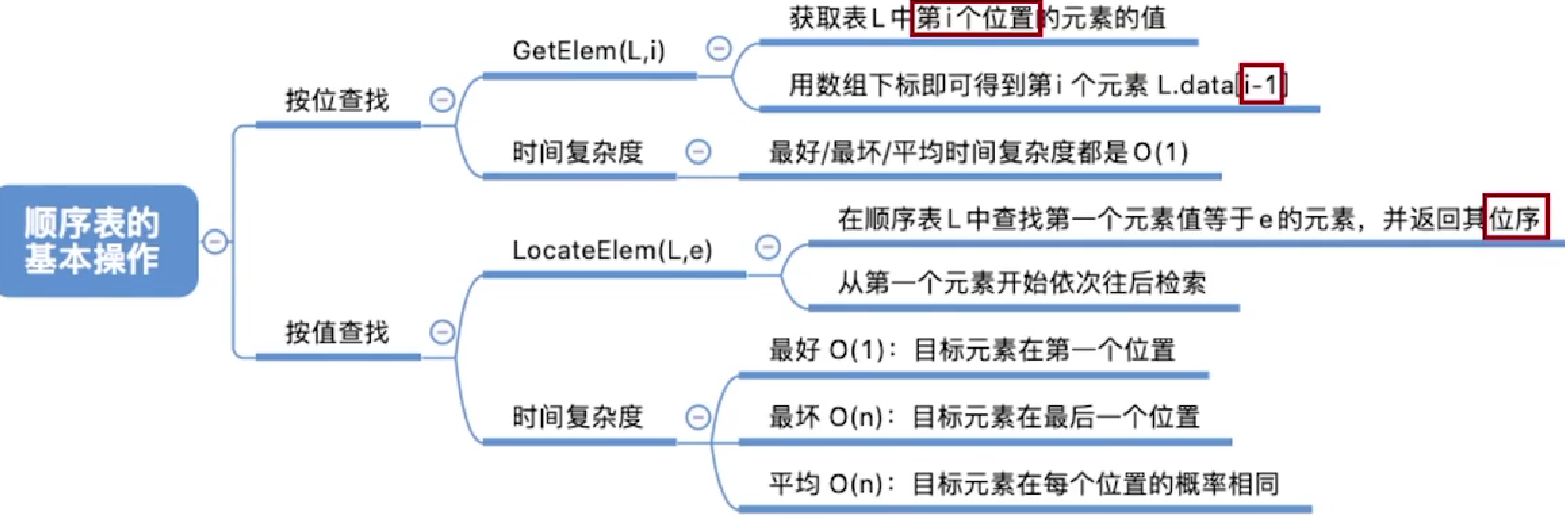
啥是降维算法
在互联网大数据场景下,我们经常需要面对高维数据,在对这些数据做分析和可视化的时候,我们通常会面对「高维」这个障碍。在数据挖掘和建模的过程中,高维数据也同样带来大的计算量,占据更多的资源,而且许多变量之间可能存在相关性,从而增加了分析与建模的复杂性。
我们希望找到一种方法,在对数据完成降维「压缩」的同时,尽量减少信息损失。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。机器学习中的降维算法就是这样的一类算法。
主成分分析(Principal Components Analysis,简称PCA)是最重要的数据降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。本篇我们来展开讲解一下这个算法。
PCA与最大可分性
对于\(X= \left[ \begin{matrix}x_1 \\x_2 \\\vdots\\x_n \\ \end{matrix} \right] ,X\in R^n\),我们希望\(X\)从\(n\)维降到\(n^{'}\)维,同时希望信息损失最少。比如,从\(n=2\)维降到\(n^{'}=1\)维
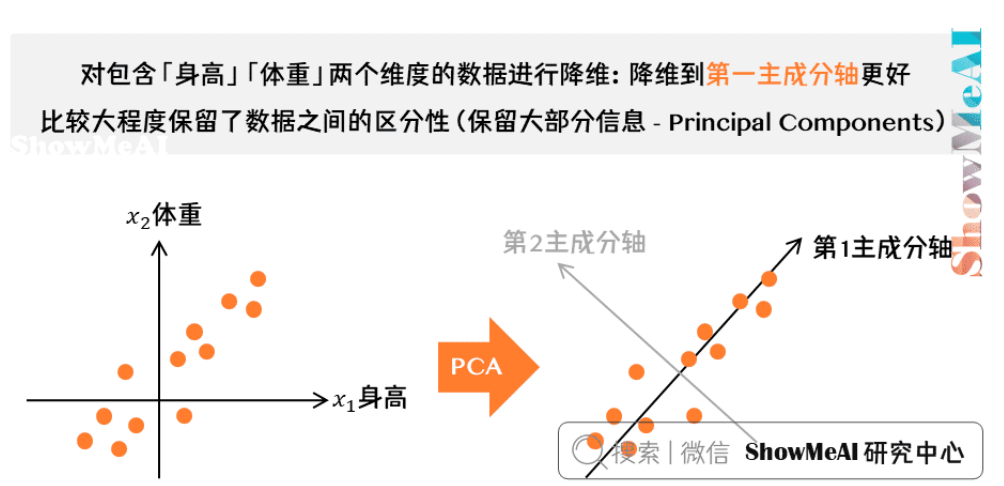
上图为一个典型的例子,假如我们要对一系列人的样本进行数据降维(每个样本包含「身高」「体重」两个维度)。右图我们既可以降维到第一主成分轴,也可以降维到第二主成分轴。
哪个主成分轴更优呢?从直观感觉上,我们会认为「第一主成分轴」优于「第二主成分轴」,因为它比较大程度保留了数据之间的区分性(保留大部分信息)。
对PCA算法而言,我们希望找到小于原数据维度的若干个投影坐标方向,把数据投影在这些方向,获得压缩的信息表示。下面我们就一步一步来推导一下 PCA 算法原理。
基变换
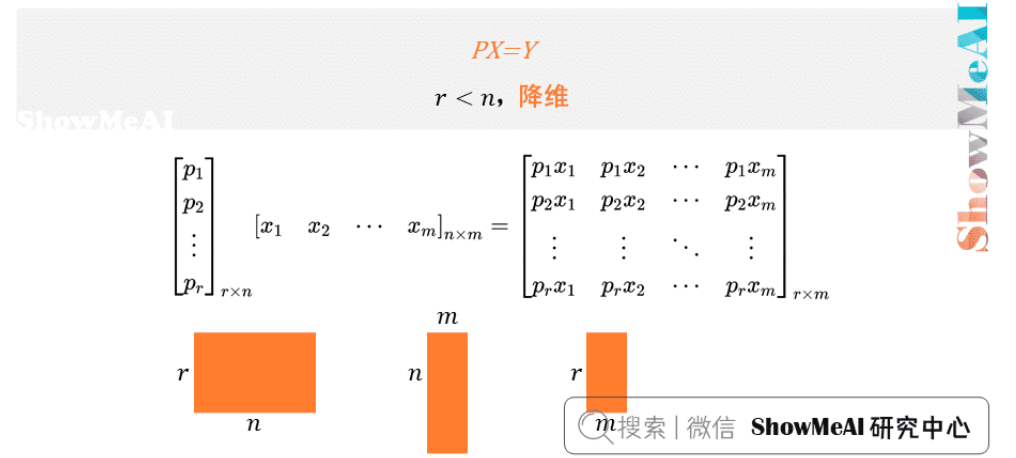

其实就是线性代数里面的矩阵相乘
方差
在本文的开始部分,我们提到了,降维的目的是希望压缩数据但信息损失最少,也就是说,我们希望投影后的数据尽可能分散开。在数学上,这种分散程度我们用「方差」来表达,方差越大,数据越分散。
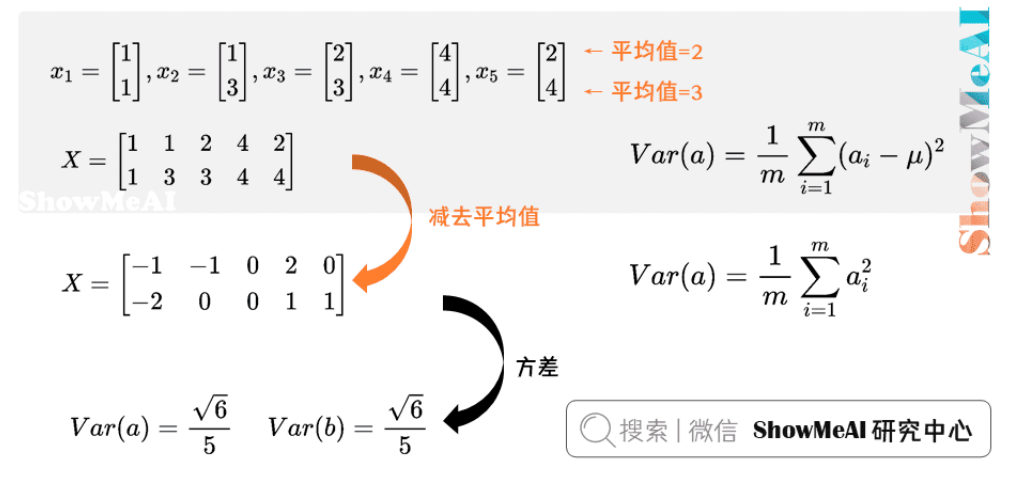
设第一个特征为\(a\),第二个特征为\(b\),则某个样本可以写作\(x_i=\left[ \begin{matrix} a \\b \\ \end{matrix} \right]\)
协方差
协方差(Covariance)在概率和统计学中用于衡量两个变量的总体误差。比如对于二维随机变量 \(x_i=\left[ \begin{matrix} a \\b \\ \end{matrix} \right]\),特征a,b除了自身的数学期望和方差,还需要讨论a,b之间互相关系的数学特征。
协方差 \(Cov=\frac{1}{m}\sum_{i=1}^ma_ib_i\)
当 \(Cov=0\)时,变量a,b完全独立,这也是我们希望达到的优化目标。方差是协方差的一种特殊情况,即当两个变量是相同的情况 。
协方差矩阵
对于\(n\)维随机变量,\(x_i=\left[ \begin{matrix}
x_1 \\
x_2 \\
\vdots \\
x_n\\
\end{matrix}
\right]
,C
=\left[
\begin{matrix}Var(x_1) & Cov(x_1,x_2) & \cdots & Cov(x_1,x_n) \\Cov(x_2,x_1) & Var(x_2) & \cdots & Cov(x_1,x_n) \\\vdots & \vdots & \ddots & \vdots \\Cov(x_n,x_1) & Cov(x_n,x_2) & \cdots & Var(x_n) \\
\end{matrix}
\right]
\)
我们可以看到,协方差矩阵是 n 行 n 列的对称矩阵,主对角线上是方差,而协对角线上是协方差。
那如果有 m 个样本的话,\(X=\left[ \begin{matrix} a_1 & a_2 &\cdots & a_m \\ b_1 & b_2 & \cdots & b_m \\ \end{matrix} \right]\)。对\(X\)做一些变换,用 \(X\) 乘以 \(X\) 的转置,并乘上系数 \(1/m\):
\(\frac{1}{m}XX^T=\frac{1}{m} \left[
\begin{matrix}
a_1 & a_2 &\cdots & a_m \\
b_1 & b_2 & \cdots & b_m \\
\end{matrix}
\right]\left[
\begin{matrix}
a_1 & b_1 \\
a_2 & b_2 \\
\vdots & \vdots \\
a_n & b_n
\end{matrix}
\right] ==\left[
\begin{matrix}
\frac{1}{m}\sum_{i=1}^ma_i^2 & \frac{1}{m}\sum_{i=1}^ma_ib_i \\
\frac{1}{m}\sum_{i=1}^ma_ib_i & \frac{1}{m}\sum_{i=1}^mb_i^2 \\
\end{matrix}
\right]
\)
这正是协方差矩阵!
协方差矩阵对角化
再回到我们的场景和目标:
-
现在我们有 m 个样本数据,每个样本有 n 个特征,那么设这些原始数据为 X,X 为 n 行 m 列的矩阵。
-
想要找到一个基 P ,使 \(Y_{r\times m}=P_{r\times n}X_{n\times m}\),其中 \(r<n\),达到降维的目的
设 \(X\) 的协方差矩阵为 \(C\),\(Y\) 的协方差矩阵为 \(D\),且\(Y=PX\) 。
我们的目标变为:对原始数据X做PCA后,得到的 Y 的协方差矩阵 D 的各个方向方差最大(数据的方差表示了数据在该方向上的分散程度,也可以看作是数据中蕴含的信息量。通过选择方差最大的方向,我们能够保留尽可能多的原始数据中的信息。),协方差为 0。
那么 C 与 D 是什么关系呢?
\(D=\frac{1}{m}YY^T=\frac{1}{m}(PX)(PX^T)=\frac{1}{m}PXX^TP^T=PCP^T\)
到这里就可以了,可以发现\(D\)和\(C\)是通过\(P\)相联系的,同时呢,我们希望它是对角矩阵。这是因为对角矩阵意味着各个维度之间的协方差为 0,也就是说,新的主成分是相互独立的。这正是 PCA 的目标:找到这样一个变换,使得在新坐标系下,各个方向上数据的方差最大且相互独立。
之前我们说过,协方差矩阵\(C\)是一个是对称矩阵,实对称矩阵具有一些非常有用的性质:
正交特性:实对称矩阵的不同特征值对应的特征向量必然正交。
特征向量的线性无关性:对于具有相同特征值的特征向量,存在多个线性无关的特征向量,并且这些特征向量可以正交化。
由上面两条可知,一个\(n\)行\(n\)列的实对称矩阵一定可以找到\(n\)个单位正交特征向量,设这\(n\)个特征向量为\(e_1,e_2,...,e_n\),我们将其按列组成矩阵:\(E=[e_1 e_2 ... e_n]\)
则对协方差矩阵\(C\)有如下结论:
\(E^TCE=\)\(\Lambda = \begin{pmatrix}
\lambda_1 & 0 & 0 & \dots & 0 \\
0 & \lambda_2 & 0 & \dots & 0 \\
0 & 0 & \lambda_3 & \dots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \dots & \lambda_n
\end{pmatrix}\),其对角元素为各特征向量对应的特征值(可能有重复)。
这里也就是\(E^T=P\),这样\(D\)就对角了。
PCA算法思路整理

代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs# 定义PCA算法
def PCA(X, num_components):# 数据中心化X_meaned = X - np.mean(X, axis=0)# 计算协方差矩阵covariance_matrix = np.cov(X_meaned, rowvar=False)# 计算协方差矩阵的特征值和特征向量eigen_values, eigen_vectors = np.linalg.eigh(covariance_matrix)# 按照特征值从大到小排序sorted_index = np.argsort(eigen_values)[::-1]sorted_eigenvalue = eigen_values[sorted_index]sorted_eigenvectors = eigen_vectors[:, sorted_index]# 选择前num_components个特征向量eigenvector_subset = sorted_eigenvectors[:, 0:num_components]# 将数据投影到这些特征向量上X_reduced = np.dot(X_meaned, eigenvector_subset)return X_reduced# 生成几个聚类的三维数据集
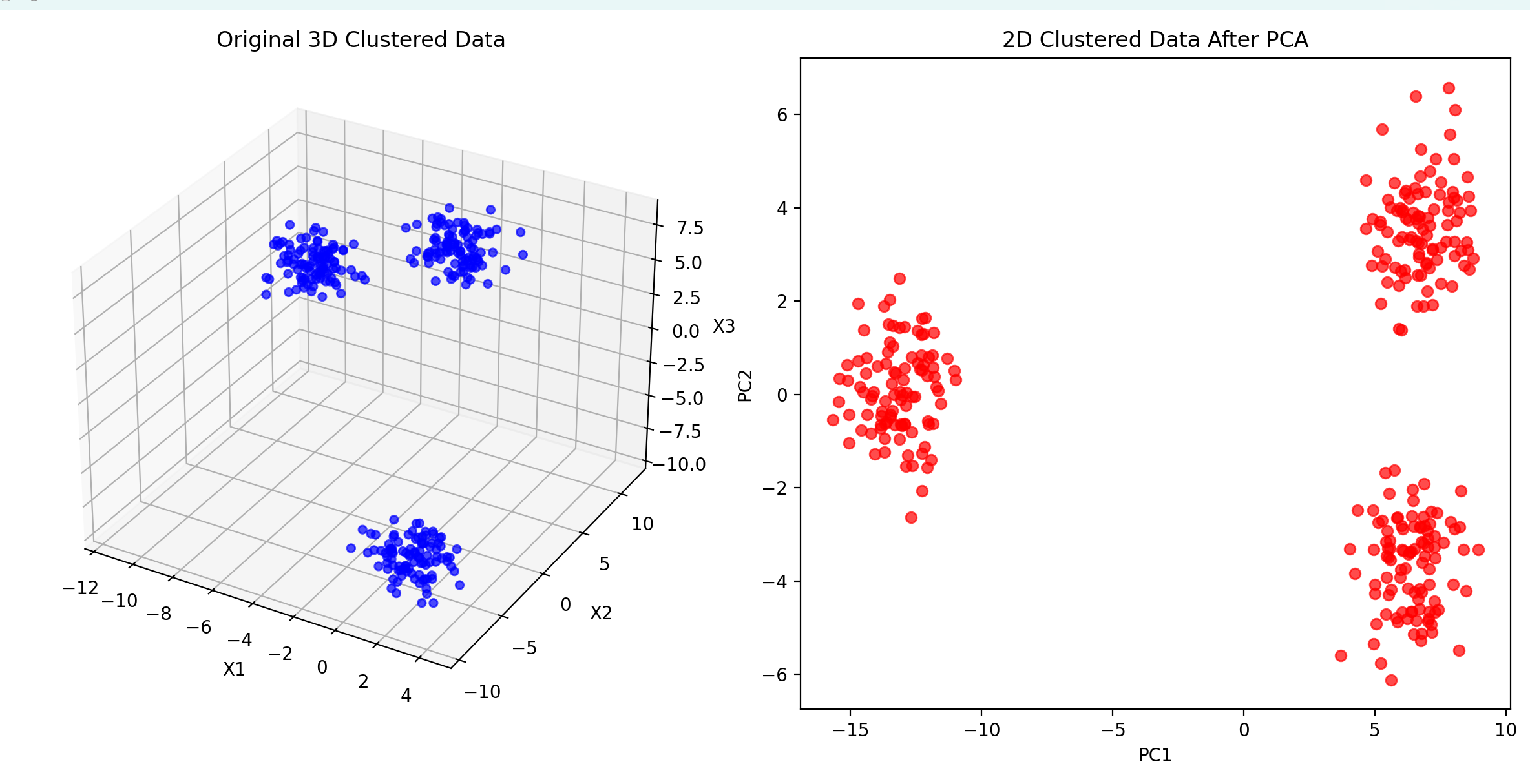
X, _ = make_blobs(n_samples=300, centers=3, n_features=3, cluster_std=1.0, random_state=42)# 使用PCA将三维数据降维到二维
X_reduced = PCA(X, 2)# 绘制三维原始数据和二维降维数据
fig = plt.figure(figsize=(12, 6))# 三维原始数据
ax1 = fig.add_subplot(121, projection='3d')
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], color='blue', alpha=0.7)
ax1.set_title('Original 3D Clustered Data')
ax1.set_xlabel('X1')
ax1.set_ylabel('X2')
ax1.set_zlabel('X3')# 二维降维数据
ax2 = fig.add_subplot(122)
ax2.scatter(X_reduced[:, 0], X_reduced[:, 1], color='red', alpha=0.7)
ax2.set_title('2D Clustered Data After PCA')
ax2.set_xlabel('PC1')
ax2.set_ylabel('PC2')plt.tight_layout()
plt.show()
结果如下