前言
计数加训!!!!
以下问题都是数数。
一些纯组合问题
插板法
例 1
求 $\sum_{i=1}^kx_i=n$ 的解的组数,其中 $x_i\in \mathbb{N^+}$ 且 $x_i\ge a_i$。
考虑令 $x_i'=x_i-a_i+1\ge 1$,于是有 $\sum_{i=1}^k x_i'=n-k+\sum a_i$,于是答案为
$$n-k+\sum a_i-1\choose k-1$$
例 2
从 $1\dots n$ 中选 $k$ 个数,求 $k$ 个数两两不相邻的方案数。
我们强制选上 $a_{k+1}=n+1$,考虑这 $(k+1)$ 个数形成的差分数组 $d_1\dots d_{k+1}$,需要满足 $d_1,d_{k+1}\ge 1,d_{2\dots k}\ge 2,\sum d=n+1$。
于是答案为 ${n+1-k-1+2k-1\choose k}={n+k-1\choose k}$。
不知道叫什么1
从 $1\dots n$ 中选 $m$ 个数,求所有方案选出数的和之和。
考虑总方案数共有 $n\choose m$ 种,对于一个数 $i$,它在 $\dfrac{n\choose m}{2}$ 种方案中被选中,因此答案为:
$$\sum_{i=1}^n\dfrac{n\choose m}{2}i={n\choose m}\sum_{i=1}^n i=\dfrac{n(n+1)}{2}{n\choose m}$$
组合数的前缀和
从 $n$ 个物品中选至多 $m$ 个,求方案数。
$$\text{令}S(n,m)=\sum_{i=0}^m{n\choose i}$$
对于 $m$ 为定值的情况,考虑递推:
$$
\begin{aligned}
&\ \ \ \ S(n,m)-S(n-1,m)\
&=\sum_{i=0}^m{n\choose i}-\sum_{i=0}^m{n-1\choose i}\
&=\sum_{i=0}^m({n-1\choose i}+{n-1\choose i-1})-\sum_{i=0}^m{n-1\choose i}\
&=\sum_{i=0}^m {n-1\choose i-1}\
&=S(n-1,m)-{n-1\choose m}\
&\implies S(n,m)=2S(n-1,m)-{n-1\choose m}
\end{aligned}
$$
$(-1)^i$ 与组合数
我们很久以前就学过:
$\sum_{i=0}^n (-1)^i {n\choose i}=[n=0]$
$\dfrac{1}{y}\sum_{j\ge0}(-\dfrac{x}{y})^j=\dfrac{1}{y}\dfrac{1}{1+\dfrac{x}{y}}(|\dfrac{x}{y}|<1)$
我们现在魔怔一点,考虑以下这个式子:
$$\sum_{i=0}n(-1)i{n\choose i}\dfrac{1}{Ai+B}$$
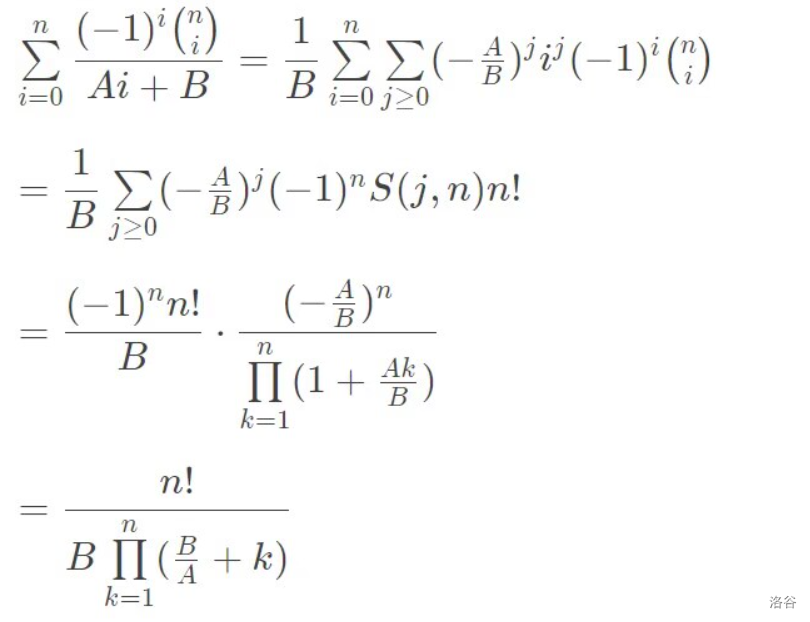
???
$$k\sum_{i=0}{k-1}(-1)i\dfrac{1}{i+2}{k-1\choose i}=\dfrac{1}{k+1}$$
排序等 trick 解除后效性
例 1
给出数组 $a$,求有多少个数组 $x$ 满足,$x_i\le a_i$,且 $x_i$ 两两不同。
考虑先把 $a$ 数组升序排序,前面的选择对后面就没有影响了,然后 $x_i$ 就一共有 $(a_i-i+1)$ 种选法。
例 2
[AGC023E] Inversions
延续例 1 的思路,我们从小到大加入 $p_i$。则合法方案数为 $tot=\prod(a_i-rk_i+1)$,记 $b_i=a_i-rk_i+1$。
考虑一对 $(i,j)$ 对答案的贡献,分情况讨论,不妨令 $j<i$。
-
$rk_j< rk_i:$ 此时若要形成逆序对,则 $p_i<a_j$。因此,如果我们把 $a_i$ 变成 $a_j$,此时合法的排列中,一半 $(i,j)$ 是顺序对,另一半是逆序对。所以我们此时只需要数合法排列数。
考虑 $a_i$ 变成 $a_j$ 对 $\prod b$ 的影响。首先是对于所有的 $k$ 满足 $rk_k\in(rk_j,rk_i)$,$b_k$ 都要 $-1$,然后是 $b_i$ 要变成 $(b_j-1)$。因此这对 $(i,j)$ 的贡献为
$$\dfrac{tot(b_j-1)}{2b_i}\prod_{k}\dfrac{b_k-1}{b_k}$$
-
$rk_j>rk_i:$ 此时我们计算 $(i,j)$ 形成的顺序对个数,再用总方案数减去即可。同样地,把 $a_j$ 变成 $a_i$,式子是
$$\dfrac{tot(b_i-1)}{2b_j}\prod_{k}\dfrac{b_k-1}{b_k}$$
发现这不就是单点修改区间乘区间求和吗,线段树优化即可。
例 3
有 $n$ 个数 $a_1\dots a_n$,你要把它们划分成 $m$ 个子序列,要求第 $i$ 个子序列里的数都 $\ge b_i(i\in[1,m])$,第 $i$ 个子序列的长度为 $len_i$,求方案数。
考虑把 $a,b$ 合起来从大到小排序,然后从左到右扫。考虑到第 $i$ 个位置,它是 $b$ 中的数,假设前面有 $A$ 个 $a$ 中的数,前面 $len$ 的和是 $L$。则剩下划分给它的数有 $(A-L)$ 个,方案数为 ${A-L\choose len_i}$。
Min-Max 容斥
式子:
$$
\min(S)=\sum_{T\ne \emptyset,T\subseteq S}(-1)^{|T|-1}\max(T)
$$
其实可以用容斥来理解,$S$ 表示不小于 $n$ 的正整数集合,则子集的交就是取 $\max$,子集的并就是取 $\min$,然后就发现跟容斥一模一样。
当然,关于容斥系数,如果记不住,举个例子手玩即可。
Min-Max 容斥常用于解决 $\min/\max$ 其中一个计算极度困难的问题。
例 1
[AGC038E] Gachapon
令 $A=\sum_{i=1}^n A_i,B=\sum_{i=1}^n B_i$。
如果我们对每个数考虑生成的最晚步数 $t$,那全部生成到 $\ge B_i$ 次的期望步数相当于生成 $t$ 最大的数的期望步数,发现这个不好算。套用 Min-Max 容斥的话,$\min(T)$ 的含义就是至少有一个数达到了 $B_i$ 的期望步数。
$$
E(\max(S))=\sum_{T\ne\emptyset\subseteq S}(-1)^{|T|-1}E(\min(T))
$$
这里外面可以套一层 $E$ 的原因是期望的线性性。
然后我们要想怎么算 $E(\min(T))$。
先算出随到一次 $T$ 内的数的期望步数,显然是 $w=\dfrac{A}{\sum_{i\in T}A_i}$,于是我们不需再考虑集合外的元素。
然后期望转概率:
$$E(\min(T))=\sum_{k=1}P(x=k)k=\sum_{k=1}P(x\ge k)$$
其中 $P(x=k)$ 表示 $k$ 步内,至少有一个数达到了 $B_i$ 的概率,上界懒得想了,最后 DP 过程中会自动处理掉,超过的部分自动会变成 $0$。
考虑 $P(x\ge k)$ 等价于在 $(k-1)$ 步内任何一个数都没达到 $B_i$,于是我们只需要算出 $(k-1)$ 步内一个数都没达到 $B_i$ 的概率。
下面令 $k\gets (k-1)$。枚举每个数随到的次数 $c_i$,满足 $c_i<b_i,\sum c_i=k$,那当前局面的方案数为:
$$
\prod_{i\in T}{k-\sum_{j=0}^{j-1}c_j\choose c_i}=\dfrac{k!}{\prod_{i\in T}c_i!}
$$
每种方案的概率为:
$$
\prod_{i\in T}(\dfrac{A_i}{\sum_{j\in T}A_j})^{c_i}
$$
整理:
$$
\begin{aligned}
&\dfrac{k!}{\prod_{i\in T}c_i!}\prod_{i\in T}(\dfrac{A_i}{\sum_{j\in T}A_j})^{c_i}\
=&\dfrac{k!}{(\sum_{j\in T}A_j)^k}\prod_{i\in T}\dfrac{A_i^{c_i}}{c_i!}\
\end{aligned}
$$
带回原式,别忘了把 $w$ 乘回来:
$$
\begin{aligned}
ans=&\sum_{T\ne\emptyset\subseteq S}(-1)^{|T|-1}E(\min(T))\
=&\sum_{T\ne\emptyset\subseteq S}(-1)^{|T|-1}w\sum_{k=0}P(x\ge k)\
=&{\color{red}A\sum_{T\ne\emptyset\subseteq S}\sum_{k=0}\dfrac{k!}{(\sum_{j\in T}A_j){k+1}}}(-1)\prod_{i\in T}\dfrac{A_i^{c_i}}{c_i!}
\end{aligned}
$$
这么一坨东西,咋算?考虑用背包来跑这个容斥,具体地,设 $f[i][j][k]$ 表示考虑了前 $i$ 个物品,$\sum A=j,\sum c=k$ 的这一坨式子,那么红色部分可以最后加起来/乘进去,转移方程为:
$$
f[i][j][k]\gets f[i-1][j][k]-\sum_{c_i=0}^{\min(b_i-1,k)}f[i-1][j-A_i][k-c_i]\times \dfrac{A_i^{c_i}}{c_i!}
$$
最后答案就是 $A\sum_{i=0}A\sum_{j=0}Bf[n][i][j]\dfrac{j!}{i^{j+1}}$。
复杂度 $\mathcal O(n\sum A\sum B)$。
组合意义优化
目前的感觉是,当题目要求计数的东西很莫名其妙的时候,一般需要考虑其组合意义。
然后经典用途是优化连乘!!!!!!
例 1
Cookie Distribution
想法是,$\prod_{i=1}^nc_i$ 这个东西不好记到状态里,但是这个等同于每个人从获得的糖果里选出一个的方案数。
题里说再乘上那一坨,就是问所有情况下的方案数之和。
因此设 $f_{i,j}$ 表示考虑到前 $i$ 天,已经有 $j$ 个人选出了糖果的方案数。
转移枚举 $t$ 表示这天发到的 $t$ 个人选出了糖果,有
$$f_{i,j}\gets f_{i-1,j-t}{n-(j-t)\choose t}{n-t\choose a_i-t}$$
例 2
[AGC013E] Placing Squares
尝试 DP,设 $f_{i}$ 表示考虑了前 $i$ 个格子的方案数,转移是
$$
f_i=\sum_{j<i,j\notin S}f_j\times (i-j)^2
$$
感觉到这里就很难转移了,如果是加号还可以矩阵乘法,但是这个乘号非常困难。
一切都是因为 $\prod a_i^2$ 这个东西很神秘,所以想一下它的组合意义。
如果划分出的这一段边长为 $a_i$,我们在其中放一个猫猫球和一个喵喵球,允许它们重叠在同一个位置上,那方案数就恰好是 $a_i^2$。
于是我们设 $f_{i,j}$ 表示考虑到前 $i$ 个位置,距离上次隔开的地方已经放了 $j$ 个球($j\in[0,2]$)的方案数。
对于允许隔开的地方,有转移:
$$
f_{i,0}=f_{i-1,0}+f_{i-1,2}\
f_{i,1}=2f_{i-1,0}+f_{i-1,1}+2f_{i-1,2}\
f_{i,2}=f_{i-1,0}+f_{i-1,1}+2f_{i-1,2}\
$$
对于不允许隔开的地方,有转移:
$$
f_{i,0}=f_{i-1,0}\
f_{i,1}=2f_{i-1,0}+f_{i-1,1}\
f_{i,2}=f_{i-1,0}+f_{i-1,1}+f_{i-1,2}\
$$
然后发现可以矩阵快速幂。
例 3
[ARC182C] Sum of Number of Divisors of Product
看到连乘为啥又没想到组合意义???
首先 $d(n)=\prod p_i^{k_i}$,而 $16$ 以内的质数只有 $6$ 个,因此可以考虑设计指数级的状态进行 DP,看到 $n$ 很大,优先考虑矩阵快速幂。
我们要求的就是所有序列的 $\prod$ 之和,考虑连乘的组合意义:对每个 $p_i$,从 $k_i$ 个数中选择一个(可以不选)的方案数。
发现问题一下子明朗了。设 $f_{i,mask}$ 表示考虑到序列中前 $i$ 个数,$mask$ 中的质因子已经选好了的方案数总和,转移枚举 $i$ 这一位填的数 $x$,考察 $x$ 的质因数分解,其中每个质因数都可以在 $x$ 这里选出,也可以在之前选出,若在 $x$ 选出,且 $x$ 能分解出多个同样的质因子,还可以决定选哪一个。
然后矩阵快速幂加速转移即可。
期望相关
假如有一种随机事件,每次发生的概率为 $p$,且不发生对发生没有影响,此时发生它的期望步数为 $\dfrac{1}{p}$。
例 1
FAVDICE - Favorite Dice
假如已经投出了 $n$ 个数中的 $x$ 个,那么投出其余 $(n-x+1)$ 个数的概率就是 $\dfrac{n-x+1}{n}$,期望步数就是 $\dfrac{n}{n-x+1}$,于是可以递推。
期望的等价转化
有一种类似树上删点,问期望几次删空的模型,可以采用以下套路:
首先,转化为从 $n!$ 个操作序列中随机选一个,如果当前操作的点被删过就 continue。
然后,根据期望的线性性,可以求对每个点操作次数的期望再相加。
考察一个点被操作的充要条件,对应到操作序列上计算概率,或者转计数。
例 1
CF280C Game on Tree
应用前面的套路,点 $u$ 被操作当且仅当它在操作序列中的位置在所有祖先之前,概率为 $\dfrac{1}{dep_u}$,期望数值上等于概率。
例 2
[ARC150D] Removing Gacha
首先可以转化为,随机选择树上一个点,但是如果它到根的点都被选过就不算次数。
同样拆成每个点的期望操作次数求和,把点 $u$ 到根这条链提出来考虑,可以用 favdice 那个题的做法算出这条链被填满的期望步数(注意这个步数并不等于次数),每步投到 $x$ 的概率都是 $\dfrac{1}{dep_x}$。
例 3
[ARC165E] Random Isolation
格路计数与反射容斥
格路计数
现在有一张二维的网格,你初始在 $(0,0)$,每次只能向上或者向右走一步,你要走到 $(n,m)$,问方案数。
考虑你一共要走 $(n+m)$ 步,这里面有 $n$ 步是向右的,于是方案数为 $n+m\choose n$。
反射
现在我们规定,有一条直线 $A:y=x+a$ 不能经过。
考虑每一条碰到 $A$ 的路径,从第一次碰到之后,把向上和向右翻转过来,得到一条新路径,这条路径的终点是 $(m-a,n+a)$,称这种操作为一次反射。
不难发现,所有到 $(m-a,n+a)$ 的路径都唯一对应一条到 $(n,m)$ 且经过了 $A$ 的路径,于是答案为 ${n+m\choose n}-{n+m\choose m-a}$。
反射容斥
如果再规定一条 $B:y=x+b$ 不能经过呢?
不妨令 $a>b$,然后很直接的想法就是,总方案数 $-$ 经过 $A$ 的方案数 $-$ 经过 $B$ 的方案数 $+$ 经过 $A$ 又经过 $B$ 的方案数。
两个都经过的方案数咋算?
朴素想法肯定是碰到一次直线就反射一次。
我们把一次终点关于 $A$ 的反射记为 $a$,关于 $B$ 的反射记为 $b$,于是我们可以把反射路径用一个含有 $a,b$ 的字符串表示出来。因为前面我们发现,连续经过同一条直线只需要反射一次,所以我们的字符串一定形如 $aba\dots$ 或 $bab\dots$。
然后我们把到反射序列 $S$ 得到的终点的方案数记作 $C(S)$,把严格按照反射路径走的方案数记作 $R(S)$,把以 $S$ 作为后缀的字符串集合记作 $suf(S)$
。
考虑 $C(a)$ 到底计算了什么,实际上,$C(a)=\sum_{S\in suf(a)\cup suf(ab)}R(S)$,也就是说,它计算的是所有以 $a$ 或 $ab$ 为后缀的 $S$ 的 $R(S)$。
于是我们可以审视刚刚的“$-$ 经过 $A$ 的方案数 $-$ 经过 $B$ 的方案数”,它写成反射序列的形式就是 $-C(a)-C(b)$,实际上减去的是所有以 $a,ab,b,ba$ 为后缀的 $S$ 的 $R(S)$。
但是我们只需要 $S\in suf(a)\cup suf(b)$ 的 $R(S)$。所以我们再加上 $C(ab)$ 和 $C(ba)$,发现我们又算多了 $R(S),S\in suf(aba)\cup suf(bab)$,于是再递归下去即可,复杂度 $\mathcal O(\dfrac{n+m}{a-b})$。
zhapian
如果再规定一条 $C:y=x+c$ 不能经过呢?
容易发现有用的直线只有最多两条。
应用
一般要发掘组合意义,把 DP 的式子对应到网格图上,然后反射的思想应该可以推广...?
例 1
P3266 [JLOI2015] 骗我呢
首先发现每一行有 $m$ 个数,值域为 $[0,m]$,然后题目又要求每一行单调递增,所以一行只有 $[0,m]$ 中的一个数没有出现。
于是可以设 $f_{i,j}$ 表示考虑了前 $i$ 行,第 $i$ 行没有填的数是 $j$ 的方案数。
另一个限制翻译过来讲就是第 $i$ 行没出现的数比上一行的最多小 $1$。
转移 $f_{i,j}=\sum_{k\le j+1} f_{i-1,k}$。
设 $g_{i,j}=\sum_{k\le j}f_{i,k}$,从转移 $f$ 变成转移 $g$:
$$f_{i,j}=g_{i-1,j+1}\g_{i,j}=f_{i,j}+g_{i,j-1}\ \implies g_{i,j}=g_{i-1,j+1}+g_{i,j-1}$$
答案就是 $g_{n,m}$。
不难发现,$g_{i,j}$ 代表从 $(0,0)$ 出发,每次可以向右下或者向上走一步,横纵坐标不能 $<0$,问方案数。
这个右下很烦,我们不妨令 $(x,y)\gets (x,y+x)$,然后就变成了刚刚的问题,不能经过的两条直线为 $y=x-1$ 和 $y=x+m+2$。
容斥
理解了容斥和各种反演的原理之后,麻烦就在于判断何时使用容斥以及对什么容斥,感觉这个只能加训。然后容斥常常搭配其他技巧,需要比较强大的 counting 基础。
例 1
CF1799G Count Voting
设一个组的大小为 $A_i$。
容斥,第 $t$ 组钦定有 $k_t$ 张票是自己组投的。
考虑第 $i$ 个人的 $c_i$ 张票里有 $d_i$ 张是自己组投的,总方案数为 $$$$
转移枚举第 $i$ 组有 $k$ 个人给自己组投票。
例 2
说点闲话,考虑这样一个问题:
有一个长度为 $n$ 的排列,其中第 $i$ 个数的值域为 $[l_i,r_i]$,求方案数。
我以为这个是简单组合问题,想了一年,直到遇见这个它的超级弱化版,竟然是 agc f。
[AGC036F] Square Constraints
先考虑值域为 $[1,r_i]$ 的问题。显然可以把所有数按照 $r_i$ 从小到大排序。答案就是 $\prod{(r_i-i+1)}$。
发现多了下界的限制,考虑容斥。钦定一些数字必须小于 $l_i$,则它们的值域变为 $[1,l_i-1]$。
然后你发现排名很难维护了。但是本题有两个重要的性质,即区间的左右端点单调递增。以及在去掉所有 $l_i=0$ 的位置后,$\min{r_i}>\max{l_i}$。
因此,我们先改为按照左端点排序。对于 $i$ 这个位置,如果选择 $r_i$ 作为上界,则它的排名应当是 $i+(\text{i 后面所有选择} $ $l_i-1$ $ \text{作为上界的位置数量})$;如果选择 $(l_i-1)$ 作为上界,它的排名应当是 $(\text{i 前面所有选择} $ $l_i-1$ $ \text{作为上界的位置数量})+1$。
接下来把去掉的位置插回去一起排序,发现因为它们一定选择了 $r$,所以新的排名也是简单的。
于是先枚举钦定 $k$ 个位置选择 $l-1$ 作为上界,设 $f_{i,j}$ 表示考虑了前 $i$ 个位置,已经有 $j$ 个位置选择了 $l-1$ 作为上界的方案数即可解决。