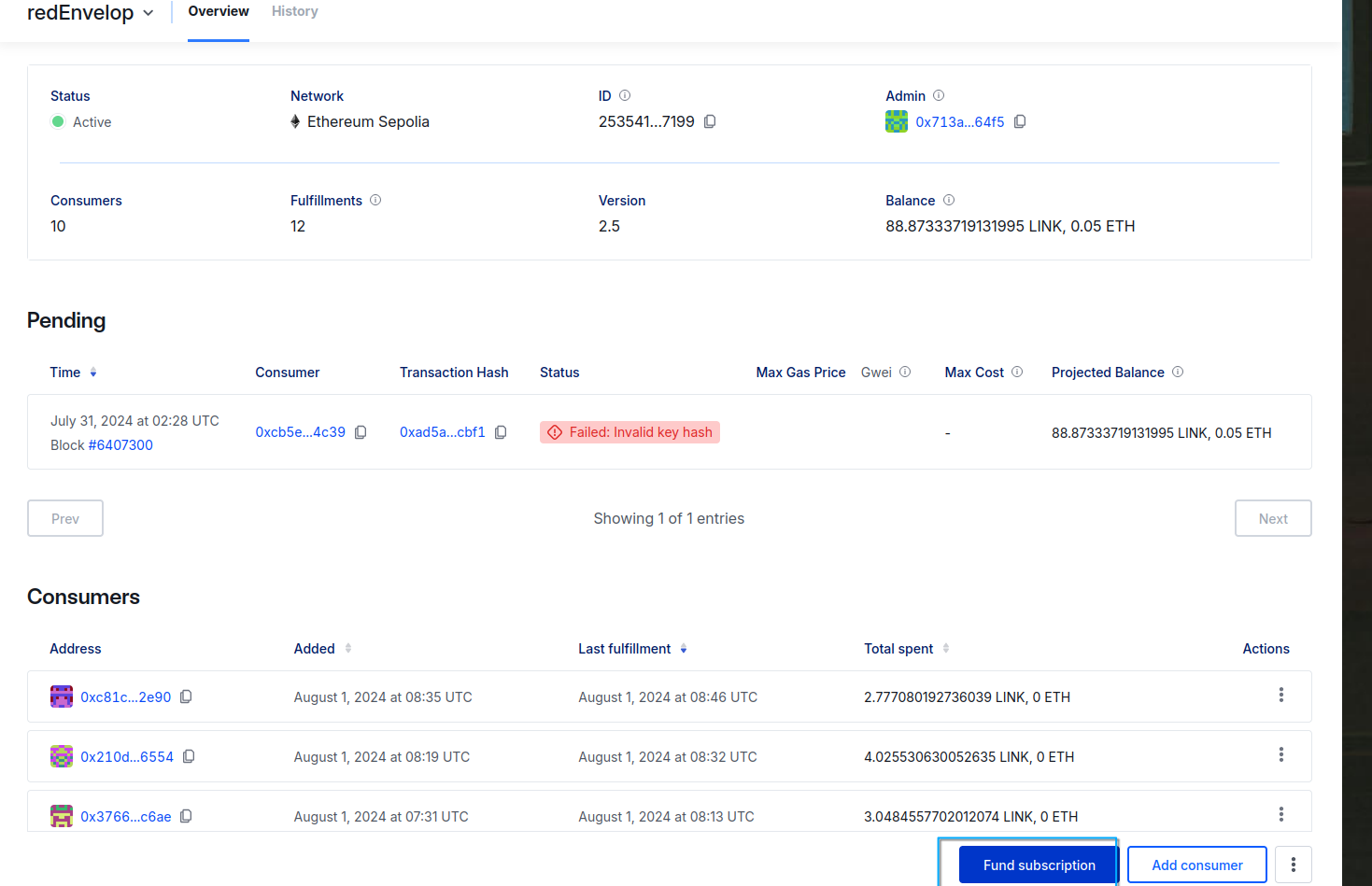
模拟赛 T3,去医院了没打,但是感觉很好玩。
首先有一个显然的 \(O(nk^2)\),设 \(f_{i,j}\) 表示前 \(i\) 个拼出长度为 \(j\) 的最小字典序串,很遗憾的是空间和时间都存不下。
有个优化是可以对后缀跑一边背包求出 \(g_{i,j}\) 表示后缀能否拼出长度为 \(j\) 的串,只记录有用的位置。
考虑优化,对于字符串问题找找关系,思考如何确定两个串的大小关系:只要出现一位不同即可。
也就是对于两个可行的状态 \(f_{i,j},f_{i,k},j < k\),若 \(f_{i,j}\) 与 \(f_{i,k}\) 已经确定至少一位不同,就可以扔掉劣的那个状态,换句话说这两个状态同时存在一定满足 \(f_{i,j}\) 为 \(f_{i,k}\) 的前缀。
所以对于一个 \(i\) 只需要存一个串就可以了,空间降为 \(O(nk)\)。
进一步,思考刚刚得到的结论,只需要把所有不满足的状态全部扔掉即可维护当前答案。
现在需要的是快速比较两个串的字典序,这个串是由 \(i-1\) 的答案的一段前缀和 \(i\) 的整个串(或没有)拼起来,只需要快速支持求 LCP 即可。
不会 Z 函数,写的 SA,复杂度 \(O(nk \log k)\)。
#include <bits/stdc++.h>
using namespace std;#define QwQ01AwA return 0
#define ll long long
#define debug(x) cerr << #x << " = " << x << '\n'
#define look_time cerr << 1.0 * clock() / CLOCKS_PER_SEC << '\n'
template <typename T> void ckmax(T &x, const T y) {x = max(x, y);}
template <typename T> void ckmin(T &x, const T y) {x = min(x, y);}namespace SA {const int N = 2e4 + 33;int rk[N], sa[N], oldrk[N << 1], id[N], cnt[N], st[15][N], lg[N];void build(int *w, int n) {int m = 27;for (int i = 0; i <= m; i++) cnt[i] = 0;for (int i = 1; i <= n; i++) rk[i] = w[i], cnt[rk[i]]++;for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];for (int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;for (int w = 1, c = 0, tot = 0; ; w *= 2, m = c, tot = c = 0) {for (int i = n; i > n - w; i--) id[++tot] = i;for (int i = 1; i <= n; i++) if (sa[i] > w) id[++tot] = sa[i] - w;for (int i = 0; i <= m; i++) cnt[i] = 0;for (int i = 1; i <= n; i++) oldrk[i] = rk[id[i]], cnt[oldrk[i]]++;for (int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];for (int i = n; i >= 1; i--) sa[cnt[oldrk[i]]--] = id[i], oldrk[i] = rk[i];#define cmp(u, v) (oldrk[u] == oldrk[v] && oldrk[u + w] == oldrk[v + w])rk[sa[1]] = ++c;for (int i = 2; i <= n; i++) {if (!cmp(sa[i], sa[i - 1])) c++;rk[sa[i]] = c;}if (c == n) break;}for (int i = 1, k = 0; i <= n; i++) {if (i != 1) lg[i] = lg[i >> 1] + 1;if (rk[i] == 1) continue;int j = sa[rk[i] - 1];if (k) k--;while (max(i, j) + k <= n && w[i + k] == w[j + k]) k++;st[0][rk[i]] = k;}for (int j = 1; j <= lg[n]; j++) {for (int i = 1; i + (1 << j) - 1 <= n; i++) {st[j][i] = min(st[j - 1][i], st[j - 1][i + (1 << (j - 1))]);}}for (int i = 1; i <= n; i++) oldrk[i] = 0;}int query(int l, int r) {// assert(l != r);l = rk[l], r = rk[r];if (l > r) swap(l, r);l++;int k = lg[r - l + 1];return min(st[k][l], st[k][r - (1 << k) + 1]);}
}
const int N = 2005;
const int M = 10005;
int n, k;
string s[N], t[N];
bitset <M> suf[N], f[N];
pair <int, int> stk[M]; int top;
int w[M * 2];signed main() {ios::sync_with_stdio(0);cin.tie(0);cin >> n >> k;for (int i = 1; i <= n; i++) cin >> s[i];suf[n + 1].set(0);for (int i = n; i >= 1; i--) suf[i] = suf[i + 1] | (suf[i + 1] << s[i].size());t[1] = " " + s[1], f[1][0] = f[1][s[1].size()] = 1;for (int i = 2; i <= n; i++) {int len = s[i].size();assert(len <= k);s[i] = " " + s[i];for (int j = 1; j < t[i - 1].size(); j++) w[j] = t[i - 1][j] - 'a' + 1;w[t[i - 1].size()] = 27;for (int j = 1; j <= len; j++) w[t[i - 1].size() + j] = s[i][j] - 'a' + 1;SA::build(w, len + t[i - 1].size());top = 0;auto chk = [&](pair <int, int> a, pair <int, int> b) -> int {int rev = 1, res = 0;if (a.first > b.first) swap(a, b), rev = -1;if (a.first == b.first) return 0;if (!a.second) return 0;int pa = t[i - 1].size() + 1, pb = a.first + 1;int lcp = SA::query(pa, pb), d = min(len, b.first - a.first);if (lcp < d) {res = w[pa + lcp] < w[pb + lcp] ? -1 : 1;return res * rev;}if (a.first + len <= b.first) return 0;if (!b.second) return 0;pa += d, pb = t[i - 1].size() + 1;lcp = SA::query(pa, pb);if (lcp < len - d) {res = w[pa + lcp] < w[pb + lcp] ? -1 : 1;return res * rev; }return 0;};for (int j = 0; j <= k; j++) {if (!suf[i + 1][k - j]) continue;pair <int, int> now = {-1, -1};if (f[i - 1][j]) now = {j, 0};if (j >= len && f[i - 1][j - len]) { if (now.first == -1) now = {j - len, len};else if (chk(now, make_pair(j - len, len)) == 1) now = {j - len, len};}if (now.first == -1) continue;while (top && chk(stk[top], now) == 1) f[i][stk[top].first + stk[top].second] = 0, top--;if (!top || !chk(stk[top], now)) f[i][j] = 1, stk[++top] = now;}t[i] = " ";for (int j = 1; j <= stk[top].first; j++) t[i] += t[i - 1][j];for (int j = 1; j <= stk[top].second; j++) t[i] += s[i][j];}for (int i = 1; i < t[n].size(); i++) cout << t[n][i];QwQ01AwA;
}