魔法开锁
小明有 \(n\) 个盒子,每个盒子被一把锁锁着,每个盒子内都有一把钥匙。对于每个盒子而言有且仅有一把钥匙能打开锁着它的锁,而打开它后便能拿着放置在这个盒子内的钥匙去开启其他盒子。
现在小明打算随机选择 \(t\) 个盒子并用魔法将它们打开,并用所得到的钥匙去尝试开启其他所有的盒子(开启一个盒子后,新得到的钥匙还能继续尝试使用)。
小明想知道,最终他能打开所有盒子的概率是多少,请你帮助他。
概率: 答案方案数 / 总方案数
总方案数就是 \(c(n,t)\) ,
那么如何才合法?
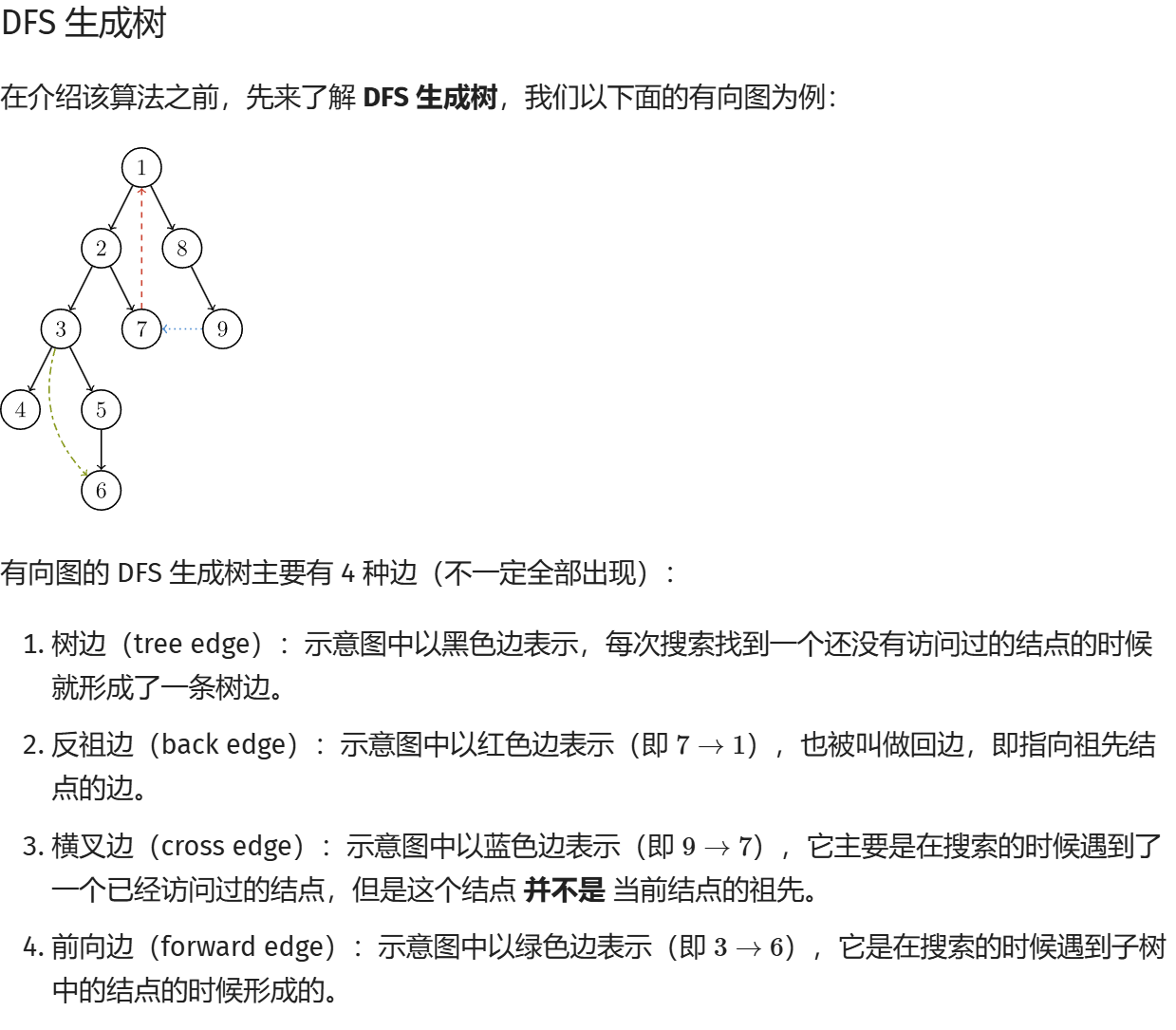
把盒子和盒子里的钥匙能开的盒子连边,会连成好几个环
选的 \(t\) 个点只要覆盖了所有环就合法
设 \(f_{i,j}\) 表示考虑前 \(i\) 个环,选了 j 个点的方案数
记环的大小为 \(num_{i}\)
转移为 \(f_{i,j}=\sum_{k=0}^{j-1} f(i-1,k) *c(num_i,j-k)\)
石子合并
在一个圆形操场的四周摆放 \(N\) 堆石子,现要将石子有次序地合并成一堆。规定每次只能选相邻的 \(2\) 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 \(N\) 堆石子合并成 \(1\) 堆的最小得分和最大得分。
破环成链
设合并 \(l,r\) 的最小得分 , 枚举断点 \(k\)
\(f_{l,r} = min(f_{l,k-1}+f_{k,r})+\sum_{i=l}^r a_i\)
木板涂色
可以一次给一个区间涂色
请你用尽量少的涂色次数达到目标。
当 \(s[l]!=s[r]\) \(f_{l,r}=f_{l,k}+f_{k+1,r}\)
当 \(s[l]!=s[r]\) \(f_{l,r}=min(f_{l,r-1},f_{l+1,r})\)
消除木块
\(n\) 个木块排成一列,每个木块都有一个颜色。
例如下图中木块的颜色分别为:金,银,银,银,银,铜,铜,铜,金。
每次,你都可以点击一个木块,这样被点击的木块以及和它相邻并且同色的木块就会消除。 如果一次性消除了 \(k\) 个木块,那么就会得到 \(k*k\) 分。 例如下图所示,点击银色木块,四个木块被消去,得到 \(16\) 分。
给定你一个游戏初始状态,请你求出最高得分是多少
设 \(f_{i,j,k}\) 表示 \(i,j\) 区间后面后接上了 \(k\) 个与 \(r\) 颜色相同的点 消除 \(i,j\) 这个区间的得分
直接消除:\(f_{i,j,k}=f_{i,j-1,0}+(len+k)^2\)
在 \(i,j\) 中找一个点 \(m\) m 的颜色与 r 相同:
\(f_{i,j,k}=max(f_{i,m,k+len_{r}}+f_{m+1,j-1,0})\)
哦,不知道转移顺序怎么办?
记搜
#include <bits/stdc++.h>
using namespace std;
int t,n,a[205],col[205],c[205],len[205],f[205][205][205];
int solve(int l,int r,int k){if(f[l][r][k])return f[l][r][k];if(l==r)return (len[r]+k)*(len[r]+k);f[l][r][k]=solve(l,r-1,0)+(len[r]+k)*(len[r]+k);for(int i=l;i<r;i++){if(c[i]==c[r]){f[l][r][k]=max(f[l][r][k],solve(i+1,r-1,0)+solve(l,i,len[r]+k));}}return f[l][r][k];
}
int main(){cin>>t;for(int i=1;i<=t;i++){cin>>n;cin>>col[1];int len1=1,tot=0;for(int i=2;i<=n;i++){cin>>col[i];if(col[i]!=col[i-1]){tot++;c[tot]=col[i-1];len[tot]=len1;len1=1;}else len1++;}if(len1){c[++tot]=col[n];len[tot]=len1;}for(int j=1;j<=tot;j++){for(int k=1;k<=n;k++){f[j][j][k]=(len[j]+k)*(len[j]+k);}}cout<<"Case "<<i<<": "<<solve(1,tot,0)<<endl;memset(f,0,sizeof(f));}return 0;
}