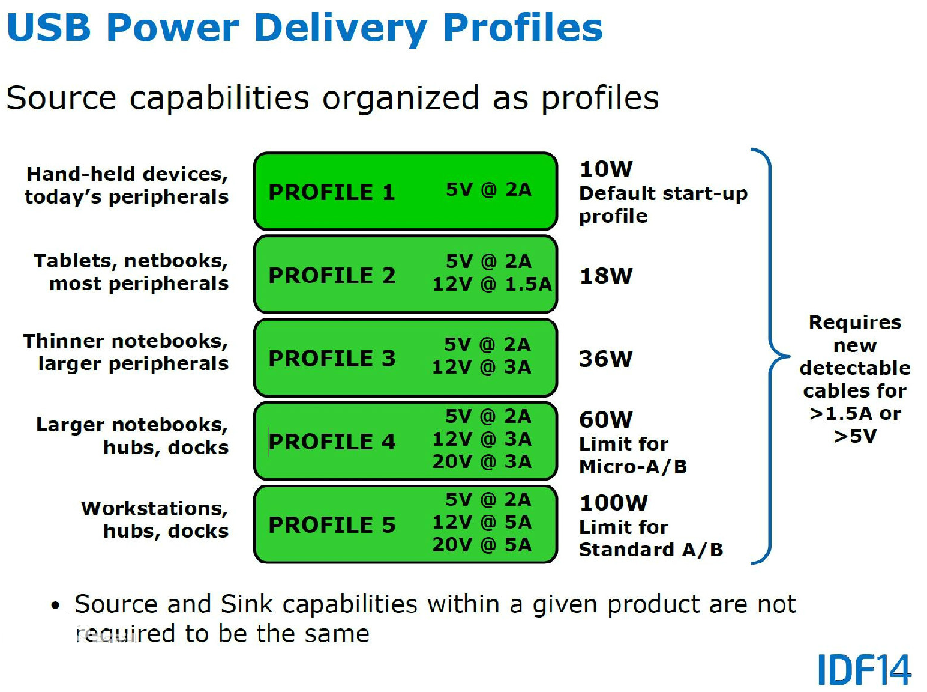
运输计划
显然我们可以处理出每个区间正方向和反方向走的代价,那么最后的问题可以转化为每个点选择 \(0/1\) 之一,要求区间的选择两两不冲突,在这个基础上最小化代价之和。
则,可以参考 \(2-SAT\) 的思路,处理出每个点选择 \(0/1\) 两两的限制状况,不难发现这种限制应该是对称的,而且有一些限制是双向的。
为了方便讨论,我们钦定所有区间为顺时针顺序从 \(s\) 指向 \(t\) 。
参考物理学上理想化模型的方法,考虑最简化的情况,即只有两个区间的时候。
显然,两个区间的状态只有 “相交”,“相离”,“包含”,三种关系。
对于 “相交” 我们发现, 这两个区间的 \(0/1\) 状况必然是一样的。
而 “相离” 也是同理。
最后的包含特殊一些,若 \(a\rightarrow b\),则 \(a\) 取 \(1\) 那么 \(b\) 必须取值 \(1\),\(b\) 取 \(0\) 那么 \(a\) 必须取 \(0\)。
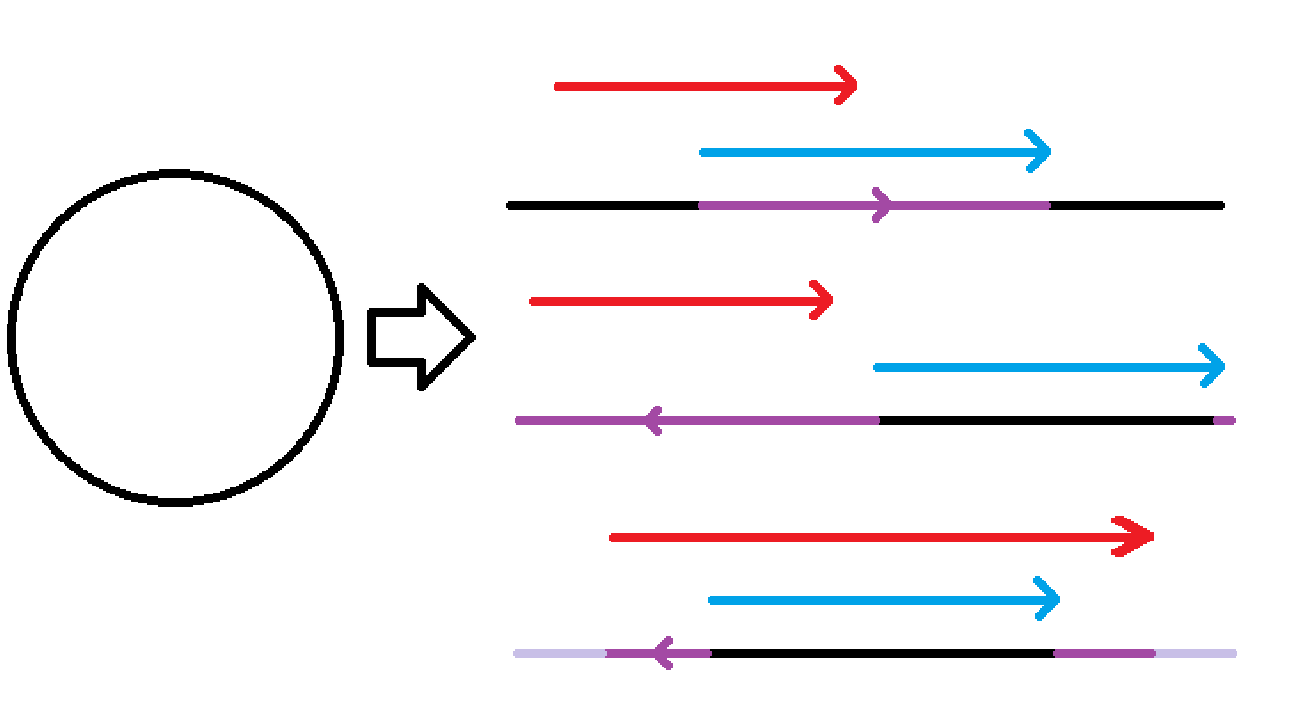
由此,我们可以 \(O(n^2)\) 判定两个区间的关系,并连边建出一张图,然后 Tarjan 缩点(不难发现缩点之后的形态一定是一条链),在链上枚举一下 \(0,1\) 交界计算贡献。
考虑优化整个建图过程,我们发现建图本身是一个查询二维偏序的点的过程,所以直接狂暴线段树优化建图即可。
但是太狂暴了。
所以考虑另一种优化思路,我们发现,如果有若干个区间两两相离,它们会形成一个完全图,而最后都会缩成一个点。
那么就没有必要把这样的完全图建出来,只需要相邻的两个相离区间连边即可。
同样,对于相交的区间,只需要相邻的两个相交区间连双向边即可。
那么现在要处理的问题是包含关系。
不难发现,包含关系也只需要处理一级包含即可。
所以我们将所有区间按照右端点排序(右端点相同的按左端点排序),从左到右扫描每个区间,用一个栈维护当前相离的所有区间,每次新加入一个区间的时候将所有被这个区间包含的区间出栈,然后可能会出现一个于它相交的区间,也出栈,如果栈里还剩有区间,那么一定是左边某个和它相离的区间。
对于每一类区间按照上述规则连边即可。
但是还有个问题,比如遇到形如
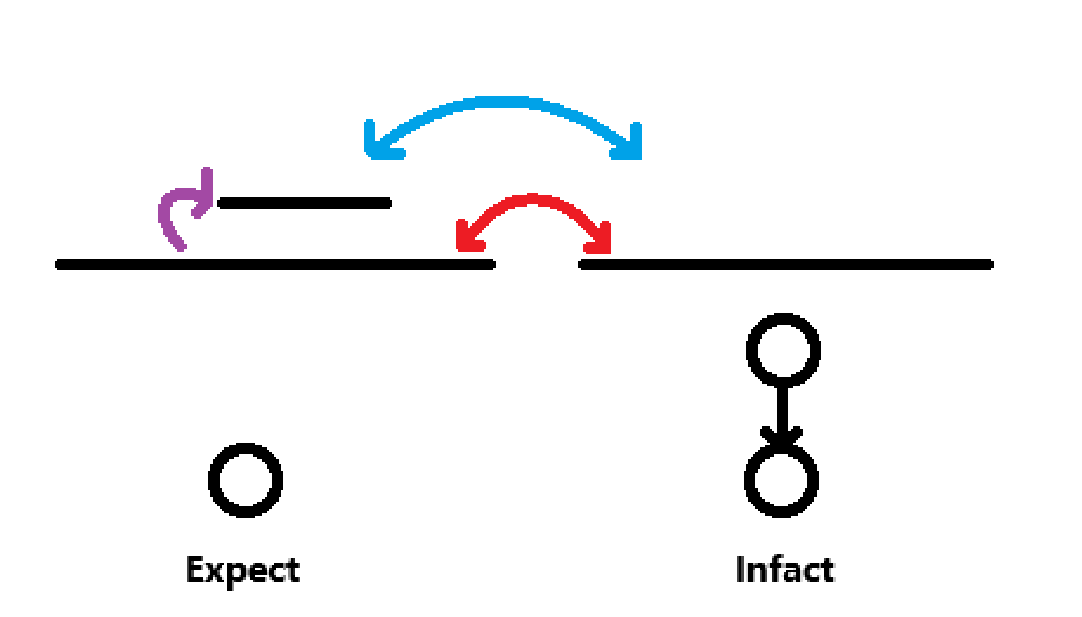
本来应该两个点都和右边的区间连双向边的,但由于其中一个被覆盖了,导致另一个边无法访问其。
解决方法很简单,按右端点排序左端点升序降序各跑一遍,按左端点排序右端点升序降序各扫一遍,那么每一条链最下面那个点和最上面那个点都连上了双向边,就避免了这种情况的出现。
实际上做法还有很大一堆,这里推荐一种 @Rain 的优雅做法。
最初全顺时针定向,处理好全顺/逆的答案。对于一对区间,若相离,则必须不变向(不然就是全顺/逆了),若相交,则必须同时变/不变,若包含,则只有外层变了内层才能变。
按套路断环为链,讨论每一个区间是否有相离。求出若干固定区间后,把这些的相交区间也搞出来 (这里由于数据水,没写),它们都必须不变。
对于剩下的 “全包含固定的区间的” 区间,它们的开口必须在同一个空隙 (由于数据水,也没判),然后,重标号,使它们的交位于正中间,那么一个区间左端点必然在 \([1,n]\),右端点必然在 \([n+1,2n]\)。拍到二维平面上,求右上角的覆盖点。被覆盖的点一定和覆盖点等价。但是注意一个麻烦的地方,轮廓上的点可以被内部的点合并,所以在用并查集维护一个真正的可选变不变的点集。因为每次都是区间 merge,所以并查集加速即可。(由于数据太水,最开始逆时针重标号可以直接过,所以就没写)
时间复杂度 \(O(n\log_2n)\) 实际上可以用基数排序做到 \(O(n)\)。