本文将深入探讨概率分布,详细阐述概率质量函数(PMF)、概率密度函数(PDF)和累积分布函数(CDF)这些核心概念,并通过实际示例进行说明。
在深入探讨PMF、PDF和CDF之前,有必要先简要介绍两种常用的概率分布:正态分布和均匀分布。
正态分布: 也称为高斯分布或钟形曲线,正态分布以其均值为中心对称。它广泛应用于描述自然界中的许多现象。诸如人口身高、标准化考试成绩、测量误差等多种实际数据集都呈现正态分布特征。
均匀分布: 在均匀分布中,给定范围内的每个结果具有相等的概率。这是最基本的概率分布形式,常用于描述每个结果等可能出现的情况,如公平骰子的投掷结果或0到1之间随机数的选取。
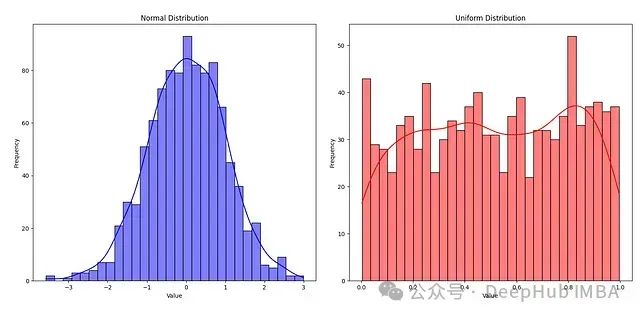
图1左侧展示了正态分布,呈现典型的钟形曲线,以平均值(此处为0)为中心。可以观察到,大多数数值集中在中心区域。右侧图表表示均匀分布,在0到1之间呈现均匀分布,表明每个值具有相等的出现概率。
在数据科学和统计学研究中,理解概率分布方式是核心任务。概率分布函数在这方面发挥着关键作用。本文将详细讨论概率密度函数(PDF)、概率质量函数(PMF)和累积分布函数(CDF)的概念。我们还将探讨如何从PMF或PDF推导CDF,并为每种情况提供具体示例。
https://avoid.overfit.cn/post/4571cfdbae7b43b2b6db94769f433d66