- 一、微分的定义
- 二、微分的几何意义
- 三、微分运算
- 1、函数和、差、积、商的微分法则
- 2、复合函数的微分法则
- 四、微分在近似计算中的应用
一、微分的定义
定义 设函数 \(y = f(x)\) 在某区间内有定义,\(x_0\) 及 \(x_0 + \Delta x\) 在这区间内,如果函数的增量
\[\Delta y = f(x_0 + \Delta x) - f(x_0) \]可表示为
\[\Delta y = A \Delta x + o(x) , \tag{1} \]其中 \(A\) 是不依赖于 \(\Delta x\) 的常数,那么称函数 \(y = f(x)\) 在点 \(x_0\) 是可微的,而 \(A \Delta x\) 叫做函数 \(y = f(x)\) 在点 \(x_0\) 相应于自变量增量 \(\Delta x\) 的微分,记作 \(\mathrm{d}y\) ,即
\[\mathrm{d}y = A \Delta x \]
下面讨论函数可微的条件。设函数 \(y = f(x)\) 在点 \(x_0\) 可微,则按定义有 \((1)\) 式成立。\((1)\) 式两边除以 \(\Delta x\) ,得
于是,当 \(\Delta x \to 0\) 时,由上式可得
因此,如果函数 \(y = f(x)\) 在点 \(x_0\) 可微,那么 \(f(x)\) 在点 \(x_0\) 也一定可导(即 \(f'(x_0)\) 存在),且 \(A = f'(x_0)\) 。
反之,如果 \(y = f(x)\) 在点 \(x_0\) 可导,即
存在,根据极限与无穷小的关系,上式可写成
其中 \(\alpha \to 0\) (当 \(\Delta x \to 0\))。由此又有
因 \(\alpha \Delta x = o(x)\) ,且 \(f'(x)\) 不依赖于 \(\Delta x\) ,故上式相当于 \((1)\) 式。所以 \(f(x)\) 在点 \(x_0\) 也是可微的。
由此可见,函数 \(f(x)\) 在点 \(x_0\) 可微的充分必要条件是函数 \(f(x)\) 在点 \(x_0\) 可导,且当 \(f(x)\) 在点 \(x_0\) 可微时,其微分一定是
当 \(f'(x) \neq 0\) 时,有
从而,当 \(\Delta \to 0\) 时,\(\Delta y\) 与 \(\mathrm{d}y\) 是等价无穷小,于是有
即 \(\mathrm{d}y\) 是 \(\Delta y\) 的主部。又由于 \(\mathrm{d}y = f'(x) \Delta x\) 是 \(\Delta x\) 的线性函数,所以在 \(f'(x_0) \neq 0\) 的条件下,我们说 \(\mathrm{d}y\) 是 \(\Delta y\) 的线性主部(当 \(\Delta x \to 0\)).于是我们得到结论:在 \(f'(x_0) \neq 0\) 的条件下,以微分 \(\mathrm{d}y = f'(x_0) \Delta x\) 近似代替增量 \(\Delta y = f(x_0 + \Delta x) - f(x_0)\) 时,其误差为 \(o(\mathrm{d}y)\) ,因此,在 \(| \Delta x |\) 很小时,有近似等式
例1 求函数 \(y = x^2\) 在 \(x = 1\) 和 \(x = 3\) 处的微分。
解:函数 \(y = x^2\) 在 \(x = 1\) 处的微分为
在 \(x = 3\) 处的微分为
函数 \(y = f(x)\) 在任意点 \(x\) 的微分,称为函数的微分,记作 \(\mathrm{d}y\) 或 \(\mathrm{d} f(x)\) ,即
显然,函数的微分 \(\mathrm{d}y = f'(x) \Delta x\) 与 \(x\) 和 \(\Delta x\) 有关。
例2 求函数 \(y = x^3\) 当 \(x = 2\) ,\(\Delta x = 0.02\) 时的微分。
解:先求函数在任意点 \(x\) 的微分
再求函数当 \(x = 2\) ,\(\Delta x = 0.02\) 时的微分
通常把自变量 \(x\) 的增量 \(\Delta x\) 称为自变量的微分,记作 \(\mathrm{d}x\) ,即 \(\mathrm{d}x = \Delta x\) 。于是函数 \(y = f(x)\) 的微分又可以记作
从而有
这就是说,函数的微分 \(\mathrm{d}y\) 与自变量的微分 \(\mathrm{d}x\) 之商等于该函数的导数。因此,导数也叫做“微商”。
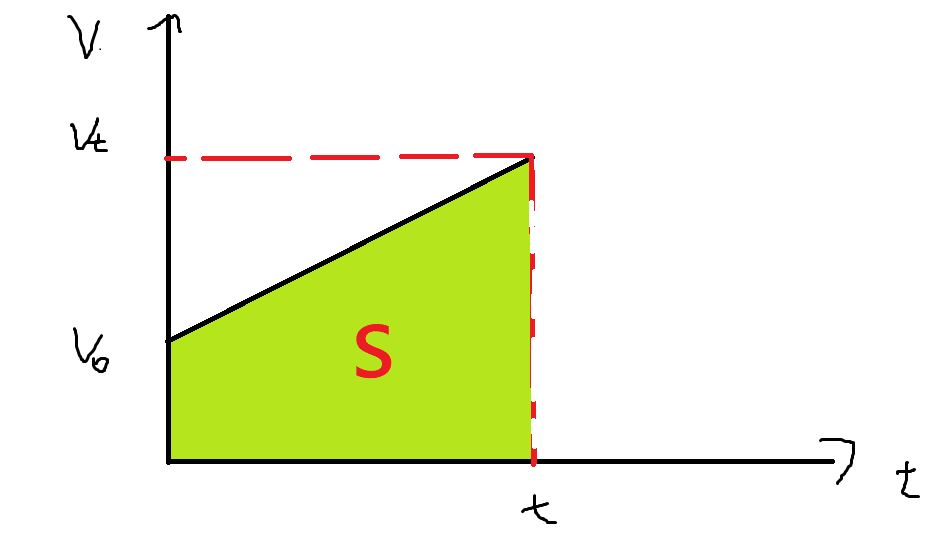
二、微分的几何意义

三、微分运算
从函数的微分的表达式
可以看出,要计算函数的微分,只需要计算函数的导数,再乘以自变量的微分。
1、函数和、差、积、商的微分法则
(1)\(\mathrm{d}(u \pm v) = \mathrm{d}u \pm \mathrm{d}v\) .
(2)\(\mathrm{d}(Cu) = C \mathrm{d}u\)
(3)\(\mathrm{d} (uv) = v \mathrm{d}u + u \mathrm{d}v\)
(4)\(\mathrm{d} \left( \cfrac{u}{v} \right) = \cfrac{v \mathrm{d}u - u \mathrm{d}v}{v^2} \quad (v \neq 0)\).
2、复合函数的微分法则
与复合函数的求导法则相应地复合函数的微分法则可推导如下:
设 \(y = f(u)\) 及 \(u = \mathrm{g}(x)\) 都可导,则复合函数 \(y = f[\mathrm{g}(x)]\) 的微分为
由于 \(\mathrm{g}'(x) \mathrm{d}x = \mathrm{d}u\) ,所以,复合函数 \(y = f[\mathrm{g}(x)]\) 的微分公式也可以写成
由此可见,无论 \(u\) 是自变量还是中间变量,微分形式 \(\mathrm{d}y = f'(u) \mathrm{d}u\) 保持不变。这一性质称为微分形式不变性。这性质表示,当变换自变量时,微分形式 \(\mathrm{d}y = f'(u) \mathrm{d}u\) 并不改变。
例3 设 \(y = \sin{(2x + 1)}\) ,求 \(\mathrm{d}y\) .
解:把 \(2x + 1\) 看成中间变量 \(u\) ,则
例4 设 \(y = \ln{(1 + \mathrm{e}^{x^2})}\) ,求 \(\mathrm{d}y\)
解:
例5 设 \(y = \mathrm{e}^{1 - 3x} \cos x\) ,求 \(\mathrm{d}y\) 。
解:应用积的微分法则,得
四、微分在近似计算中的应用
在工程问题中,经常会遇到一些复杂的计算公式。如果直接用这些公式进行计算,那是很费力的。利用微分往往可以把一些复杂的计算公式用简单的近似公式来代替。
前面说过,如果 \(y = f(x)\) 在点 \(x_0\) 处的导数 \(f'(x_0) \neq 0\) ,且 \(| \Delta x |\) 很小时,我们有
这个式子也可以写为
或
在 \((5)\) 式中令 \(x = x_0 + \Delta x\) ,即 \(\Delta x = x - x_0\) ,那么 \((5)\) 式可以写为
如果 \(f(x_0)\) 与 \(f'(x_0)\) 都容易计算,那么可以利用 \((4)\) 式来近似计算 \(\Delta y\) ,利用 \((5)\) 式来近似计算 \(f(x_0 + \Delta x)\) ,或利用 \((6)\) 式来近似计算 \(f(x)\) 。这种近似计算的实质就是用 \(x\) 的线性函数 \(f(x_0) + f'(x_0) (x - x_0)\) 来近似表达函数 \(f(x)\) 。从导数的几何意义可知,这也就是用曲线 \(y = f(x)\) 在点 \((x_0, f(x_0))\) 处的切线来近似代替该曲线(就切点邻近部分来说)。
例7 有一批半径为 \(1 \mathrm{cm}\) 的球,为了提高球面的光洁度,要镀上一层铜,厚度定为 \(0.01 \mathrm{cm}\) 。估计一下镀每只球需用多少克铜(铜的密度是 \(8.9 \mathrm{g}/\mathrm{cm}^3\))。
解:先求出镀层的体积,再乘密度就可得到镀每只球需用的铜的质量。
因为镀层的体积等于镀铜前、后两个球体体积之差,所以它就是球体体积 \(V = \cfrac{4}{3} \pi R^3\) 当 \(R\) 自 \(R_0\) 取得增量 \(\Delta R\) 时的增量 \(\Delta V\) 。我们求 \(V\) 对 \(R\) 的导数。
可得
将 \(R_0 = 1\) , \(\Delta R = 0.01\) 代入上式,得
于是镀每只球需用的铜约为
例8 利用微分计算 \(\sin{30^{\circ} 30 ^\prime}\) 的近似值。
解:把 \(\sin{30^{\circ} 30^\prime}\) 化为弧度,得
由于所求的是正弦函数的值,故设 \(f(x) = \sin x\) 。此时 \(f^{'} = \cos x\) 。如果取 \(x_0 = \cfrac{\pi}{6}\) ,那么 \(f \left( \cfrac{\pi}{6} \right) = \sin{\cfrac{\pi}{6}} = \cfrac{1}{2}\) 与 \(f^{'} \left( \cfrac{\pi}{6} \right) = \cos{\cfrac{\pi}{6}} = \cfrac{\sqrt 3}{2}\) 都容易计算,并且 \(\Delta x = \cfrac{\pi}{360}\) 比较小,可得
在 \((6)\) 式中取 \(x_0 = 0\) ,于是得
应用 \((7)\) 式可以推得以下几个在工程上常用的近似公式(下面都假定 \(|x|\) 是比较小的数值):
(1)\((1 + x)^{\alpha} \approx 1 + \alpha x \quad (\alpha \in \mathbb{R})\)
(2)\(\sin x \approx x (x以弧度为单位)\)
(3)\(\tan x \approx x (x以弧度为单位)\)
(4)\(\mathrm{e}^x \approx 1 + x\)
(5)\(\ln{(1 + x)} \approx x .\)
例9 计算 \(\sqrt{1.05}\) 的近似值。
解:
这里 \(x = 0.05\) ,其值较小,利用近似公式(1)可得