图论指标在认知神经科学或脑科学的研究中,通常作为研究脑网络表现的描述性指标之一,而图论指标从全局性来分可以分为:节点指标和全局指标,而根据描述脑网络整合性表现又可分为:整合指标和分离指标。
该随笔主要涉及图论指标中全局指标及整合指标的全局集群系数,英文全称为Global Clustering coefficient。
在学习该指标前,我们需要先了解一个核心概念——三角形。听起来,这个概念似乎很简单。是的!这个概念并不复杂,甚至可以说非常简单。现在,我们可以在纸上画出一个三角形,这个三角形有边,而边与边相交处便是交点。在认知神经科学研究中,无论是fMRI、fNIRS或者是EEG,我们在收集脑信号都是基于点的,如fMRI的体素,fNIRS和EEG的通道。这些点边可以看成是三角形的交点,而但点与点之间存在相关时便可以连成边,而三个这样的边便可以形成三角形。
在整个脑网络中,能够形成三角形数量的多少决定了整个网络倾向于形成紧密连接群体的程度,也即整合程度。
那么问题就来了,为什么我们会选择三角形作为最基本的元素?
“三人成虎”,一个中国成语可能能很好地解释这个问题。相比于两个节点形成的边,三个节点形成的三角能够提供更为丰富的信息,它体现了群体效应。三角形形成了完整的闭环关系,这种结构表征了节点间更为复杂的交互模式,它是一种社区结构。最后,在实际中,三角形在信息传递和冗余性上有着一定的优势,例如三角形中即使某一个边出现问题,信息仍然可以有效传递。
回归正题!那么全局集群系数是怎么计算的?
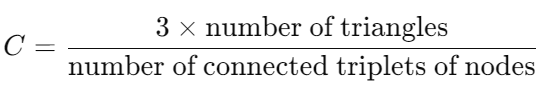
全局聚类系数通常定义为网络中实际存在的三角形数量与能够形成三角形的三元组(由三个节点构成,其中至少有两条边将它们连接起来)数量的比值。
相应的,既然具有全局集群系数,那就存在局部集群系数,该指标的意义请关注后续更新内容。
![day4[大模型全链路开源开放体系学习小结]](https://img2024.cnblogs.com/blog/3229976/202409/3229976-20240919221557938-274890735.png)