单项选择
1
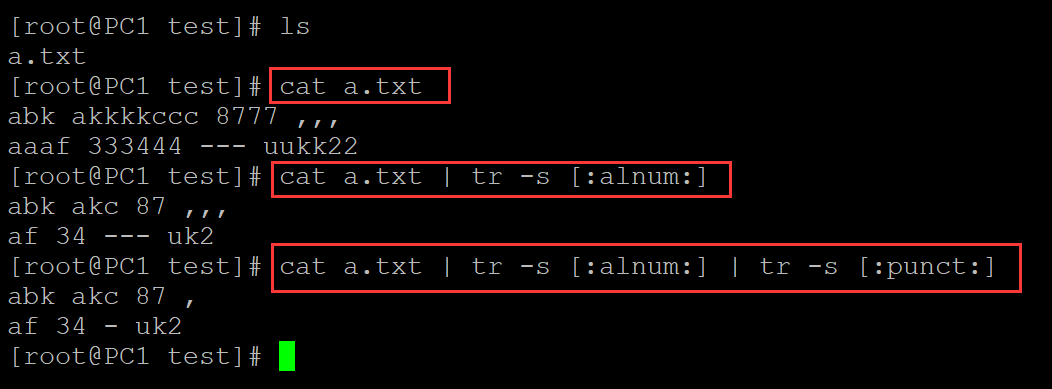
在 Linux 系统中,如果你想显示当前工作目录的路径,应该使用哪个命令?
A
pwd
Bcd
Cls
Decho
pwd : print working directory
cd : 跳转到指定目录
ls : 列出当前目录的所有子文件和子文件夹
echo : 输出指定内容
2
假设一个长度为n的整数数组中每个元索值互不相同,且这个数组是无序的。要找到这个数组中最大元素的时间复杂度是多少?
A \(O(n)\)
B \(O(logn)\)
C \(O(nlogn)\)
D \(O(1)\)
无序的数组只能通过两两比较来查找,需要比较 \(n-1\) 次(第一次不需要比较),因此为 \(O(n)\)
3
在 C++中,以下哪个函数调用会造成溢出?
A
int foo(){ return 0;}
Bint bar(){int x=1;return x; }
Cvoid baz(){ int a[1000];baz();)
Dvoid qux(){ return; }
函数栈溢出一般有两种:函数内变量开的太大,或者函数递归深度太深
这里 baz() 函数重复调用自身,无终止条件,因此会溢出
4
在一场比赛中,有 \(10\) 名选手参加,前三名将获得金、银、牌。若不允许并列,且每名选手只能获得一枚奖牌,则不同的颁奖方式有多少种?
A 120
B 720
C 504
D 1000
不妨选出一个长度为 \(3\) 的序列,依次获得金,银,铜牌,则方案有 \(A^{3}_{10}=10\times 9\times 8=720\) 种
5
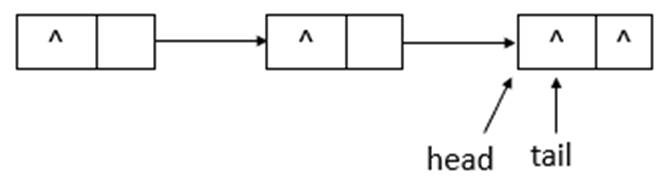
下面哪个数据结构最适合实现先进先出(FIFO)的功能?
A 栈
B 队列
C 线性表
D 二叉搜索树
栈是先进后出
后面两种数据结构不具备存放与弹出基本数据的功能
线性表在功能上类似数组
6
已知 \(f(1)=1\),且对于 \(n\ge2\) 有 \(f(n)=f(n-1)+f(⌊n/2⌋)\) ,则 \(f(4)\) 的值为:
A \(4\)
B \(5\)
C \(6\)
D \(7\)
\(f(2)=f(1)+f(1)=2\)
\(f(3)=f(2)+f(1)=3\)
\(f(4)=f(3)+f(2)=5\)
7
假设有一个包含 \(n\) 个顶点的无向图,且该图是欧拉图。以下关于该图的描述中哪一项不一定正确?
A 所有顶点的度数均为偶数
B 该图连通
C 该图存在一个欧拉回路
D 该图的边数是奇数
欧拉图定义:仅由欧拉回路构成的图
欧拉回路:即一笔能画完的图。形式化地说,欧拉回路是从任意一个点出发,不重复经过任何一条边,也不遗漏任何一条边,最终仍能回到该节点的路径
根据定义,D 是错误的,反例为一个正方形
8
对数组进行二分查找的过程中,以下哪个条件必须满足?
A 数组必须是有序的
B 数组必须是无序的
C 数组长度必须是 \(2\) 的幂
D 数组中的元素必须为整数
二分查找本质上也是一种二分答案,需要保证答案具有单调性
9
考虑一个自然数 \(n\) 以及一个数 \(m\),你需要计算 \(n\) 的逆元(即 \(n\) 在 \(m\) 意义下的乘法逆元),下列哪种算法最为适合?
A 使用暴力法依次尝试
B 使用扩展欧几里得算法
C 使用快速幂法
D 使用线性筛法
逆元的定义是这样的:
定义 \(a\) 在模 \(p\) 意义下的逆元 \(b\) 满足 \((\frac{c}{a})\mod p=(c\times b)\mod p\)
当 \(p\) 为质数的时候,才能使用快速幂(+费马小定理)来求逆元,而扩展欧几里得算法为更加通用的求逆元方法,只需要满足两个数互质
更详细的求逆元方法可以通过 这篇文章 的 5.3.1 章了解
10
在设计一个哈希表时,为了减少冲突,需要使用适当的哈希函效和冲突解决策略。已知某哈希表中有 \(n\) 个键值对,表的装载因子为 \(a(0<a\le 1)\) 。在使用开放地址法解决冲突的过程中,最坏情况下查找一个元素的时间复杂度为
A \(O(1)\)
B \(O(logn)\)
C \(O(1/(1-a))\)
D \(O(n)\)
开放地址法解决冲突:假设当前元素 \(x\) 需要放入地址 \(p\) 中,但现在 \(p\) 位置已经有了元素,直接放置就会导致冲突,因此考虑向后依次找,找到第一个没有放置元素的位置放置,这样可以防止冲突(遍历到最后再从头开始)
因此最坏情况下需要把整个表遍历一遍,复杂度为 \(O(n)\)
科普装载因子的定义:装载因子定义了一个阈值,当哈希表中的条目数超出了加载因子与当前容量的乘积时,则要对该哈希表进行扩容、rehash操作(即重建内部数据结构),扩容后的哈希表将具有两倍的原容量。
11
假设有一棵 \(h\) 层的完全二叉树,该树最多包含多少个结点?
A \(2^h-1\)
B \(2^{h+1}-1\)
C \(2^h\)
D \(2^{h+1}\)
因为每个节点都有两个儿子,因此每一层的节点个数都是上一层的两倍
总结点数为 \(1+2^{1}+2^{2}+\cdots+2^{h-1}=2^{h}-1\)
12
设有一个 \(10\) 个顶点的完全图,每两个顶点之间都有一条边。有多少个长度为 \(4\) 的环?
A \(120\)
B \(210\)
C \(630\)
D \(5040\)
因为图完全联通,任取四个点一定能保证它们构成一个环
因为环上的点是无序的,因此很多人会考虑计算 \(C^{4}_{10}=\frac{10\times 9\times 8\times 7}{4\times 3\times 2\times 1}=210\),然而这样是错误的
考虑是什么地方出了问题
刚才我们说,任取四个点一定能保证它们构成一个环
但是环 1 2 3 4 和环 2 1 3 4 并不是同一个环,前者有 1->2->3 的连边,后者有 2->1->3 的连边,显然不是同一个环
正确的做法是考虑重复的环:
注意到 1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3 是重复的,以此类推,每一种可能的组合都有四种可能的起始节点,因此会重复计算 \(4\) 次
另外,注意到 1 2 3 4 4 3 2 1 是重复的,同样,上面的每一种反过来和原来都是一样的,因此答案为 \(\frac{A^{4}_{10}}{2\times 4}=630\)
13
对于一个整数 \(n\)。定义 \(f(n)\) 为 \(n\) 的各位数字之和。问使 \(f(f(x))=10\) 的最小自然数 \(x\) 是多少?
A \(29\)
B \(199\)
C \(299\)
D \(399\)
代选项即可
\(f(29)=11,f(f(29))=2\)
\(f(199)=19,f(f(199))=10\)
\(f(299)=20,f(f(299))=2\)
\(f(399)=21,f(f(399))=3\)
14
设有一个长度为 \(n\) 的 01 字符串,其中有 \(k\) 个 \(1\) ,每次操作可以交换相邻两个字符。在最坏情况下将这 \(k\) 个 \(1\) 移到字符串最右边所要的交换次数是多少?
A \(k\)
B \(\frac{k\times (k-1)}{2}\)
C \((n-k)\times k\)
D \(\frac{(2n-k-1)\times k}{2}\)
D 这个数的来源:令全部数字都排在最左边,然后从右到左一个一个挪,然后认为答案是 \((n-1)+(n-2)+(n-3)\cdots+(n-k)\)
实际上,在排后面的数字时,由于右边已经有排好的数字,不需要将新来的数字与排好的数字进行比较与交换了,所以每个数字的交换次数只有 \((n-k)\) 次,一共 \(k(n-k)\) 次
15
如图是一张包含 \(7\) 个顶点的有向图,如果要除其中一些边,使得从节点 \(1\) 到节点 \(7\) 没有可行路径,且删除的边数最少,请问总共有多少种可行的删除边的集合?
A \(1\)
B \(2\)
C \(3\)
D \(4\)

一个可能更丑的图

上来先注意到 \(\{8,9\}\) 是合法的,并且不存在只删一个边的解法,因此最优解为 \(2\)
可行的边的集合
\(\{8,9\}\)
\(\{5,6\}\)
\(\{6,8\}\)
\(\{1,6\}\)
![[CVPR2024]DeiT-LT Distillation Strikes Back for Vision Transformer Training on Long-Tailed Datasets](https://img2023.cnblogs.com/blog/3039442/202409/3039442-20240922204641858-1290751669.png)