用来整理模拟赛等
9.23
csp-3【noip23 ZR二十连测 DAY10】
保龄.
A.奇观
狗市题目描述。

不是这题意太大歧义了吧,我讨厌的第二种出题人——题意描述相当不清。
CTH:13 座城市又不代表是 13 座不同的城市。
直接看形式化题目的话(如果能看懂要干什么)那这题确实不难。
解:
容易发现,答案就是 \(C\times C \times F\)。(\(C、F\) 分别表示组成一个 C、F 的方案数)
关键在于 \(CCF\) 怎么求?看懂题意的话,较容易明白:
记 \(v1_i =∑_j[(i, j) ∈ E] ,v2_i=∑_{j,k} [(i, j) ∈ E ∧ (j, k) ∈ E] = ∑_j[(i, j) ∈ E]v1_j\);
分别为以 \(i\) 为端点能拼成如下形式的方案数。
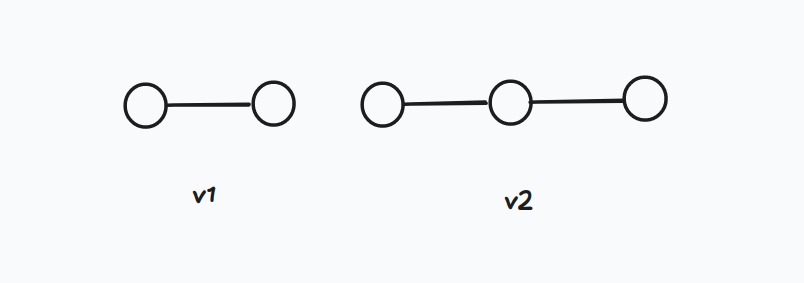
那么有 \(C=\sum_i v1_i\times v2_i\) , \(F = \sum v1_i \times \ v1_i \times v2_i\) 。
显然 \(v1_i\) 其实就等于删去 \(m\) 条边后的出度。现在考虑 \(v2_i\) 如何求。
我们再求一个 \(sum=\sum_i v1_i\),把每个 \(v2_i\) 都赋成 \(sum\),删去了哪些 \(i,j\) 相连的边,就减去 \(v1_j\) 即可。
B.铁路

随便钦定一个根跑 \(dfs\) 得到所有点的深度 \(dep\) 和父节点 \(fa\)
并查集维护连通块,每次把要合并的点都合并到其中深度最浅的点的并查集上,把 \(n+i\) 映射到这个最浅点上就好了。
C.光纤
9.24 补 从下午 14:00 调到 21:00,救命啊!
需要知识:凸包 向量叉积 旋转卡壳
- 构建一个包含所有点的凸包。
丁真的引理:答案直线就是平行于凸包所有边的直线中最优的那个。
显然:对于凸包的一条边,凸包上的点到该边的距离中最大的那个的一半就是该边对答案的贡献。
如下图中蓝边对于答案的贡献就是红色虚线(最远点到该边距离)的一半。
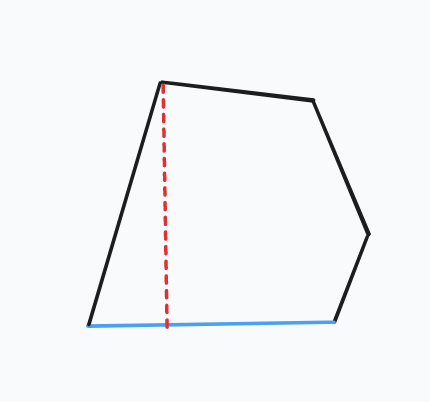
- 旋转卡壳 \(O(n)\) 找凸包上的每一条边的最远点,叉积计算最远点的距离,计算答案。
code
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;const int N = 1e6 + 10;int n, m, top, H;
pair<__int128, __int128>ans;struct point{__int128 x, y;bool operator < (const point &A)const{return x == A.x ? y < A.y : x < A.x;}
}a[N], s[N], q[N];char anss[N];
inline void print(__int128 x){if(!x)putchar('0');else{if(x<0)x=-x,putchar('-');int cnt=0;while(x)anss[++cnt]=x%10+'0',x/=10;for(int i=cnt;i;--i)putchar(anss[i]);}
}point operator - (point A, point B){return {A.x - B.x, A.y - B.y};}inline double Cross(point A, point B){return (double)(B.y - A.y) / (B.x - A.x);} //算直线斜率inline void Andrew(){ //Andrew 算法建凸包for(int i=1; i<=n; i++){while(top > 1 and Cross(s[top], a[i]) <= Cross(s[top-1], s[top])) top--;s[++top] = a[i];}int k = 0;for(int i=n; i>=1; i--){while(k > 1 and Cross(a[i], q[k]) <= Cross(q[k], q[k-1])) k--;q[++k] = a[i];}for(int i=2; i<k; i++) s[++top] = q[i];s[++top] = s[1]; // s[] 中存凸包上的每个点
}inline __int128 Pf(__int128 x){return x * x;}inline __int128 dis(point a, point b){return Pf(a.x - b.x) + Pf(a.y - b.y);}inline __int128 _abs(__int128 x) {return x > 0 ? x : -1 * x;}inline __int128 GetSum(point a, point b, point c){ //已知 a,b,c 三点,叉积求三点围成的三角形面积的两倍return _abs((b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y));
}inline void GetHigh(){int j = 3; //旋转卡壳计算答案for(int i=1; i<top; i++){while(GetSum(s[i], s[i+1], s[j]) <= GetSum(s[i], s[i+1], s[j+1==top ? 1:j+1]))j = (j + 1 == top ? 1 : j + 1);if(!ans.second or 1.0 * ans.first / ans.second > 1.0 * Pf(GetSum(s[i], s[i+1], s[j])) / dis(s[i], s[i+1]))ans.first = Pf(GetSum(s[i], s[i+1], s[j])), ans.second = dis(s[i], s[i+1]); //first,second 分别为答案的分子分母}
}int main(){freopen("a.in", "r", stdin), freopen("a.out", "w", stdout);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin>>n;if(n == 2){cout<<"0/1\n"; return 0;}for(int i=1; i<=n; i++){int x, y; cin>>x>>y;a[i].x = x, a[i].y = y;}sort(a+1, a+1+n);n = unique(a+1, a+1+n, [](const point &A, const point &B){return A.x==B.x&&A.y == B.y;}) - (a+1);Andrew();GetHigh();__int128 gcd = __gcd(ans.first, ans.second*4); //因为面积算的是三角形的两倍,平方后就是四倍,分母乘以 4print(ans.first/gcd); putchar('/'); print(ans.second*4/gcd);return 0;
}