区间质数搜索——埃拉托斯特尼筛法和欧拉筛法

参考资料

【中国大学生计算机设计大赛国赛二等奖微课与教学辅助《埃拉托斯特尼筛法》】
【中国大学生计算机设计大赛《素数筛选—欧拉线性筛选法详解》】
Eratosthenes筛法-CSDN博客
【算法/数论】欧拉筛法详解：过程详述、正确性证明、复杂度证明-CSDN博客
水平有限，欢迎交流！

练习题

[编程入门]筛选 N 以内的素数 - C 语言网 (dotcpp. Com)

埃拉托斯特尼筛法算法

思想

步骤

埃拉托斯特尼筛法的基本步骤如下：

1. 创建一个列表：创建一个从2到n的数字列表。
2. 标记质数：从列表的第一个数（即2）开始，把它标记为质数。
3. 筛掉倍数：然后去掉列表中所有2的倍数（除了2本身），因为这些数都是合数。
4. 移动到下一个未标记的数：接下来，移动到列表中未被标记为合数的下一个数（此时是3），再次标记为质数，并筛掉它的所有倍数。
5. 重复步骤：重复上述过程，直到根号 n。

优化

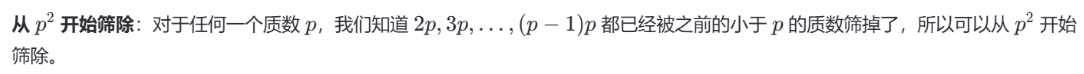
代码实现（以 java 为例）

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
    /** 优化埃氏筛法求质数
     * 获取小于等于n的所有质数
     * @param n 最大检查范围
     * @return 返回小于等于n的所有质数的列表
     */
    public static List<Integer> getPrimesBySieve(int n) {
        boolean[] st = new boolean[n + 1];
        List<Integer> primes = new ArrayList<>();
        for (int p = 2; p * p <= n; p++) {
            if (!st[p]) {  // 如果p还没有被标记，则它是质数
                primes.add(p);
                for (int i = p * p; i <= n; i += p) {
                    // 从p的平方开始，依次标记p的倍数
                    st[i] = true;  // 标记p的倍数为合数
                }
            }
        }
        // 添加剩余的大于sqrt(n)的质数
        for (int p = (int)Math.sqrt(n) + 1; p <= n; p++) {
            if (!st[p]) {
                primes.add(p);
            }
        }
        return primes;
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        List<Integer> primes = getPrimesBySieve(n);
        for (Integer i : primes) {
            System.out.println(i);
        }
    }
}

欧拉筛法算法思想

思想

欧拉筛法（Euler Sieve）作为一种算法来找出所有小于或等于 n 的质数。欧拉筛法是一种改进的素数筛选法，使得每个合数只由其最小的质因数，它减少了标记合数时的重复工作，提高了效率。

步骤

下面是该方法的步骤归纳：

1. 初始化：
   • 创建一个布尔数组 st，长度为 n+1，用于标记数字是否为合数
   • 创建一个列表 primes 来存储筛选出的质数。
2. 遍历从 2 到 n 的所有整数：
   • 对于每一个整数 i，如果 st[i] 为 false（即 i 未被标记为合数），则认为 i 是一个质数，并将 i 添加到质数列表 primes 中。
3. 标记合数：
   • 使用已经找到的质数列表中的元素 p 来标记合数。对于每一个质数 p，遍历从 i*p 开始的后续合数，并将其在 st 数组中标记为 true。
   • 在标记合数的过程中，一旦 i*p 超过 n，则停止进一步的标记。
   • 另外，当 i 能够被 p 整除时（即 i % p == 0），表明 p为p * i的最小质因子，此时可以停止内部循环以避免重复标记。
4. 返回结果：
   • 完成以上步骤后，返回包含所有质数的列表 primes。
     这种筛法的关键在于减少对合数的重复标记次数，使得每个合数只由其最小的质因数来标记一次，从而提高了算法效率。

代码实现（以 java 为例）

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main {
    public static List<Integer> getPrimesByEulerSieve(int n) {
        boolean[] st = new boolean[n + 1];  // 判断是否是合数
        List<Integer> primes = new ArrayList<>();  // 存储找到的质数
        for (int i = 2; i <= n; i++) {
            if (!st[i]) {  // 如果i没有被标记为合数，则i是质数
                primes.add(i);  // 将i添加到质数列表中
            }
            for (Integer p : primes) {
                if(i*p>n)//越界
                    break;
                st[i * p] = true;  // 标记合数
                /*
                 * 确保每个合数只被它最小的质因数筛除一次
                 * 条件成立此时p为p*i的最小质因子
                 * 如合数12 当发现能被2筛去（12 = 2*6）时，此时终止循环，否则会发现仍会被3筛去（12 = 3*4）
                 */
                if (i % p == 0)
                    break;
            }
        }
        return primes;
    }
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        List<Integer> primes = getPrimesByEulerSieve(n);
        for (Integer i : primes) {
            System.out.println(i);
        }
        sc.close();
    }
}