参考博客:
https://lazzzaro.github.io/2020/05/10/crypto-crypto常用工具/
https://bbs.kanxue.com/thread-266504.htm
https://lazzzaro.github.io/2020/05/10/crypto-crypto常用算法/
工具
以windows为主
python中import gmpy2与from gmpy2 import *的区别
import gmpy2
gmpy2.gcd(a,b)
from gmpy2 import *
gcd(a,d)
gmpy2
下载:pip install gmpy2
gmpy2.mpz(n) #初始化一个大整数
gmpy2.mpfr(n) #初始化一个高精度浮点数
d = gmpy2.invert(e,n) #求逆元,de=1 mod n
c = gmpy2.powmod(m,e,n) # 幂取模,结果是 c = m^e mod n
gmpy2.is_prime(n) #素性检测
gmpy2.gcd(a,b) #欧几里得算法,最大公约数
gmpy2.gcdext(a,b) #扩展欧几里得算法
gmpy2.iroot(x,n) #x开n次根
libnum
下载:pip install libnum
libnum.gcd(a,b) #欧几里得算法,最大公约数
libnum.invmod(a,b) #求逆元
libnum.xgcd(a,b) #扩展欧几里得
libnum.s2n() #字符串转整数
libnum.n2s() #整数转字符串
libnum.s2b() #字符串转二进制
libnum.b2s() #二进制转字符串
libnum.generate_prime() #产生质数
libnum.factorize() #质数分解
pycryptodome
下载:pip install pycryptodome
bytes_to_long() #二进制串转换为长整型数字
long_to_bytes() #整型转二进制串
sympy
下载:pip install sympy
prime(n) #第n个素数
isprime(n) #素性检测
primepi(n) #小于n的素数的总数
nextprime(n) #下一个素数
prevprime(n) #上一个素数
nthroot_mod(c,e,p,all_roots=True) #有限域开方
yafu
下载:yafu分解大素数
也可以使用在线分解工具:factordb
在终端进行打开,N为要分解的数
.\yafu-x64.exe "factor(N)" // 一般模式
.\yafu-x64.exe "factor(@)" -batchfile N.txt // 待分解因数过长时,将其保存在yafu目录下文件N.txt(文件最后一行换行)中
wiener-attack
下载:维纳攻击
使用条件:e很大的时候
from RSAwienerHacker import hack_RSA
hack_RSA(e,n)
# 解得为d,在自行进行后续运算即可
Sage
定义
R.<X> = PolynomialRing(Zmod(n))
#Zmod(n):指定模,定义界限为n的环;Z表示整数;指定模是划定这个环的界限,就是有效的数字只有从0到n,其他的都通过与n取模来保证在0~n这个范围内;Zmod代表这是一个整数域中的n模环
#ZZ:整数环;QQ:有理数环;RR:实数环;CC:复数环
#R:只是一个指针,指向用polynomialring指定的那个环(可以使用任意字符)
#PolynomialRing:这个就是说建立多项式环
#.<X>:指定一个变量的意思(可以用任意字符)R.<M> = PolynomialRing(MatrixSpace(Zmod(n),3,3))
#定义一个模n的矩阵
数论
prime_pi(n) #小于等于n的素数个数
divisors(n) #n的因子
number_of_divisors(n) #n的因子数
factor(n) #n的因式分解
euler_phi(n) #n的欧拉函数值
m_squares(n) #n的m数平方组合x.nth_root(n, truncate_mode=True) #x开n次方(不管是否完全开方,取整)
mod(x,p).nth_root(n) #x有限域开n次方# x有限域开n次方,e大
def mod_nth_root(x, e, n):r, z = pari(f"r = sqrtn(Mod({x}, {n}), {e}, &z); [lift(r), lift(z)]")r, z = int(r), int(z)roots = [r]t = rwhile (t := (t*z) % n) != r:roots.append(t)return roots
多项式
f.subs({x:x1}) #把x1值代入x
f.univariate_polynomial() #映射为单变量多项式
f.univariate_polynomial().roots() #单变量多项式求根
f.coefficients() #多项式系数列表
f.padded_list(n) #多项式系数转换为长度为n的列表
f.list() #多项式系数
f.monic() #首一多项式
f.sub(x,x-1) #将x-1代入x
f.factor() #分解因式#因式分解(单元)
x = PolynomialRing(RationalField(), 'x').gen()
f = (x^3 - 1)^2-(x^2-1)^2
f.factor()#因式分解(二元)
x, y = PolynomialRing(RationalField(), 2, ['x','y']).gens()
f = (9*y^6 - 9*x^2*y^5 - 18*x^3*y^4 - 9*x^5*y^4 + 9*x^6*y^2 + 9*x^7*y^3 + 18*x^8*y^2 - 9*x^11)
f.factor()#GCD(单元)
x = PolynomialRing(RationalField(), 'x').gen()
f = 3*x^3 + x
g = 9*x*(x+1)
f.gcd(g)#GCD(多元)
R.<x,y,z> = PolynomialRing(RationalField(), order='lex')
f = 3*x^2*(x+y)
g = 9*x*(y^2 - x^2)
f.gcd(g)#多项式/整数转换
PR = PolynomialRing(GF(2),'x')
R.<x> = GF(2^2049)
pc = R.fetch_int(xx) #整数转多项式
xx = R(PR(pc)).integer_representation() #多项式转整数#拉格朗日插值
PR = PolynomialRing(Zmod(p), 'x')
f = PR.lagrange_polynomial(points)
矩阵
A = matrix(ZZ, [[1,1],[0,4]])
A.nrows() #行数
A.ncols() #列数
A.transpose() #转置
A.inverse() 或 A^(-1) #逆
A.rank() #秩
A.det() #行列式
A.stack(vector([1,2])) #矩阵后添加一行
A.augment(vector([1,2])) #矩阵后添加一列
A.insert_row(1, vector([1,2])) #在第一行插入
A.change_ring(QQ) #更换环为QQ
A.solve_left(B) 或 A/B #求解XA=B
A.solve_right(B) 或 A\B #求解AX=B
A.left_kernel() #求解XA=0,线性相关的行向量
A.right_kernel() #求解AX=0,线性相关的行向量
A.LLL() #最短正交基
A.multiplicative_order() #乘法阶matrix.zero(2,3) / zero_matrix(2,3) #2*3零矩阵
matrix.identity(2) / identity_matrix(2) #2*2单位阵
block_matrix(QQ,[[A,zero_matrix(n,1)],[matrix(b),matrix([1e-16])]]) #矩阵拼接
解方程
以二元一次方程为例:
var('x y')
solve([x+y==10,x*y==21],[x,y])
解线性方程组
以AX=B为例:
A = Matrix([[1,2,3],[3,2,1],[1,1,1]])
Y = vector([0,-4,-1])
X = A.solve_right(Y)
#或
A \ Y
#反斜杠 \ 可以代替 solve_right; 用 A \ Y 代替 A.solve right(Y).
求逆元
d = inverse_mod(e,fn)
扩展欧几里得算法
d,u,v=xgcd(20,30)
print("d:{0} u:{1} v:{2}".format(d,u,v)) #d:10 u:-1 v:1
中国剩余定理/孙子定理(RCT)

#仅适用模两两互素
def chinese_remainder(modulus, remainders):Sum = 0prod = reduce(lambda a, b: a*b, modulus)for m_i, r_i in zip(modulus, remainders):p = prod // m_iSum += r_i * (inverse_mod(p,m_i)*p)return Sum % prod
chinese_remainder([3,5,7],[2,3,2]) #23
离散对数

#n为合数(Pohlig-Hellman)
x = discrete_log(mod(b,n),mod(a,n)) #n为质数或质数幂(线性筛Index Calculus)
R = Integers(99)
a = R(4)
b = a^9
b.log(a)x = int(pari(f"znlog({int(b)},Mod({int(a)},{int(n)}))"))
x = gp.znlog(b, gp.Mod(a, n))
欧拉函数
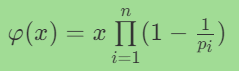
print(euler_phi(71)) #70
整数域椭圆曲线
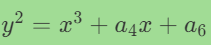
输出所有整数点:
#素数域
F = GF(7)
#素数域的阶
print(F.order())
#椭圆曲线E7(2,3)
E = EllipticCurve(F,[0,0,0,2,3])
#基点坐标
G = E.gens()[0]
#阶(不同的离散的点个数)
q = E.order()
#所有的点
allPoints = E.points()
#创建点
P = E(2,1)
#点的xy坐标值
P.xy()#倍数点
Q = k*P
Q.division_points(k) # 结果为P
曲线
# 查亏格(Genus)
x, y = ZZ['x, y'].gens()
eq = x ^ 3 + y ^ 3 + 1 - d * x * y
Curve(eq).genus() # Genus=1为椭圆曲线# 映射
# solve x^3+y^3+z^3=d*x*y*z
R.<xx,yy,zz> = Zmod(p)[]
cubic = xx^3 + yy^3 + zz^3 - d * xx * yy * zz
EC = EllipticCurve_from_cubic(cubic, morphism=False) #映射的椭圆曲线
mf = EllipticCurve_from_cubic(cubic, morphism=True) #映射关系
P =
PP = mf(P)
解模方程
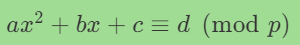
P.<x> = PolynomialRing(Zmod(p))
f = a * x^2 + b * x + c - d
x = f.monic().roots()
print(x)
解方程组
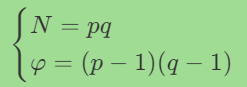
P.<p, q> = PolynomialRing(ZZ)
def solve(f1, f2):g = f1.resultant(f2, q)roots = g.univariate_polynomial().roots()if len(roots) == 0:return Falsep_ = abs(roots[0][0])q_ = abs(roots[1][0])return (min(p_, q_), max(p_, q_))N =
phi =
f1 = (N + 1) - phi - p - q
f2 = N - p*q
p, q = solve(f1, f2)
(p, q)