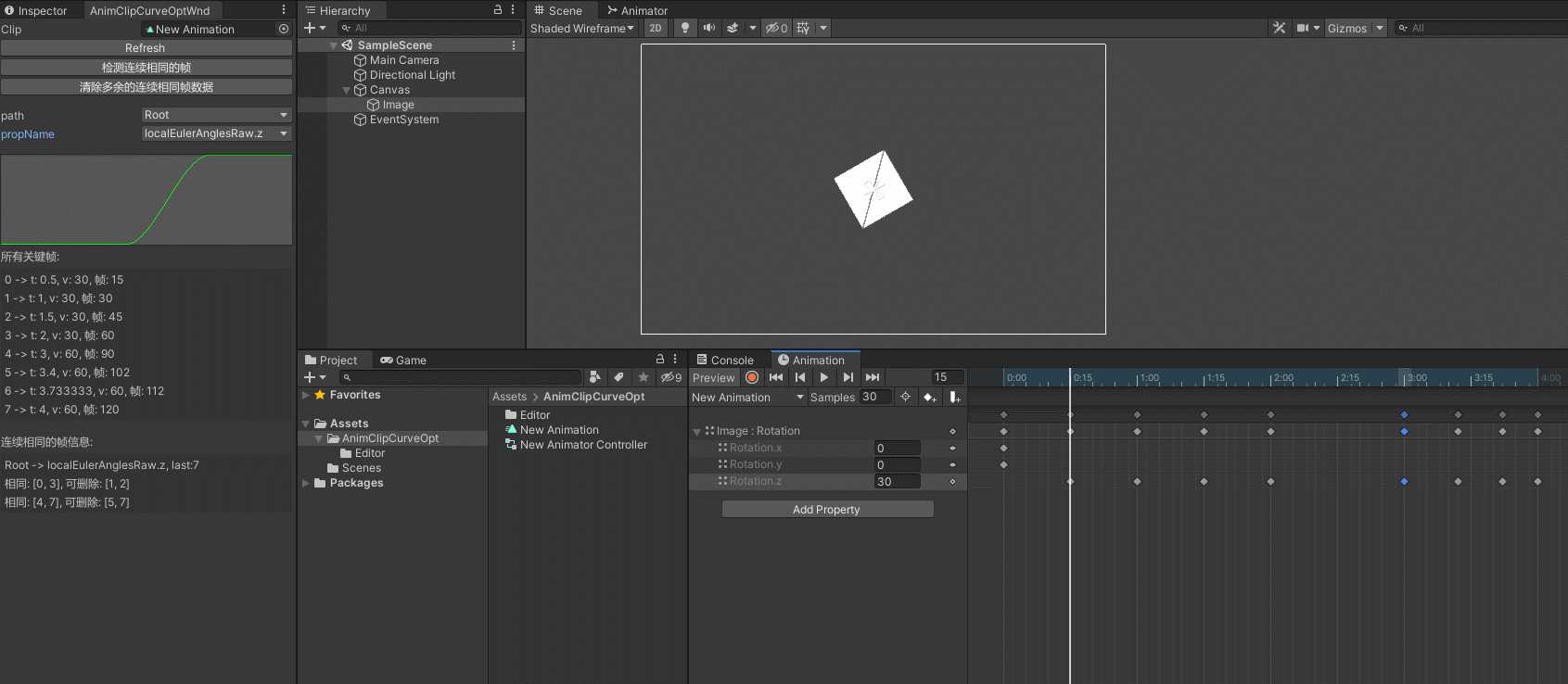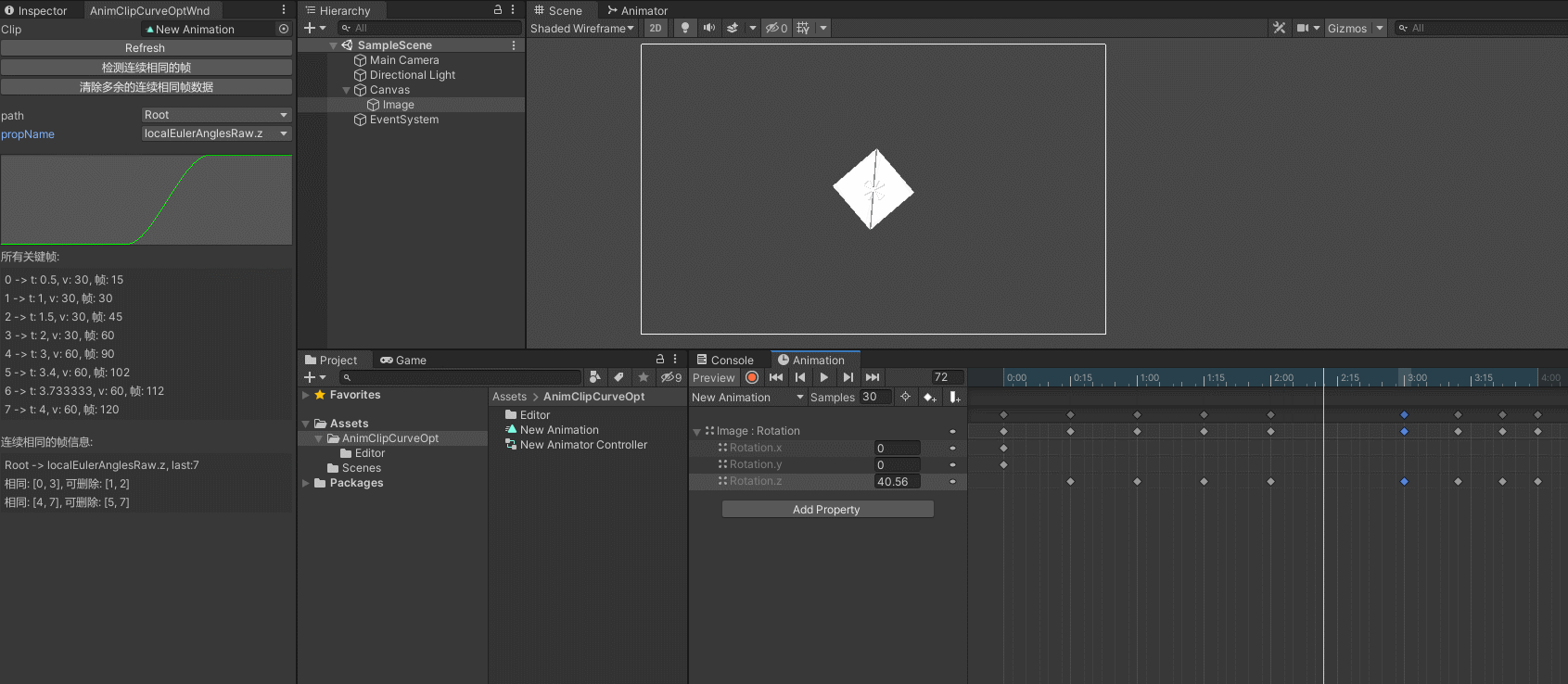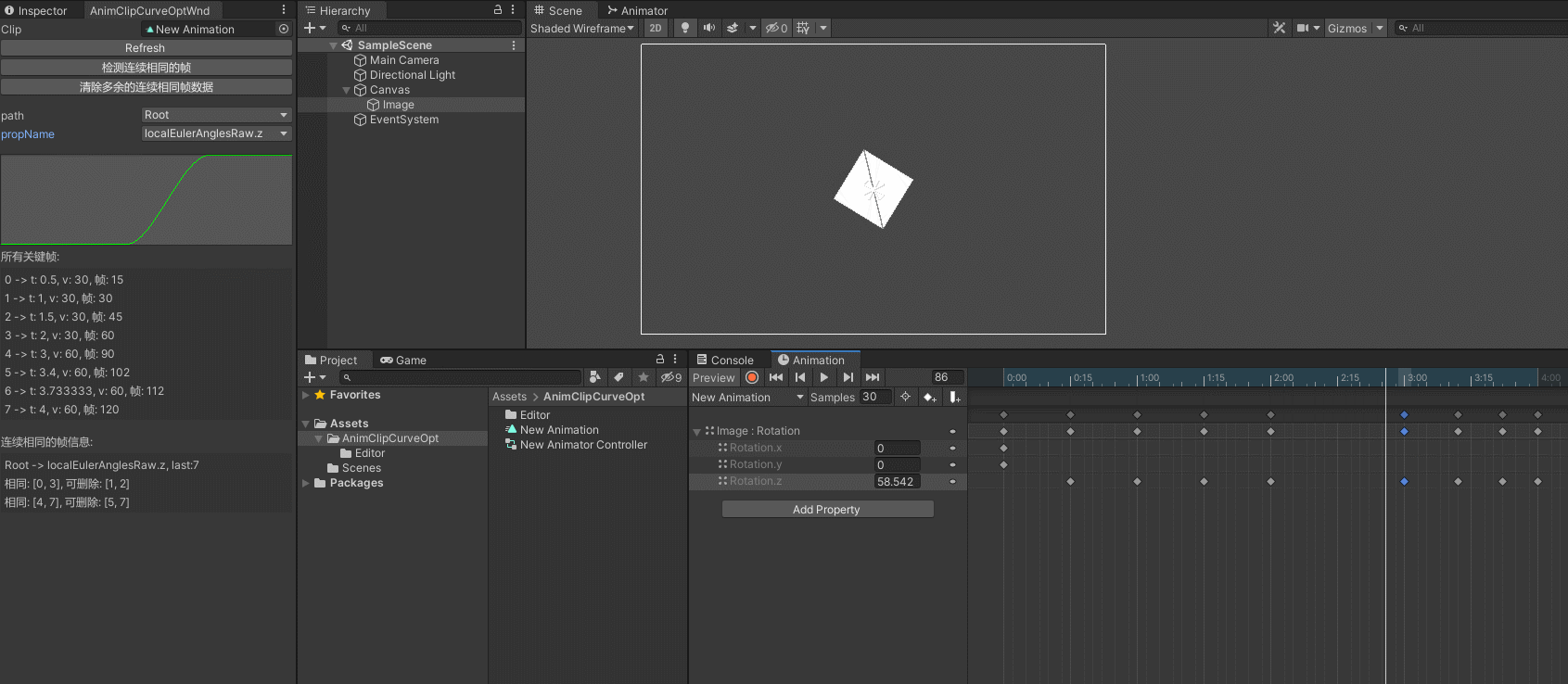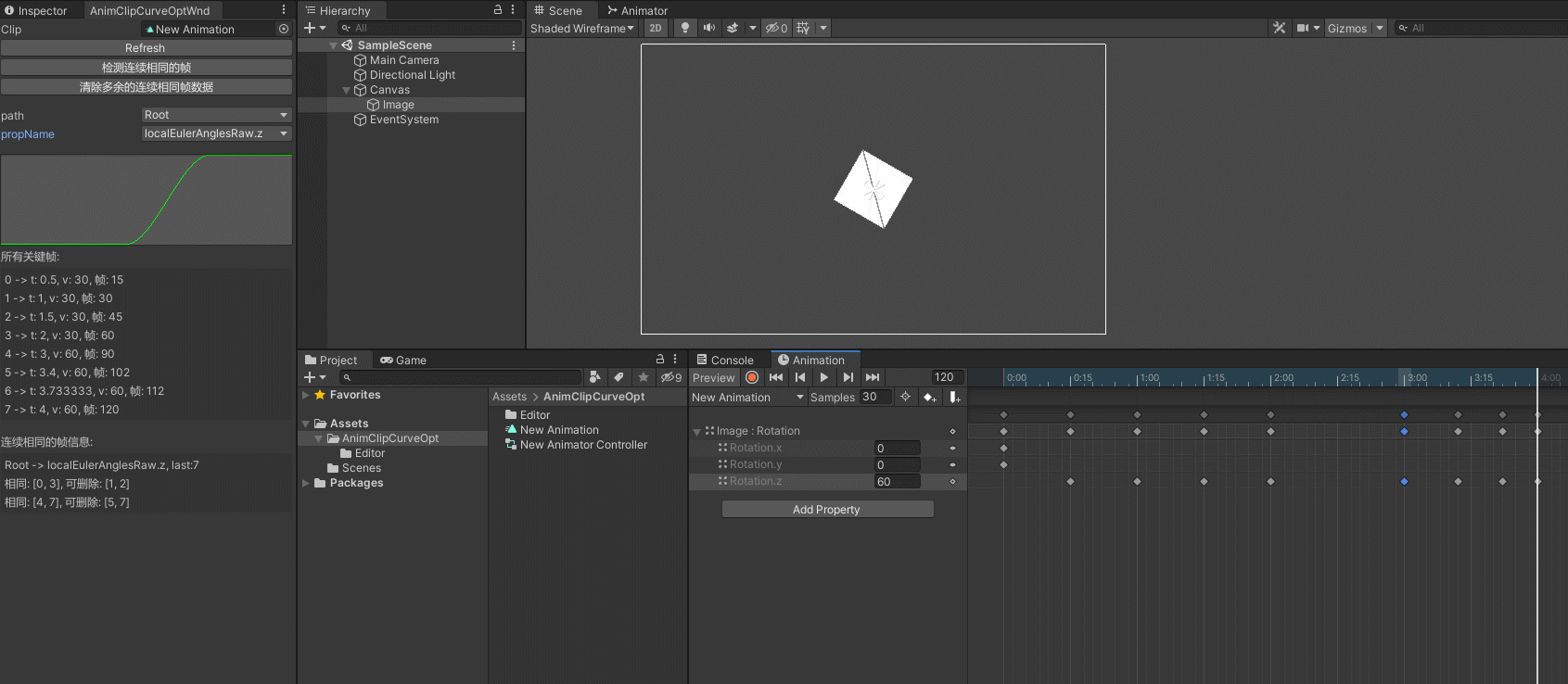
15 发现阿基米德公式
在前面的课程中,我们揭示了一些微积分关系,即系统如何变化的 “算术”:

这些规则对我们有什么帮助?
- 如果我们已经有了一个等式,那么这些规则就是我们找到逐步模式的捷径。幂次法则让我们不再把一个增长的正方形或立方体看成是一个图形,而是让我们通过x2和x3。无论x^2是指一个正方形,还是仅仅指乘方--我们可以得到变化的模式。
- 如果我们有一组变化,这些规则就能帮助我们逆向推导出原始模式。
学会用微积分来思考,意味着我们可以用 X 光和延时视觉来想象正在发生的变化,并用规则来计算出具体细节。最终,我们可能什么都不用想象,直接用符号来计算(就像你今天做算术题一样)。
在课程开始时,我们将环形变为圆形,然后是球形,最后是贝壳形:
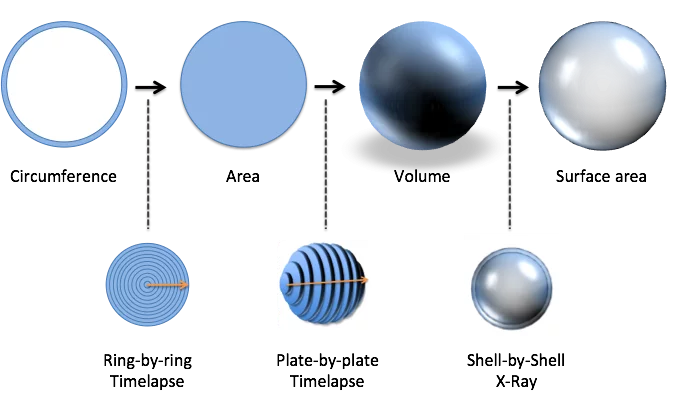
有了正式的规则,我们就可以快速通过计算,自己找到圆/球公式。这听起来可能有点奇怪,但当你看到这些公式在你面前变形时,我觉得它们与众不同,几乎是活的。让我们开始吧。
15.1 将圆周长改为面积
我们第一个 “循序渐进 ”思考的例子是将一连串的圆环粘成一个圆:

开始时,我们需要大量的可视化。我们必须展开圆环,将它们排成一行,意识到它们组成了一个三角形,然后用
来计算面积。直观、乏味......但很有必要。在使用原始方程之前,我们需要感受正在发生的事情。
我们一起来看看。从 “逐环延时 ”的概念到 “整合各环,从无到全半径”,最终:
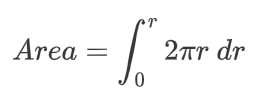
我们希望将这些面积累积起来,形成我们的圆盘。
如何求解这个等式呢?通过逆向思维。我们可以将
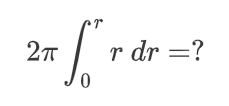
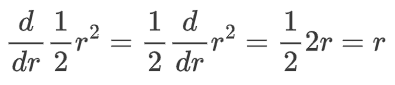
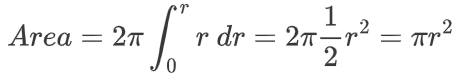
参考资料
- 软件测试精品书籍文档下载持续更新 https://github.com/china-testing/python-testing-examples 请点赞,谢谢!
- 本文涉及的python测试开发库 谢谢点赞! https://github.com/china-testing/python_cn_resouce
- python精品书籍下载 https://github.com/china-testing/python_cn_resouce/blob/main/python_good_books.md
- Linux精品书籍下载 https://www.cnblogs.com/testing-/p/17438558.html
15.2 将面积转化为体积
让我们更进一步。我们可以把圆片加厚成板,然后构建一个球体:

让我们慢慢来。我们有几个板,每个板的 “X 坐标 ”都不同。单个圆板的大小是多少?
板有厚度dx和自己的半径。板的半径是它从 x 轴出发的高度,我们可以把它叫做y。
.
一开始有点混乱: r是整个球体的半径,但y是被测板的半径(通常较小)。事实上,只有中心板 (x=0)的半径与整个球面的半径相同。
根据勾股定理,我们可以将平板的x位置与其高度y联系起来: x^2 + y^2 = r^2
好的。我们有了每块板的尺寸,就可以积分求体积了,对吗?
没那么快。与其从左边的负 x 坐标开始,移动到 0,然后再移动到最大值,不如把球体看成两个半球:

求总体积时,先求出一半的体积,再将其翻倍。这是一个常见的技巧:如果一个形状是对称的,就先求出其中一部分的大小,然后将其放大。通常,计算 “0 到最大值 ”比计算 “最小值到最大值 ”更容易,特别是当 “最小值 ”为负数时。
好的。现在让我们来解决它:

哇哦 好大一个方程。虽然看起来很多,但我们还是要解决它:
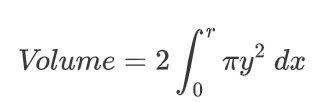
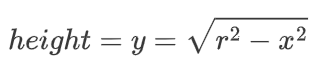
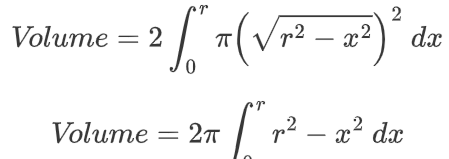
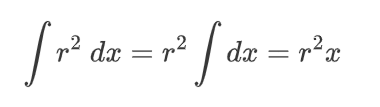
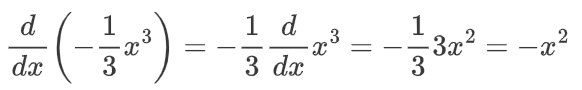
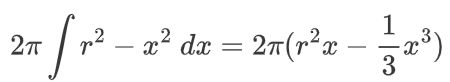
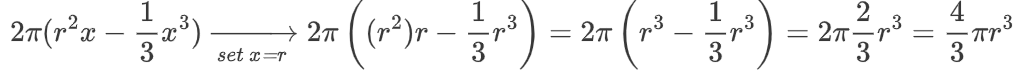
觉得这很难吗?你根本想不到。阿基米德是有史以来最伟大的天才之一,他花了巨大的精力才计算出这一行。他必须想象一些球体、一个圆柱体、一些圆锥体和一个支点,想象它们之间的平衡,然后......这么说吧,当他发现这个公式时,他把它写在了自己的坟墓上。
15.3 将体积转化为表面积
有了体积,求表面积就容易多了。我们可以用逐壳 X 射线对球体进行薄薄的 “剥离”:
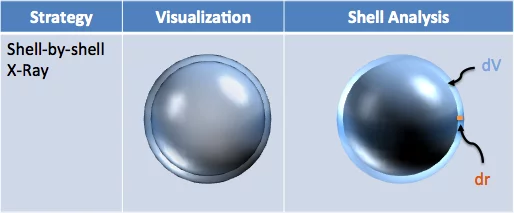
我把整个外壳想象成现有球体表面的 “粉末”。有多少粉末?是dV体积的变化。好吧,粉末覆盖的面积是多少?
嗯。想想类似的问题:一袋地膜覆盖多少面积?得出体积,除以所需的厚度,就得出了覆盖面积。如果我给你 300 立方英寸的泥土,并把它铺成 2 英寸厚的土堆,那么这堆泥土将覆盖 150 平方英寸的面积。毕竟,如果 Area * Thickness = Volume, 那么 Area = Volume / Thickness。
.
在我们的例子中dV是外壳的体积, dr是厚度。我们可以将 dV沿着我们考虑的厚度 dr ,看看我们增加了多少面积: dV/dr。
这时,正确的符号就派上用场了。我们可以把导数看作抽象的瞬时变化率( V`),也可以看作具体的比率(dV/dr)。
. 在这种情况下,我们要考虑的是各个元素以及它们之间的相互作用(壳体体积/壳体厚度)。
因此,根据以下关系
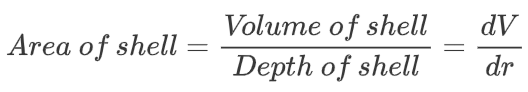
我们可以算出

哇,速度真快!我们可以尝试将圆周率直接转化为表面积,但这比较复杂。
在计算公式的过程中,我们 “去掉 ”了r3得到3r2 .
15.4 2000 年的数学一日千里
我们所研究的步骤是经过 2000 年的思考才发现的,而且是由最伟大的天才们发现的。微积分的视角如此宽广,令人叹为观止,很难想象它在哪里不适用。这就是利用 X 射线和延时视觉:
- 将事情分解。在你目前的情况下,接下来会发生什么?之后呢?这里有什么规律吗?(变大、变小、不变)这些知识对你有用吗?
- 找到源头。你看到了一系列变化--是什么导致了这些变化?如果你知道源头,你能预测所有变化的最终结果吗?这种预测有用吗?
我们习惯于分析方程式,但我希望不要止步于此。数字可以描述情绪、辣度和客户满意度;逐步思考可以描述作战计划和心理治疗。方程和几何只是分析的良好起点。数学与方程无关,音乐与乐谱无关--它们指向的是符号内的思想。
虽然还有更多关于其他导数、积分技巧和无穷大原理的细节,但你并不需要它们来开始微积分的思考。你今天的发现会让阿基米德热泪盈眶,这对我来说已经是一个很好的开始了。