mount
我们会惊奇的发现,无论网格在哪里,只要有山覆盖了,那么这里的贡献一定是 \(\sqrt{2}\),如下的图可以证明:
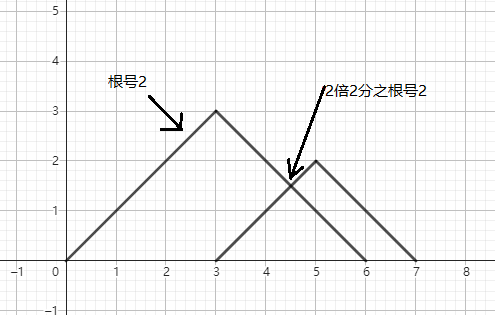
那么我们就只用开一个线段树,维护的是最小值和最小值的出现次数,如果最小值不为 \(0\),那么这部风就没有贡献,反之贡献就要加上最小值的出现次数
细节
由于我们可以直接把山峰转换成 \([max(0ll, x - y), min(w, x + y)]\),但是由于取了个 \(min\) 和 \(max\) 有可能把两座山峰判成同一组,所以我们还要记录最开始的 \(x, y\)
nac
我们可以发现,设 \(a, b, c\) 分别表示当前子序列 \(N, NA, NAC\) 的出现次数,那么我们可以得到如下代码
for (int i = 1; i <= n; i++) {if (s[i] == 'N') {a++;}else if (a[i] == 'A') {b += a;}else if (a[i] == 'C') {c += b;}
}
那么我们可以设状态 \(dp_{i, j, k}\) 表示当前有几个为 \(N, NA, NAC\),那么我们可以记上一次的转移,最终递归输出即可