问题引出:
给出 \(n\) 个点的树,求出分别以不同的 \(i\) 为根时,所有结点深度的和,根节点的深度为 \(0\)。
首先我们有个自然的暴力思路, 也就是以每个节点为根节点做一遍 \(dfs\) 这样的复杂度是 \(O(n^2)\) 级别的, 所以要进行优化
看下图:
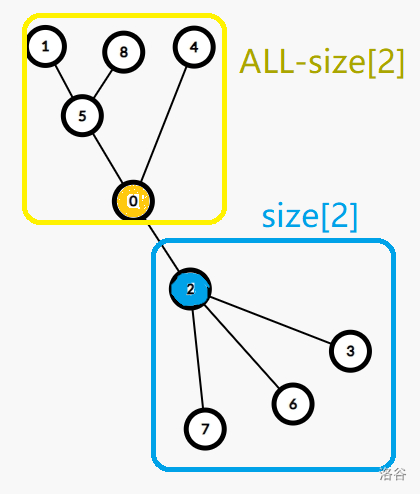
我们首先假设每个节点具有点权, 明显这里的点权是 \(1\), 接着给出以下定义:
- 定义 \(c_i\) 为点权, 这里为 \(1\)
- 定义 \(ALL\) 为所有点权的和
- 定义 \(size_u\) 为以 \(u\) 为根的子树内的点权和
假设我们此时以及求出了 \(0\) 号节点的答案 \(dp_0\), 那么当我们要求 \(2\) 号节点时, 我们把这个树分成两部分, 很明显黄框框出的部分内部的所有的节点到根节点的距离都要增加一个 \(w_{0 → 2}\), 这里明显边权为 \(1\), 那么其答案应该增加 \((ALL - size_2) * w_{0→2}\) , 接着看红框部分, 明显的所有的节点距离根节点的都要减去边权, 所以答案还应该减去 \(size_2 * w_{0→2}\), 故 \(dp_2 = dp_0 + ALL - size_2 - size_2\), 同理可以递推出其它的节点, 时间复杂度为 \(O(n)\)
代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
signed main()
{std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n; cin >> n;int sum = 0;vector<int> c(n + 1);for(int i = 1; i <= n; i++) c[i] = 1, sum += c[i];vector<pair<int, int>> g[n + 1];for(int i = 1; i < n; i++){int a, b; cin >> a >> b;g[a].push_back({b, 1}), g[b].push_back({a, 1});}vector<int> dp(n + 1), sz(n + 1), dep(n + 1);function<void(int, int)> dfs1 = [&](int u, int fa) -> void{dp[1] += c[u] * dep[u], sz[u] = c[u];for(auto [x, y] : g[u]){if(x == fa) continue;dep[x] = dep[u] + y;dfs1(x, u);sz[u] += sz[x]; }};function<void(int, int, int)> dfs2 = [&](int u, int fa, int cur) -> void{dp[u] = cur;for(auto [x, y] : g[u]){if(x == fa) continue;int ndp = cur;ndp += (sum - sz[x]) * y - sz[x] * y;dfs2(x, u, ndp);}};dfs1(1, 0), dfs2(1, 0, dp[1]);for(int i = 1; i <= n; i++) cout << dp[i] << '\n';return 0;
}
变形题目
1. Minimize Sum of Distances
Minimize Sum of Distances
此时的点权就要变了, 但是其目的还是一样的, 按照我们的模板改一下点权就可以了, 此题还可以用重心来做, 直接求出重心也是可以的
重心代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
signed main()
{std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n; cin >> n;vector<int> g[n + 1];for(int i = 1; i < n; i++){int a, b; cin >> a >> b;g[a].push_back(b), g[b].push_back(a);}int sum = 0;vector<int> c(n + 1);for(int i = 1; i <= n; i++) cin >> c[i], sum += c[i];int res = 0, root = 0;vector<int> dp(n + 1), ndp(n + 1);dp[0]= 1e18;function<void(int, int)> dfs1 = [&](int u, int fa) -> void{dp[u] = 0, ndp[u] = c[u];for(auto x : g[u]){if(x == fa) continue;dfs1(x, u);ndp[u] += ndp[x];dp[u] = max(dp[u], ndp[x]);}dp[u] = max(dp[u], sum - ndp[u]);if(dp[u] < dp[root]) root = u;};function<void(int, int, int)> dfs2 = [&](int u, int fa, int d) -> void{for(auto x : g[u]){if(x == fa) continue;dfs2(x, u, d + 1);res += c[x] * d;}};dfs1(1, 0), dfs2(root, 0, 1);// for(int i = 1; i <= n; i++) cerr << dp[i] << ' ' << ndp[i] << endl;cout << res << '\n';return 0;
}
换根 \(dp\) 代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
signed main()
{std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int n; cin >> n;vector<int> g[n + 1];for(int i = 1; i < n; i++){int a, b; cin >> a >> b;g[a].push_back(b), g[b].push_back(a);}int sum = 0;vector<int> c(n + 1);for(int i = 1; i <= n; i++) cin >> c[i], sum += c[i];vector<int> dp(n + 1), sz(n + 1);function<void(int, int, int)> dfs1 = [&](int u, int fa, int d) -> void{dp[1] += c[u] * d, sz[u] = c[u];for(auto x : g[u]){if(x == fa) continue;dfs1(x, u, d + 1);sz[u] += sz[x]; }};function<void(int, int, int)> dfs2 = [&](int u, int fa, int cur) -> void{dp[u] = cur;for(auto x : g[u]){if(x == fa) continue;int ndp = cur;ndp += sum - sz[x] * 2;dfs2(x, u, ndp);}};dfs1(1, 0, 0), dfs2(1, 0, dp[1]);cout << *min_element(dp.begin() + 1, dp.end()) << '\n';return 0;
}
下面的题只需要改改边权改改点权就可以了
2.[USACO10MAR] Great Cow Gathering G
[USACO10MAR] Great Cow Gathering G
3.Distance Sums 2
Distance Sums 2
4.Tree with Maximum Cost
Tree with Maximum Cost
5.[POI2008] STA-Station
[POI2008] STA-Station
6.Tree Painting
Tree Painting
7.「MXOI Round 1」城市
「MXOI Round 1」城市