第一章
1.1 流体的概念
任何固体材料都有一个强度极限,即使合外力和力矩都为零,它的内部也可能会存在着拉力、压力或者剪切力。当这些内应力超过了材料的强度极限时,固体就会被破坏,从而产生运动。微观上体现为断裂处的分子(或原子)之间的化学键被破坏,失去了相互的作用力,不再能保持原有结构形式了。
流体的内部只存在压应力时,可以和固体一样产生变形并保持静止。当流体内部存在剪切力时,会产生剪切变形,但这种剪切变形完全产生不了相应的剪切力。于是在剪切力的作用下流体将不断地变形下去,只要剪切力存在,就不会停止。这种情况有点类似于固体受力远超过其强度的情况,只不过流体对于剪切力没有任何“强度”可言,任何小的剪切力都将使其不断变形下去。因此,流体与固体的本质区别是:流体仅仅依靠静止变形是无法在内部产生剪切应力的。
流体在运动状态下内部是可以产生剪切力的。流体的这个性质称为粘性。
1.2 流体性质
流体的很多性质是与固体中的定义相通的,比如密度、压力、温度等。但也有其独特的属性,这里面最典型的就是区分流体和固体的力学特性──粘性。此外,液体具有表面张力、气体具有易压缩性,这些都是流体特有的属性。
1.2.1 流体的粘性
流体受到外界的剪切力作用的时候,它会不断地变形下去,在这种连续的剪切变形作用下的流体内部会产生剪切应力,这种性质称为流体的粘性。我们通常见到的液体和气体都有粘性,只有超流体可以认为是没有粘性的。
当流体与固体相接触时,紧挨着固体的流体分子会被吸附在固体上随之运动。因此,所谓流体与固体之间的摩擦力其实也就是流体之间的摩擦力。
摩擦力为什么和挤压力呈正比呢?
毕竟挤压力与摩擦力是垂直关系,应该没有沿摩擦力方向的分量才对。原因是这样:挤压力越大,则两物体的接触面积就越大,这个接触面积与挤压力之间基本上是线性关系,因此摩擦力也与挤压力呈正比。如果是分子级别光滑的两个物体相接触,则摩擦力就基本上与挤压力无关了。
液体与固体的接触是分子级别的全面接触,因此摩擦力应该与挤压力无关。这个挤压力就是指流体内部的压力(本书中若非特别强调,压力都是指压强,即单位面积上的压力),这可以解释为什么液体的粘性力大小基本与压力无关。但流体的粘性力大小与温度却有着极大的关系,我们都知道凉的糖浆较粘稠,加热后粘性降低,一般对于液体来说温度越高粘性力越小。气体的粘性力较小,生活中一般较难察觉,但精密的实验已经证实,与液体相反,对于气体来说温度越高粘性力越大。液体和气体粘性的这些特性与产生粘性的物理本质是直接相关的,既然这两者不同,就应该分别加以分析。
上面讨论的由分子力引起摩擦力的作用与固体有些类似,实际上对于液体的摩擦力来说还有一个不同于固体的作用,那就是液体分子并不会安分地分层流动,而是会互相扩散。也就是说各层的分子会有与运动方向垂直的横向运动,上层的分子会跑到下层去,下层的分子也会跑到上层去。这样,上层的分子进入下层后就会推动下层的分子运动得快一些,而下层的分子跑到上层去后会拖累上层分子使之速度减慢。这种作用也可以解释为两层之间的动量传递,既然是沿运动方向的动量传递,就有沿这个方向的力,这个力就是摩擦力。
对于做层流运动的液体而言,这个作用远小于前述的分子吸引力和排斥力的作用,因此经常可以忽略,而认为液体的粘性就是由分子力造成的,其中吸引力经常是主要的。
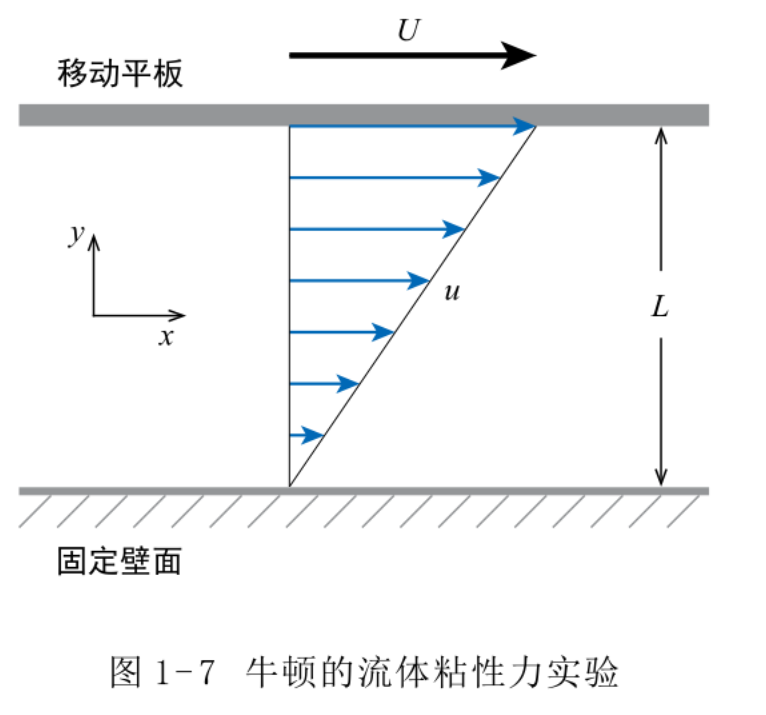
图 1-7中,下面的壁面保持静止,上面的平板以水平速度运动。鉴于流体在与固体壁面接触的地方会依附在固体表面,与下壁面接触的流体保持静止,与上平板接触的流体以速度 U 随之运动。牛顿根据实验结果总结出的规律是:上平板所需的拖动力与其运动速度成正比,与两平板间的距离成反比,即
式中,F 为拖动平板的力;A 为平板和流体的接触面积;U 为上平板的运动速度;L 为两平板间的距离。
鉴于实验时流体左侧和右侧的压力相同,因此平板给予流体的 x 向拖动力在各层流体之间都是相同的,这样就可以得到任意两层流体之间的切应力。实验中还发现流体速度沿 y 方向呈线性分布,因此牛顿得到:平行流动中,任意两层流体之间的切应力可以写为
式中,τ 为切应力;u 为流体水平方向的速度;y 为垂直方向的坐标;μ 是一个描述流体粘性大小的系数,称为粘性系数,有时称为动力粘性系数。μ 就是流体粘性大小的度量,不同流体的粘性系数差别很大,同一种流体的粘性系数则基本上只随温度变化。
事实上并不是所有的流体都遵循式(2),牛顿实验所用的流体是满足这个关系的,基本上所有气体和粘性小的液体都是满足这个关系的,这些流体被大家称为牛顿流体。因为这种流体的切应力与速度梯度之间是线性关系,因此有时也称为线性流体。
自然界中也存在着大量不满足式(2)的流体,这一类流体统称为非牛顿流体。一般来说,牛顿流体的粘性比较小,那些粘性比较大的诸如油漆、蜂蜜、血液等基本上都属于非牛顿流体。可以看出非牛顿流体一般对应着大分子的液体,这些液体的分子在有速度梯度的流场中会互相纠缠,因此粘性力与速度的关系更复杂些。所有非牛顿流体的切应力与速度梯度都不是线性关系,有些非牛顿流体的剪切力不但与速度相关,还与作用时间长短相关。
1.2.2 液体的表面张力
表面张力是使液体表面收缩的一种力,是表层分子之间相互吸引产生的。分子间力称为范德华力,同时包含吸引力和排斥力。当液体不受外力时,内部分子间也处于平衡的不受力状态,即吸引力和排斥力相等,分子们靠近一点就体现出排斥力,远离一点就体现出吸引力。而在液体表面上,经常有些能量高的分子挣脱了其他分子的吸引力而逃脱,这就是液体的气化。在这种作用下,液体表层分子间的距离比内部分子间的距离更大一些,分子间体现为拉力,这就是表面张力。表面张力的存在使液体表面趋向于面积最小,使液滴倾向于呈球形。
1.2.3 气体的状态方程
由热力学可知,气体的压力、密度和温度三者之间满足一定的关系,这种关系称为状态方程。如果气体分子本身的体积和分子之间的作用力可以忽略,这种气体就称为完全气体(又称理想气体),其状态可以用下式来表示,即
式中,\(p\) 为压力;\(\rho\) 为密度;\(T\)为温度;\(R_0\)为理想气体常数,\(R_0=8.314\)J/(mol\(\cdot\)K); \(M\)为气体的摩尔质量(需要用 kg 表示以适应其他量的国际单位)。
多数气体在常见的压力和温度范围内的分子自由程都比较大,因此都是比较符合完全气体状态方程的,在流体力学中处理的气体主要是空气,其状态方程常简写为
式中,R称为气体常数,对于空气, R=287.06 J/(kg ·K)。
不同于气体,液体的状态方程并没有一个统一的理想模型存在。一般的液体密度随温度升高而降低,变化率各有不同,是由很多因素决定的,很难用统一的理论描述,一般用实验确定。水是一种比较特殊的液体,在 4℃时密度最大,低于或高于这个温度时密度都会减小。液体的压力则基本上与温度和密度无关,主要取决于所受的外力。流体力学中一般把液体当做不可压缩流体对待,即液体的密度不随压力而改变,而压力和温度分别由动量方程和能量方程决定。
1.2.4 气体的压缩性
压缩性是指对于一定量的物质其体积的改变程度,或者其密度的改变程度。固体和液体的分子紧密地挤在一起,任何妄图让它们更靠近一些的努力都将会受到巨大的分子间排斥力的反抗,因此固体和液体都是很难压缩的。
决定物质是否会被压缩的因素不只是它本身的抗压能力,还要看其受力的大小。实际上虽然气体较易压缩,但对于多数流动问题,气体微团的受力都远未达到明显影响其自身体积的程度,从而可以忽略压缩性的影响。例如,一辆汽车以120 km/h的速度行驶时,其前面“撞上”的空气只会受到非常轻微的压缩(密度改变不到 0.5%),然后就四散流动开来。这种压缩的本质是气体在减速过程中惯性力对自身的作用,因此这类流动中气体的密度与其流动速度直接相关。一般认为气体在低于 0.3倍声速的流动中密度变化很小,可以按不可压缩处理,当然根据要求精度的不同,这个标准也可以适当提高或降低。
惯性力除了可由速度的大小改变产生外,也可以由速度的方向改变产生。在高速旋转的容器中,不同旋转半径处的气体会有不同的压力,对应着不同的密度。这时即使气体以缓慢的速度从中心流向四周,密度也会有明显的改变,这种压缩作用是离心力造成的。
除了惯性力外,重力对气体密度也会有影响,比如不同高度的大气密度有明显的不同。一般在高度差不大的情况下,重力的影响并不大,例如,我们认为十层楼高处的空气与地面处的空气密度是一样的,实际上它们有千分之几的差别。如果要处理气体由地面上升到云端的流动,恐怕就必须要考虑重力带来的压缩影响了。
温度变化对密度的影响也不可忽略,如果气体微团在流动过程中对外传热,那么其自身温度降低,此时就会受到压缩,接受来自外界的压缩功。反之,如果气体微团在流动过程中接受外界的热量,那么其自身温度升高,此时就会膨胀,对外界做膨胀功。
若流体是不可压缩的,则没有压缩功和膨胀功的存在,温度对流动的影响就会小得多,这时的流动问题会得到极大的简化。因此,对于温差不太大,离心力不太强,速度不高的气体流动来说,可以假设流体是不可压缩的,这称为不可压缩流动理论。这种流动是流体力学中研究得最多,应用也最为广泛的流动。
1.2.5 气体的导热性
热量在物体中会由温度高的地方传向温度低的地方,这种性质称为导热性。单位时间单位面积所传递的热量由傅里叶定律确定,即
\(\dot{q}\)为单位时间内通过单位面积的传热量;λ 为物质的导热系数;n 为温度梯度的方向。
气体中的导热与固体中的导热机理有很大不同,固体分子平均位置不动,分子动能的传递靠的是分子的振动,气体中的导热还包括分子热运动的扩散效应。扩散效应并不等同于流动中的掺混作用,因为气体的宏观速度为零时也一样存在扩散产生的导热,而气体通过宏观运动的掺混引起热量交换属于对流换热。可以看出,气体的导热性与粘性的物理本质类似,其导热系数是随温度的升高而增大的。尽管气体的导热有扩散效应在帮忙,因分子间距大,其导热能力还是要远远低于固体和液体,以至于经常可以忽略。
1.3 连续介质
物质都是由基本粒子构成的,前面的分析中大量使用了分子和原子的概念。然而对于经典的固体力学和流体力学而言,去研究单个分子或原子的行为是没有必要的。即使是对于气体这样分子间距较大的物质,也可以用压力和温度等宏观特性来描述其微观力学行为。
因此,经典力学总是把物质看作是连续可分的,称为连续介质假设,固体力学和流体力学都属于连续介质力学。
判断连续介质假设是否适用的唯一标准就是所研究的流动问题的尺度与分子大小(固体和液体)或分子自由程大小(气体)的关系。对常温常压的气体而言,分子平均自由程量级为 \(7×10^{-5} mm\),只要研究的对象远大于这个尺度,就满足连续介质假设。一般我们所见的流动满足连续性假设都没问题,像花粉颗粒这么小的尺度就不满足连续介质假设,其在静止的水中会产生布朗运动这类受水分子影响的运动。在 120km的高空运动的火箭和飞船也不满足连续性能假设,因为此处空气分子的平均自由程达到了 0.3m。
1.4 流体中的作用力
流体力学中习惯按照作用形式将物体受到的作用力分为两类:一类是不需要接触,作用于全部流体上的力,称为体积力或质量力;另一类是直接与物体相接触而施加的力,称为表面力。
重力(万有引力)和磁力都属于体积力,如果分析问题时采用非惯性坐标,则惯性力也是一种体积力。压力和粘性力都属于表面力,压力是正应力,就是说流体中任何表面上的压力都与该面垂直。流体内部的切应力完全由粘性力产生,而正应力中也有粘性力的贡献。在多数情况下,粘性正应力比起压力来说小到可以忽略,所以通常认为粘性只产生切应力。
在静止的流体中或者运动的无粘流体中,任一点的压力大小与其作用方向无关。这个性质使流体的压力具有标量属性,可以看作是流体的一种状态参数。我们可以这样理解压力与方向无关的特性:对于静止的或者运动的无粘流体,压力是唯一的表面力。对流体中的某一点而言,体积力(重力和惯性力)趋向于零,来自四面八方的表面力之间要达成平衡,就必须全部相同。
第二章
2.1 流体静止时的受力分析
流体的静止状态指的是流体各部分之间没有相对运动,或者说流体的形状不发生改变。根据流体的定义可知,这时粘性完全不发生作用,流体中的表面力只有压力,因此流体静力学的核心问题就是压力与体积力的平衡关系。因为体积力一般为重力和惯性力,所以静力学的问题主要分两类:一类是重力场中静止的流体的问题;另一类是流体不变形地做变速运动的问题。
对于任何一个静止的处于其他微团包围之下的流体微团而言,四周流体给予它的表面力(压力)之和必然和它所受的体积力相互抵消。在直角坐标系中,压力产生的合力沿任一坐标方向的投影都与那个方向的体积力大小相等方向相反。下面我们将针对一个流体微团进行分析,并导出一般形式的关系式。
如图 2-1所示,在静止的流体内部取一个六面体,让其六个面分别垂直于 3个坐标轴。3个方向的边长分别为 dx,dy 和 dz,于是该六面体的体积为dxdydz,质量为 ρdxdydz。如果用 F b 表示体积力,用 f b 表示单位质量的体积力,则有如下关系式:
在直角坐标系中,上式可以写成分量形式,即:
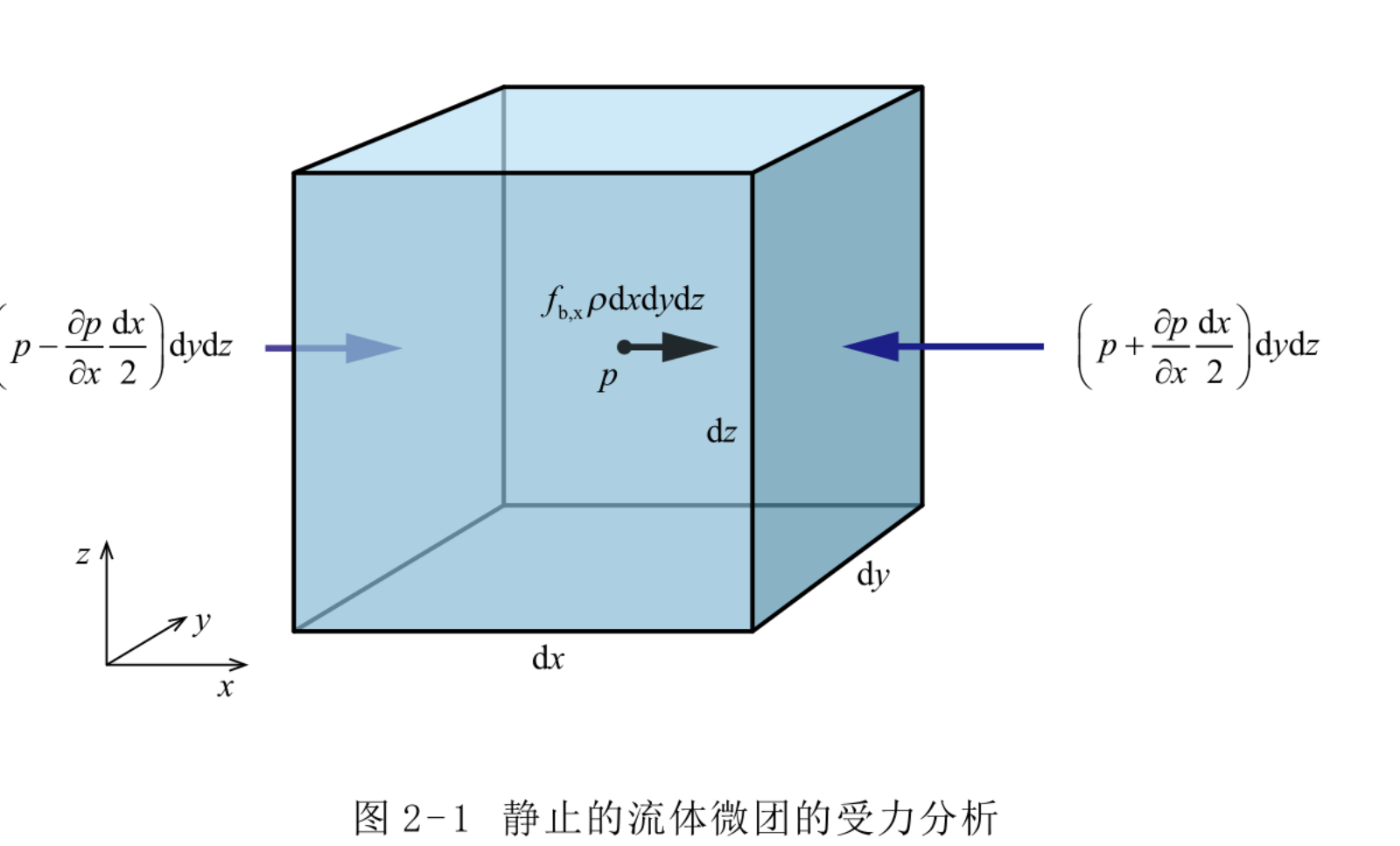
与体积力平衡的压力具有标量属性,也就是说对于一点来说,压力沿任何方向的大小都是一样的。压力与其作用的面积相乘是表面力,表面力是有方向的,因为压力的作用面是有方向的。比如对于浸入水中的物体来说,只有作用在朝下的面的水压力才能产生向上的浮力,而朝上的面上作用的水压力都是向下的。由于要平衡作用于其内部的体积力,环绕微元体外表面的压力不能相同,而是有压差,正是这个压差产生的力与体积力之间平衡。
对于图 2-1所示的流体微团来说,如果在 x 方向上有图中所示向右的体积力的话,则微团右侧面的表面力一定要大于左侧面的力才能平衡。假定微团中心处的压力是 p,则其左侧面上的压力小于这个值,右侧面上的压力大于这个值。那如何将侧面上的压力用中心点处的压力表示出来呢?这就要用到一种力学中常用的方法──泰勒展开。在下一页的Tips中有针对泰勒展开的专门论述供读者参考,这里不再详述。应用泰勒展开,并忽略二阶以上小量后,左右侧面的压力可以分别写为
式中,\({\partial p}/{\partial x}\)表示了压力沿 x 方向的变化率,也称为沿 x 方向的压力梯度。可见,左右侧面上的压力都可以用微团中心处的压力及压力梯度表示。
现在已经得出了 x 方向的体积力和表面力,就可以列出力的平衡关系式了,即
类似地,也可以得到 y 方向和 z 方向的关系式,于是我们就得到了直角坐标系下分量形式的力平衡关系式如下:
式中,\({\partial p}/{\partial x}\),\({\partial p}/{\partial y}\) 和\({\partial p}/{\partial z}\) 表示了压力沿 3个方向的梯度。
根据梯度的定义:
可以将式(2.1)写成矢量形式如下:
式(2.1)和式(2.1a)就是静止的流体内部压力与体积力的关系,称为欧拉静平衡方程,是欧拉(Leonhard Euler,1707—1783)最先得出的。可以看到,当流体处于静止状态时,其内部的压力分布只与体积力相关,压力沿体积力作用方向增加。在重力场中下层流体的压力比上层的高,在离心力场中旋转半径大的地方的流体压力比旋转半径小的地方的大。这也可以这样理解:在重力场中上层流体的重量全靠下层流体来支撑,在离心力场中内层流体的向心力全靠外层流体提供。
2.2 重力作用下流体内部的压力分布
当静止或做匀速运动(内部无相对运动)的流体处于重力场中时,其内部的压力分布只受到重力的影响。对于图 2-2所示的处于重力场中的液体而言,根据式(2.1),若取垂直向上为坐标 z 的正向,则欧拉静平衡方程可以写为
当认为重力加速度与流体密度都为常数时,从这个公式可以积分得到液体内的压力公式:
式中,$p_0 $为液面处的大气压力;h为深度。
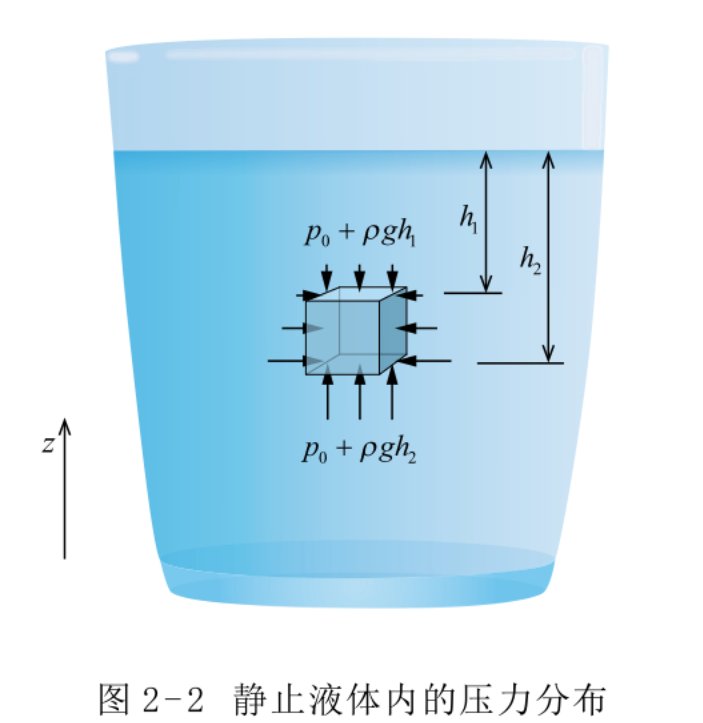
可见,液体内的压力只与大气压、液体密度和深度有关。根据该公式可以有如下的论述:形状不同而底面积相等的容器 ,内装有深度相等的水,虽然容器中水的重量不同,但水对底面的力却是相同的。例如图 2-3给出了四种不同形状的容器,水对底面的力都是相等的。这个结论最早是由帕斯卡(Blaise Pascal,1623—1662)提出来的,在当时是一个令人迷惑的现象,被人们称为“流体静力学悖论”。
2.3 惯性力作用下流体内部的压力分布
当流体做加减速运动时,只要加速度恒定,其内部就不会发生相对运动。这时如果与流体一起运动,则可以把加速度转化为惯性力,因此这一类问题也属于流体静力学问题。这类问题只有两种:即沿直线的恒加速运动和围绕某一中心的恒速转动。图 2-4表示了这两种情况下流体内部微团上的压力分布,在这两种运动中,惯性力与重力同时作为体积力发生作用。计算中只要把这两个力进行矢量叠加,再应用欧拉静平衡方程进行求解就行了。
参考文献
1.我所理解的流体力学-王洪伟