[43] (CSP 集训) CSP-S 模拟 10

B.清扫

考虑从叶子节点往上推

首先可以发现的几个性质

• 子树内需要消除的数，要么通过子树根节点 “发送” 到上面（只经过子树内一个叶节点），要么通过自己的叶节点解决
• 对于子树内既不是根也不是叶节点的节点，节点上的值只能由这一支路的叶节点消除，所以如果他节点上的值和下面节点 “发送” 上来的值不相等时，无解

然后考虑怎么去计算子树根节点向上的 “发送” 数量

设这个数量为 \(k\)，子树各支路 “发送” 到子树根节点的数量总和为 \(s\)，子树根节点的权值为 \(a\)，可以发现

• 子树内解决会为 \(s\) 带来 \(-2\) 的贡献
• “发送” 出去会为 \(s\) 带来 \(-1\) 的贡献
• 无论何种操作，每次操作总会给 \(a\) 带来 \(-1\) 的贡献

因此：

\[k+2(a-k)=s \]

由此可以唯一确定 \(k\)，将这个值继续往上传即可

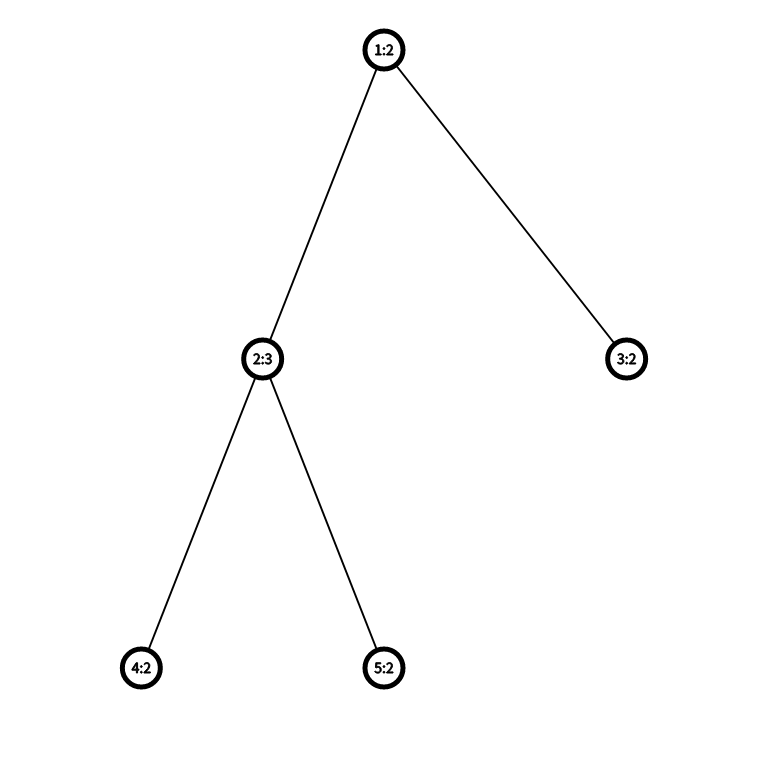
例图

这是一个 \(k=0\) 的图

需要注意的

• 由题有 \(0\le k\le a\)，否则无解
• 我们在上述式子中只判断了数量关系，但实际上，由于子树内必须要选择不同的叶子配对，因此可能会出现有叶子无法使用的情况，此时是无解的

这种情况的判断方式：\(s\) 个数的最大配对次数是 \(s/2\)，其次，每个点不能和自己匹配，所以有一个限制是 \(s-\max\)（其中 \(\max\) 是子树传入的最大值），这两个值取 \(\min\)，然后和子树的值总和比较，小于说明有剩余，报告无解

• 注意 \(n=2\) 的情况需要特判

#include<bits/stdc++.h>
using namespace std;
int n;
int a[100001];
vector<int>e[100001];
int degree[100001];
bool flag=false;
int dfs(int now,int last){
//	cout<<"dfs "<<now<<" "<<last<<endl;int res=0,cnt=0,maxn=0;for(int i:e[now]){if(i!=last){cnt++;int r=dfs(i,now);res+=r;maxn=max(maxn,r);if(flag) return 0;}}if(cnt==0){return a[now];}if(cnt==1){if(res!=a[now]){flag=true;return 0;}return res;}if(res<a[now] or res>2*a[now]){flag=true;return 0;}if(min(res/2,res-maxn)<res-a[now]){flag=true;return 0;} return 2*a[now]-res;
}
int main(){freopen("tree.in","r",stdin);freopen("tree.out","w",stdout);
//	freopen("b.in","r",stdin);scanf("%d",&n);for(int i=1;i<=n;++i){scanf("%d",&a[i]);}if(n==2){cout<<(a[1]==a[2]?"YES":"NO")<<'\n';return 0;}for(int i=1;i<=n-1;++i){int x,y;scanf("%d %d",&x,&y);e[x].push_back(y);e[y].push_back(x);degree[x]++;degree[y]++;}for(int i=1;i<=n;++i){
//		cout<<i<<" "<<degree[i]<<"::"<<endl;if(degree[i]!=1){if(dfs(i,0)){flag=true;}break;}}cout<<(flag?"NO":"YES");
}