一、特殊的矩阵

1、实对称矩阵

定义：都是实数，且

性质： 

（1）可以用特征值来求A的大小

（2）可以得到A的秩

（3）必定可以相似对角化

运用：

与实对称矩阵A合同的矩阵B，必定是实对称矩阵，这一性质可以用来排除某些选项

2、对角矩阵

定义：只有主对角线上有元素的矩阵

性质：

（1）对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算，且结果仍为对角阵

运用：

（1）特征值，秩

（2）证明A，B相似的中介

3、正定矩阵

定义：二次型，恒有，则称实对称矩阵A为正定矩阵

n阶正定矩阵的充分必要条件：

（1）A的正惯性指数是n

（2）A与E合同

（3）特征值均为正数

（4）各阶顺序主子式均大于0

必要条件：

（1）

（2）

4、零矩阵

定义：所有元素均为0

特殊的性质：

（1）若， 则。这是错误的！逆命题也是不对的。

（2）若 ，则B可逆。是错误的！

（3）若存在非零解，则A的秩小于n

5、可逆矩阵

（1）

（2）

如果A可逆，则Ax = 0 ，存在非零解

6、正交矩阵

（1）

（2）

（3）

二、特殊矩阵关系

1、相似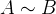

（1）

（2）  可用来判断A，B是否相似

2、合同

（1）正、负惯性指数相同

（2） 与 有相同的规范型

​​​​​​​